Вдохновленный профессором Вильдбергером в его серии лекций по линейной алгебре , я намереваюсь реализовать его математические идеи с помощью Flash. Мы не будем углубляться в математические манипуляции с матрицами через линейную алгебру: только через векторы. Это понимание, хотя и ослабляет элегантность линейной алгебры, достаточно, чтобы открыть нам некоторые интересные возможности манипулирования матрицей 2×2. В частности, мы будем использовать его для применения различных эффектов сдвига, перекоса, переворачивания и масштабирования к изображениям во время выполнения.
Окончательный результат предварительного просмотра
Давайте посмотрим на конечный результат, к которому мы будем стремиться. Нажмите четыре клавиши со стрелками — вверх, вниз, влево, вправо — чтобы увидеть некоторые эффекты, которые мы можем достичь с помощью аффинных преобразований.
Если вы используете только левую и правую клавиши со стрелками, рыба, кажется, плавает в псевдо-3D изометрическом пространстве.
Шаг 1: Различные координатные пространства
Графика рисуется на координатных пространствах. Поэтому для того, чтобы манипулировать ими, особенно для перевода, вращения, масштабирования, отражения и перекоса графики, очень важно, чтобы мы понимали координатные пространства. Обычно мы используем не одно, а несколько координатных пространств в одном проекте — это верно не только для дизайнеров, использующих Flash IDE, но и для программистов, пишущих ActionScript.
В Flash IDE это происходит всякий раз, когда вы конвертируете свои рисунки в символы MovieClip: каждый символ имеет свое происхождение.
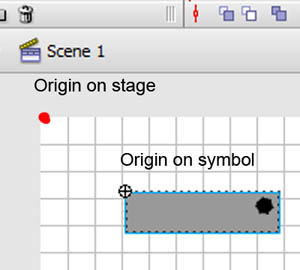
На изображении выше показано начало координатного пространства сцены (красная точка) и координатного пространства символа (точка регистрации, помеченная перекрестием). Чтобы узнать, в каком пространстве вы находитесь в данный момент, посмотрите на полосу под временной шкалой Flash IDE, как показано на рисунке ниже.
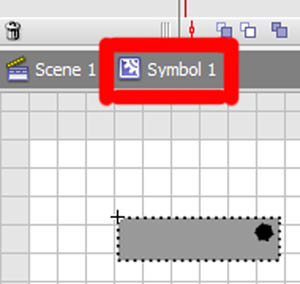
(Я использую Flash CS3, поэтому его расположение может различаться для CS4 и CS5.) Я хочу подчеркнуть наличие различных координатных пространств и тот факт, что вы уже знакомы с их использованием.
Шаг 2: Обоснование
Теперь есть веская причина для этого. Мы можем использовать одно координатное пространство как ссылку для изменения другого координатного пространства. Это может звучать чуждо, поэтому я включил презентацию Flash ниже, чтобы облегчить мое объяснение. Нажмите и перетащите красные стрелки. Поиграй с этим.
На заднем плане синяя сетка, а на переднем плане красная сетка. Синие и красные стрелки изначально выровнены вдоль оси x и y пространства координат Flash, центр которого смещен к середине сцены. Синяя сетка является эталонной сеткой; линии сетки не изменятся при взаимодействии с красными стрелками. Красная сетка, с другой стороны, может быть переориентирована и масштабирована путем перетаскивания красных стрелок.
Обратите внимание, что стрелки также указывают на важное свойство этих сеток. Они указывают понятие единицы x и единицы y на их соответствующей сетке. На красной сетке есть две красные стрелки. Каждый из них указывает длину одной единицы по оси X и оси Y. Они также определяют ориентацию координатного пространства. Давайте возьмем красную стрелку, направленную вдоль оси x, и увеличим ее вдвое по сравнению с исходной стрелкой (показана синим цветом). Обратите внимание на следующие изображения.
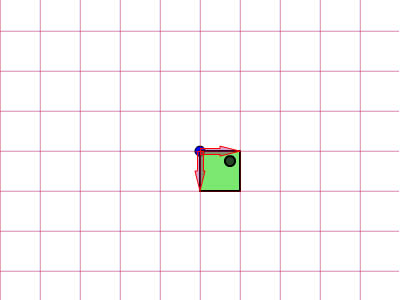
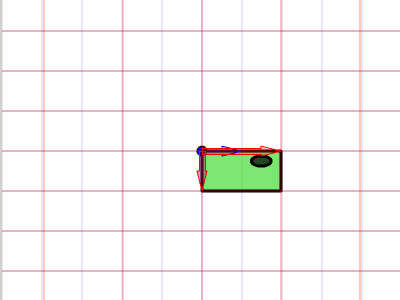
Мы видим, что изображение (зеленое поле), нарисованное на красной сетке, теперь растянуто по горизонтали, потому что эта красная сетка, на которой оно нарисовано, теперь в два раза шире. Пункт, который я пытаюсь сделать, довольно прост: вы можете использовать одно координатное пространство в качестве основы для изменения другого координатного пространства.
Шаг 3: аффинное координатное пространство
Так что же такое «аффинное координатное пространство»? Ну, я уверен, что вы достаточно осторожны, чтобы заметить, что эти координатные пространства нарисованы с использованием параллельных сеток. Давайте возьмем, например, красное аффинное пространство: нет никакой гарантии, что и ось x, и ось y всегда перпендикулярны друг другу, но будьте уверены, что как бы вы ни пытались настроить стрелки, вы никогда не достигнете такого случая как ниже.
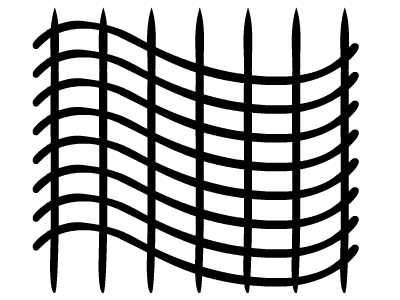
Это координатное пространство не является аффинным координатным пространством.
На самом деле оси X и Y обычно относятся к декартовому координатному пространству, как показано ниже.

Обратите внимание, что горизонтальные и вертикальные сетки перпендикулярны друг другу. Декартово является типом аффинного координатного пространства, но мы можем преобразовать его в другие аффинные пространства, как нам нравится. Горизонтальные и вертикальные сетки не обязательно должны быть перпендикулярны друг другу.

Пример аффинного координатного пространства

Еще один пример аффинного координатного пространства
Шаг 4: аффинные преобразования
Как вы уже догадались, аффинными преобразованиями являются перевод, масштабирование, отражение, наклон и вращение.

Оригинальное аффинное пространство
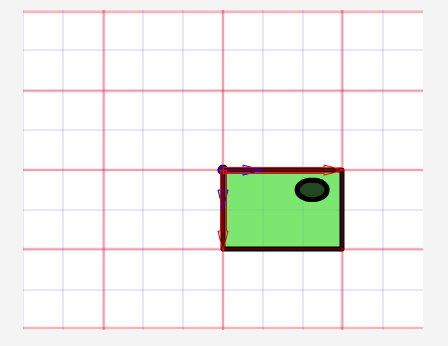
Масштабируемое аффинное пространство
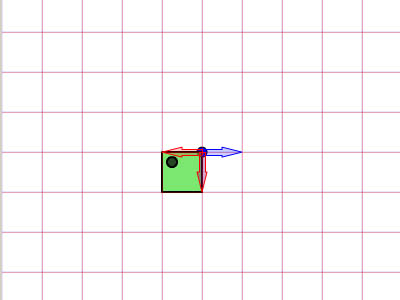
Отраженное аффинное пространство
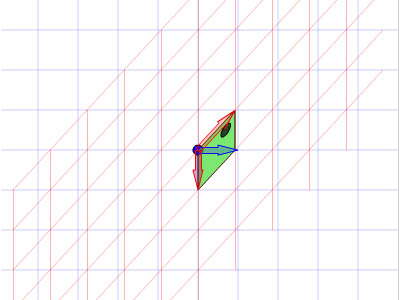
Перекошенное аффинное пространство
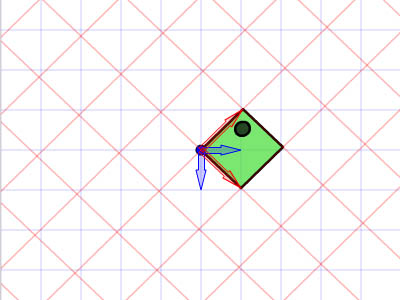
Вращенное и масштабированное аффинное пространство
Излишне говорить, что физические свойства, такие как x, y, scaleX, scaleY и rotation зависят от пространства. Когда мы обращаемся к этим свойствам, мы фактически преобразовываем аффинные координаты.
Шаг 5: Понимание матрицы
Я надеюсь, что изображения, показанные выше, достаточно ясны, чтобы развить идею. Это связано с тем, что для программиста, работающего с FlashDevelop, мы не увидим те сетки, которые Flash IDE удобно отображает для дизайнеров. Все это должно жить в вашей голове.
Помимо представления этих сеток, нам также необходимо заручиться поддержкой класса Matrix . Таким образом, важно иметь математическое понимание матриц, поэтому мы рассмотрим операции с матрицами здесь: сложение и умножение.
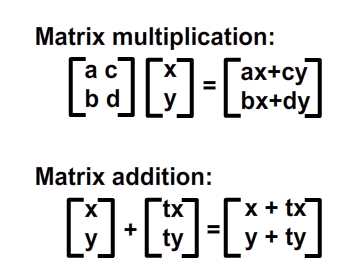
Шаг 6: Геометрический смысл добавления матрицы
Матричные операции соответствуют значениям геометрически. Другими словами, вы можете представить, что они значат на графике. Давайте предположим, что у нас есть четыре точки в нашем координатном пространстве, и мы хотели бы переместить их в набор новых местоположений. Это можно сделать с помощью сложения матриц. Проверьте изображение ниже.
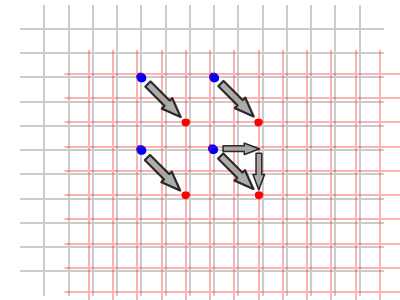
Как видите, мы на самом деле смещаем все локальное координатное пространство (красные сетки), где эти четыре точки нарисованы. Обозначение для выполнения этих операций, как показано ниже:
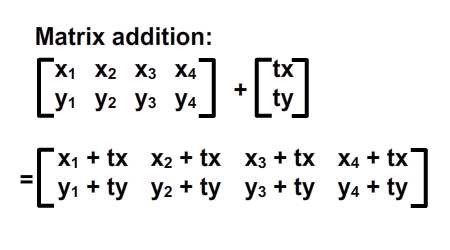
Мы также можем видеть, что этот сдвиг действительно может быть представлен с помощью вектора (tx, ty). Давайте дифференцируем векторы и статические точки в координатных пространствах, используя скобки и квадратные скобки. Я переписал их на изображении ниже.
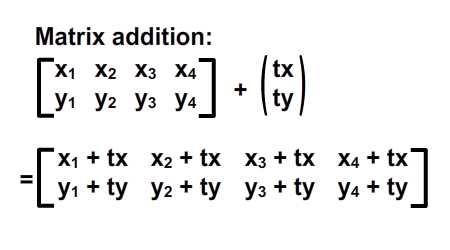
Шаг 7: Реализация ActionScript
Вот простая реализация добавления матрицы. Проверьте комментарии:
|
01
02
03
04
05
06
07
08
09
10
11
12
|
public class Addition extends Sprite
{
public function Addition()
{
var m:Matrix = new Matrix();
m.tx = stage.stageWidth * 0.5;
m.ty = stage.stageHeight * 0.5;
var d:DottedBox = new DottedBox();
addChild(d);
d.transform.matrix = m;
}
}
|
Шаг 8: Геометрический смысл умножения матриц
Умножение матриц несколько сложнее, чем сложение матриц, но профессор Вильдбергер элегантно разбил его на эту простую интерпретацию. Я смиренно попытаюсь повторить его объяснение. Для тех, кто хотел бы углубиться в понимание линейной алгебры, которая приводит к этому, ознакомьтесь с серией лекций профессора.
Давайте начнем с рассмотрения случая единичной матрицы, I.
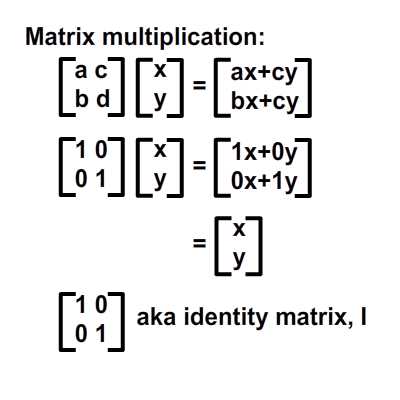
Из изображения выше мы знаем, что умножение произвольной матрицы A на единичную матрицу I всегда будет производить A. Вот аналогия: 6 x 1 = 6; единичная матрица сравнивается с числом 1 в этом умножении.
В качестве альтернативы мы можем записать результат в следующем векторном формате, что значительно упростит нашу интерпретацию:
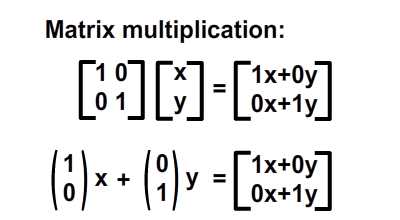
Геометрическая интерпретация этой формулы показана на рисунке ниже.
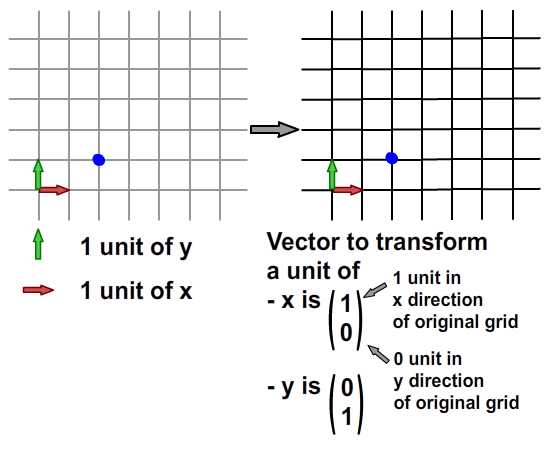
Из декартовой сетки (левая сетка) мы видим, что синяя точка расположена в (2, 1). Теперь, если мы должны были преобразовать эту исходную сетку из x и y в новую сетку (правую сетку) в соответствии с набором векторов (ниже правой сетки), синяя точка будет перемещена в (2, 1) на новой сетке — но когда мы отображаем это обратно в исходную сетку, это та же точка, что и раньше.
Поскольку мы преобразовываем исходную сетку в другую сетку, которая имеет те же векторы для x и y, мы не видим никакой разницы. Фактически, изменения x и y в этом преобразовании равны нулю. Это то, что он имел в виду под матрицей тождества с геометрической точки зрения.
Однако, если мы попытаемся выполнить отображение, используя другие преобразования, мы увидим некоторую разницу. Я знаю, что это был не самый показательный пример, поэтому давайте перейдем к другому примеру.
Шаг 9: масштабирование по X
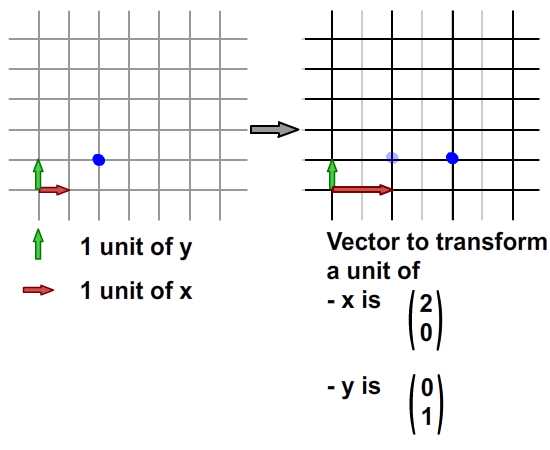
Изображение выше демонстрирует масштабирование координатного пространства. Проверьте вектор x в преобразованном координатном пространстве: одна единица преобразованного x составляет две единицы исходного x. В преобразованном координатном пространстве координата синей точки остается неподвижной (2, 1). Однако, если вы попытаетесь отобразить эту координату из преобразованной сетки в исходную сетку, это ( 4 , 1).
Вся эта идея запечатлена на изображении выше. Как насчет формулы? Результат должен быть последовательным; давайте проверим это.
Я уверен, что вы помните эти формулы. Теперь я добавил их соответствующие значения.
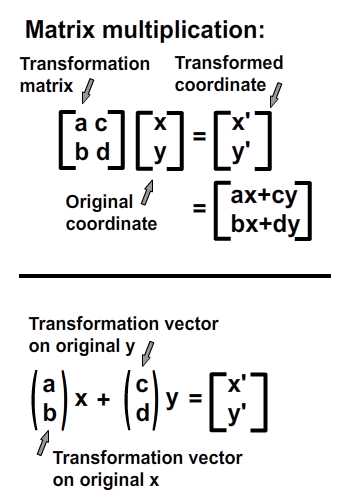
Теперь, чтобы проверить числовой результат нашего примера масштабирования.
- Исходная координата: (2, 1)
- Вектор на преобразованной оси X: (2, 0)
- Вектор на преобразованной оси Y: (0, 1)
- Ожидаемый результат: (2 * 2 + 0 * 1, 0 * 2 + 1 * 1) = (4, 1)
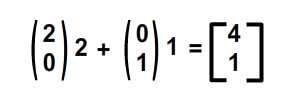
Они согласны друг с другом! Теперь мы можем с радостью применить эту идею к другим преобразованиям. Но перед этим реализация ActionScript.
Шаг 10: Реализация ActionScript
Проверьте реализацию ActionScript (и полученный SWF) ниже. Обратите внимание, что одно из перекрывающихся полей растягивается вдоль x по шкале 2. Я выделил важные значения. Эти значения будут настроены на последующих этапах для представления различных преобразований.
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
|
public class Multiplication extends Sprite
{
public function Multiplication()
{
var ref:DottedBox = new DottedBox();
addChild(ref);
var m:Matrix = new Matrix();
m.tx = stage.stageWidth * 0.5;
m.ty = stage.stageHeight * 0.5;
ma = 2;
mb = 0;
var d:DottedBox = new DottedBox();
addChild(d);
d.transform.matrix = m //apply the matrix onto our graphic
}
}
|
Шаг 11: Масштабирование X и Y
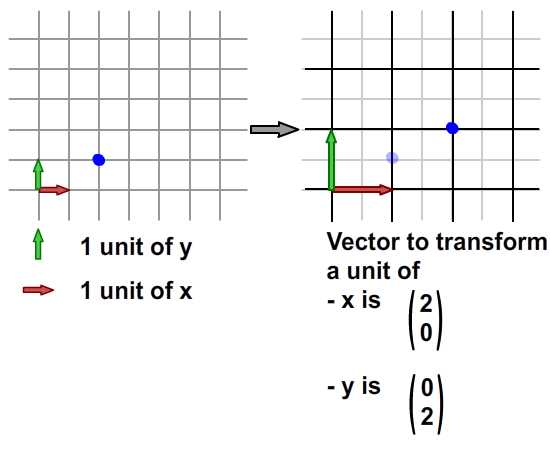
Здесь мы масштабировали сетку в два раза по осям X и Y. Синяя точка находится в (2, 1) в исходной сетке до преобразования и (4, 2) в исходной сетке после преобразования. (Конечно, это все еще в (2, 1) в новой сетке после преобразования.)
И подтвердить результат численно …
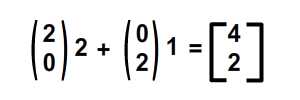
… они снова совпадают! Чтобы увидеть это в реализации ActionScript, просто измените значение md с 1 на 2.
(Обратите внимание, что направление растяжения от y направлено вниз, а не вверх, потому что y увеличивается во Flash вниз, но вверх в нормальном декартовом пространстве координат, которое я использовал на диаграмме.)
Шаг 12: Отражение
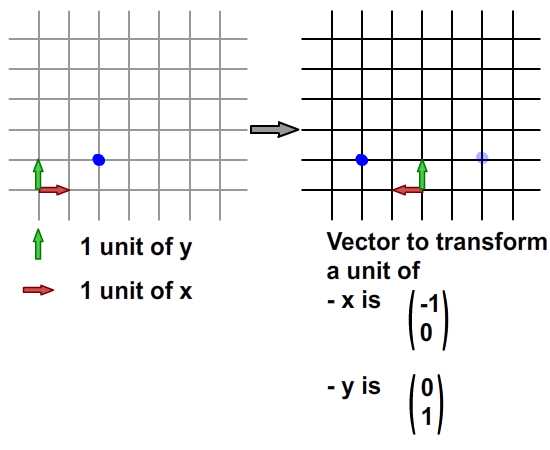
Здесь мы отразили сетку вдоль оси x, используя эти два вектора, поэтому положение синей точки в исходной сетке изменяется с (2, 1) на (-2, 1). Численный расчет выглядит следующим образом:
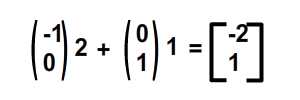
Реализация ActionScript такая же, как и раньше, но вместо этого используются следующие значения: ma = -1, mb = 0 для представления вектора для преобразования x и: mc = 0 and m. d = 1 mc = 0 and m. d = 1 для представления вектора для преобразования y.
Далее, как насчет одновременного отражения по x и y? Проверьте изображение ниже.
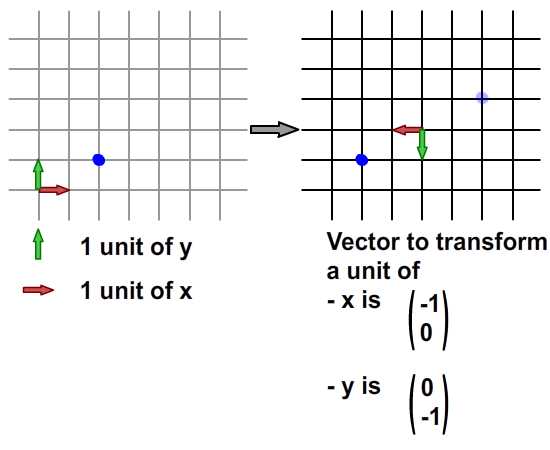
Кроме того, численно вычислено на изображении ниже.
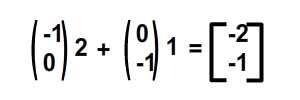
Для реализации ActionScript … я уверен, что вы знаете значения, которые нужно поместить в матрицу. ma = -1, mb = 0 для представления вектора для преобразования x; mc = 0 and m. d = -1 mc = 0 and m. d = -1 для представления вектора для преобразования y. Я включил окончательный SWF ниже.
Шаг 13: перекос и сдвиг
Перекос идет с небольшим удовольствием. Для случая изображения ниже, у преобразованной сетки была переориентирована и масштабирована ось X. Сравните красные стрелки в обеих сетках ниже: они разные, но ось Y остается неизменной.
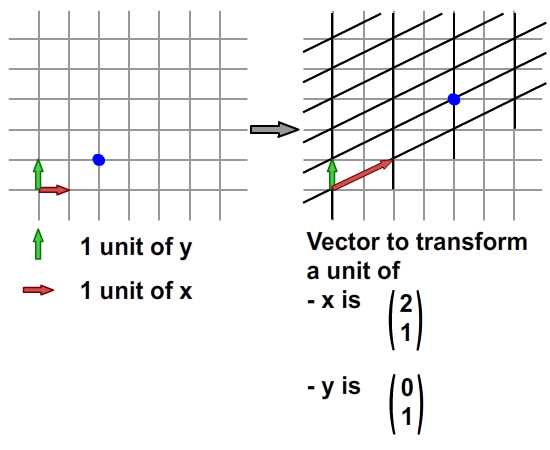
угловое смещение
Визуально кажется, что искажение происходит вдоль y-направления. Это правда, потому что наша преобразованная ось X теперь имеет Y-компонент в своем векторе.
Численно это то, что происходит …
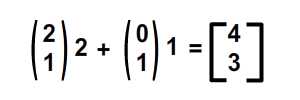
С точки зрения реализации, я перечислил твики ниже.
-
ma = 2 -
mb = 1 -
mc = 0 -
md = 1
Я уверен, что в этот момент вы хотели бы попробовать что-то самостоятельно, так что дерзайте
- ориентация преобразованной оси Y при сохранении оси X
- ориентация обеих осей в целом
Я включил выход Flash для обоих случаев, как показано ниже. Для читателей, которым нужна помощь с этими значениями, посмотрите Multiplication_final.as в исходной загрузке .
Шаг 14: Вращение
Я считаю вращение подмножеством перекоса. Единственное отличие состоит в том, что при вращении сохраняется величина единицы как по оси x, так и по оси y, а также перпендикулярность между двумя осями.
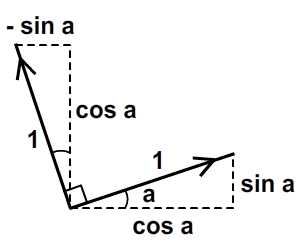
ActionScript фактически предоставляет метод в классе Matrix , rotate() , для этого. Но давайте все равно пройдем через это.
Теперь мы не хотим изменять величину длины единицы в x и y от исходной сетки; просто чтобы изменить ориентацию каждого. Мы можем использовать тригонометрию, чтобы получить результат, показанный на рисунке выше. При заданном угле поворота a мы получим желаемый результат, используя векторы (cos a, sin a) для оси x и (-sin a, cos a) для оси y. Величина для каждой новой оси все равно будет составлять одну единицу, но каждая ось будет находиться под углом а по сравнению с оригиналами.
Для реализации Actionscript, предполагая, что угол a равен 45 градусам (то есть 0,25 * Pi радиан), просто измените значения матрицы следующим образом:
|
1
2
3
|
var a:Number = 0.25*Math.PI
ma = Math.cos(a);
mb = Math.sin(a);
|
Полный источник может быть указан в Multiplication_final.as .
Шаг 15: Применение
Наличие векторной интерпретации матрицы 2×2 открывает нам пространство для исследования. Его применение для манипулирования растровыми изображениями ( BitmapData, LineBitmapStyle, LineGradientStyle и т. Д.) Широко распространено, но я думаю, что я BitmapData, LineBitmapStyle, LineGradientStyle это для другого урока. В случае этой статьи мы попытаемся исказить наш спрайт во время выполнения, чтобы он выглядел так, как будто он фактически переворачивается в 3D.

Вид псевдо-3D изометрического мира
Из изображения выше мы видим, что в мире с изометрической проекцией любой «стоящий» рисунок сохраняет свой вектор оси Y неизменным, а вектор оси X вращается. Обратите внимание, что единица длины для осей x и y не изменяется — другими словами, не должно происходить масштабирование по любой оси, только вращение вокруг оси x.
Вот пример этой идеи во Flash. Нажмите в любом месте на сцене и начните перетаскивать, чтобы увидеть рыбу. Отпустите, чтобы остановить ваше взаимодействие.
Вот важный фрагмент ActionScript. Я выделил важные линии, которые обрабатывают вращение оси X. Вы также можете обратиться к FakeIso.as .
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
private var f1:Fish, m:Matrix;
private var disp:Point;
private var axisX:Point, axisY:Point;
public function FakeIso() {
disp = new Point(stage.stageWidth * 0.5, stage.stageHeight * 0.5);
m = new Matrix();
m.tx = disp.x;
f1 = new Fish();
f1.transform.matrix = m;
axisX = new Point(1, 0);
axisY = new Point(0, 1);
stage.addEventListener(MouseEvent.MOUSE_DOWN, start);
stage.addEventListener(MouseEvent.MOUSE_UP, end);
}
private function start(e:MouseEvent):void {
f1.addEventListener(Event.ENTER_FRAME, update);
}
private function end(e:MouseEvent):void {
f1.removeEventListener(Event.ENTER_FRAME, update);
}
private function update(e:Event):void {
axisX.setTo(mouseX — f1.x, mouseY — f1.y);
axisX.normalize(1);
apply2Matrix();
}
private function apply2Matrix ():void {
m.setTo(axisX.x, axisX.y, axisY.x, axisY.y, disp.x, disp.y);
f1.transform.matrix = m;
}
|
Здесь я использовал класс Point для хранения векторов.
Шаг 16: добавь управление клавиатурой
На этом шаге мы попытаемся добавить элементы управления клавиатурой. Местоположение рыбы будет обновляться в соответствии с ее скоростью, velo . Мы также определим пошаговые шаги для положительного (по часовой стрелке) и отрицательного (против часовой стрелки) вращения.
|
1
2
3
4
|
velo = new Point(1, 0);
axisY = new Point(0, 1);
delta_positive = new Matrix();
delta_negative = new Matrix();
|
После нажатия клавиши velo будет вращаться:
|
1
2
3
4
5
6
7
8
|
private function keyUp(e:KeyboardEvent):void {
if (e.keyCode == Keyboard.LEFT) {
velo = delta_negative.transformPoint(velo) //rotate velo counter-clockwise
}
else if (e.keyCode == Keyboard.RIGHT) {
velo = delta_positive.transformPoint(velo) //rotate velo clockwise
}
}
|
Теперь для каждого кадра мы попытаемся раскрасить лицевую сторону рыбы, а также наклонить рыбу. Если скорость, velo , имеет величину больше 1, и мы применим ее к матрице рыбы, m , мы также получим эффект масштабирования — поэтому, чтобы исключить эту возможность, мы нормализуем скорость, а затем применим только это к матрице рыбы.
|
01
02
03
04
05
06
07
08
09
10
11
|
private function update(e:Event):void {
var front_side:Boolean = velo.x > 0 //checking for the front side of fish
if (front_side) { f1.colorBody(0x002233,0.5) } //color the front side of fish
else f1.colorBody(0xFFFFFF,0.5) //white applied to back side of fish
disp = disp.add(velo);
var velo_norm:Point = velo.clone();
velo_norm.normalize(1);
m.setTo(velo_norm.x, velo_norm.y, axisY.x, axisY.y, disp.x, disp.y);
f1.transform.matrix = m;
}
|
Шаг 17: Твоя рыба
Нажмите на сцену, затем нажмите левую и правую клавиши со стрелками, чтобы увидеть, как рыба меняет направление.
Шаг 18: еще одно управление с клавиатуры
Чтобы оживить ситуацию, давайте позволим также управлять вектором оси Y.
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
|
private function keyUp(e:KeyboardEvent):void {
if (e.keyCode == Keyboard.LEFT) {
velo = delta_negative.transformPoint(velo)
}
else if (e.keyCode == Keyboard.RIGHT) {
velo = delta_positive.transformPoint(velo)
}
if (e.keyCode == Keyboard.UP) {
axisY = delta_negative.transformPoint(axisY)
}
else if (e.keyCode == Keyboard.DOWN) {
axisY = delta_positive.transformPoint(axisY)
}
}
|
Также, чтобы определить переднюю сторону рыбы, теперь нам нужно включить ось Y. Вот код для этого:
|
1
2
3
|
var front_side:Boolean = velo.x * axisY.y > 0
if (front_side) { f1.colorBody(0x002233,0.5) }
else f1.colorBody(0xFFFFFF,0.5)
|
Шаг 19: Ваша необычная рыба
Ну, для некоторых результат управления обеими осями может показаться немного запутанным, но суть в том, что теперь вы можете наклонить свою рыбу, перевести ее, отразить и даже повернуть! Попробуйте комбинации вверх + влево, вверх + вправо, вниз + влево, вниз + вправо.
Также посмотрите, сможете ли вы сохранить «переднюю» сторону рыбы (рыба будет серой). Подсказка: постоянно нажимайте вверх, затем влево, затем вниз, затем вправо. Вы делаете вращение!
Вывод
Я надеюсь, что после прочтения этой статьи вы найдете математику матриц ценным активом для своих проектов. Я надеюсь написать немного больше о приложениях матрицы 2×2 в небольших Matrix3d Быстрые советы» из этой статьи, а также о Matrix3d который необходим для 3D-манипуляций. Спасибо за прочитанное, Терима Касых.