Так! Давайте поговорим о математике, потому что это весело. Мы будем использовать Python для этого, потому что нам не нужно его компилировать, это просто и полезно в проектах моделирования, таких как Micropolis.
Давайте сначала разберемся с некоторыми вещами. Python легко запустить:
$ python
Python 2.5.1 (r251:54863, May 18 2007, 16:56:43)
[GCC 3.4.4 (cygming special, gdc 0.12, using dmd 0.125)] on cygwin
Type "help", "copyright", "credits" or
"license" for more information.
>>>
Выход из Python также прост: CTRL-D делает свое дело.
Мы будем использовать разные шрифты для отображения вывода системы и ввода пользователя. Монотипический шрифт — это компьютерный текст; мы будем использовать серый фон, чтобы показать пользовательский ввод. Для специальных символов (например, CTRL-D) мы будем использовать курсив с серым фоном. Таким образом, взаимодействие выше будет:
$ python
Python 2.5.1 (r251:54863, May 18 2007, 16:56:43)
[GCC 3.4.4 (cygming special, gdc 0.12, using dmd 0.125)] on cygwin
Type "help", "copyright", "credits" or
"license" for more information.
>>> "hello" 'hello' >>> [CTRL-D] $
Хорошо, это было весело. («Правда?») Теперь мы тоже будем делать некоторые вещи с текстовым редактором, потому что мы хотим перезагрузить вещи вместо того, чтобы перепечатывать их, так что мы могли бы также открыть редактор где-нибудь.
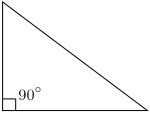
Треугольник это фигура , которая имеет три стороны, не так ли? Это довольно простые вещи. Есть нечто, называемое «прямоугольным треугольником», в котором есть одна особенность: один из углов всегда девяносто градусов. (Угол в девяносто градусов — это тип угла, который имеют квадраты для простого объяснения. Если вам интересно, более сложное объяснение состоит в том, что круг, разделенный на четыре равные части, будет иметь четыре прямых угла, пересекающихся в его центре. Если это вас смутило, вернитесь к квадрату. Это проще.)
Прямоугольный треугольник удивительно, удивительно полезен. Однако, прежде чем мы сможем научиться использовать его, нам нужно узнать немного больше об этом.
Для простоты, давайте посмотрим на треугольник и обозначим его части:
Давайте переименуем вертикальную линию в сегмент «А». Линия внизу, давайте назовем это «B». «Гипотенуза» — кстати, правильное название для этого сегмента — это то, что мы будем называть «С».
Nu! +1 Давайте поиграем с этим треугольником. Помните, что эта гипотенуза — линия «С» — имеет определенную длину . Всегда. Эта длина зависит от длины A и B, но если вы знаете длину любых двух сторон прямоугольного треугольника, вы всегда можете определить длину третьей. (На самом деле, вы также можете сказать, каковы конкретные углы, но это не важно для нас прямо сейчас.)
То, как мы это делаем, — это так называемая «теорема Пифагора». Пифагор был греческим математиком, который жил примерно за пятьсот лет до рождения Христа (т. Е. В начале нашей эры). Мы мало знаем о нем, потому что его труды не сохранились, но каждый знает что-то о нем, потому что теорема Пифагора является одной из самых полезных математических формул, которыми располагает человечество. Он, возможно, даже не придумал это, но он получает кредит за это. (Возможно, «кое-что, что мы знаем» о Пифагоре, заключается в том, что теорема Пифагора названа в его честь … это не так уж и много, но последний раз, когда я проверял, это больше, чем я назвал в честь себя .)
Что за теорема? Ну, теорема это то, что можно доказать. Достаточно просто, а? (На самом деле это немного сложнее, чем все остальное, но давайте не будем путать проблему больше, чем у нас уже есть.)
Вот что на самом деле говорит теорема Пифагора: «В любом прямоугольном треугольнике площадь квадрата, стороной которого является гипотенуза (сторона, противоположная прямому углу), равна сумме площадей квадратов, сторонами которых являются две ноги ( две стороны, которые встречаются под прямым углом). » Глядя на нашу диаграмму снова, C — гипотенуза, помните?
Поэтому, если мы говорим «A» и «B» — это длины сторон, которые они представляют, тогда мы всегда можем определить длину C следующим образом: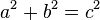
Захватывающие вещи, а? Давайте объясним все там. A, b и c представляют длины сторон, которые они представляют, причем c является стороной, противоположной прямому углу .
Маленькие верхние индексы называются экспонентами . Показатель степени — это способ сказать «это число умножается на себя X раз». Так что 4 2 — это то же самое, что и 4 * 4; 3 3 — это то же самое, что и 3 * 3 * 3. То, как c 2 показывается как результат, означает, что любое число, которое мы получаем от добавления 2 и b 2 , нам нужно определить «квадратный корень» — «4» в «4 2 » там наверху.
Итак … давайте пройдемся по этому немного, не так ли? Давайте посмотрим на наш треугольник и добавим несколько цифр. Давайте сделаем 3 и б 4. Это означает , что наше уравнение выглядит следующим образом : с = (квадратный корень) 3 * 3 + 4 * 4
Давайте начнем математизировать! (Да, я придумал это слово.) Во-первых, мы применяем наши показатели, поэтому формула выглядит следующим образом:
с = (квадратный корень) 9 + 16 - помня, что 3 2 = 3 * 3 = 9 и 4 2 = 4 * 4 = 16.
Теперь наш следующий шаг — это сложение, поэтому наша формула теперь выглядит так: c = (квадратный корень из) 25
Если вы помните что-нибудь о наших друзьях, экспонентах и их кузенах с квадратными корнями, то вы знаете, что 5 * 5 = 25, что означает, что c здесь равно 5.
Теперь мы рассмотрели теорему Пифагора в довольно болезненных деталях, но, надеюсь, вы понимаете это сейчас.
Мы начали с Python! Мы немедленно оставили это позади — это может быть хорошее время, чтобы вернуться к нему.
Итак, давайте напишем теорему Пифагора в виде функции, чтобы мы всегда могли определить c , учитывая a и b . (Мы могли бы сделать и другие вещи, такие как — с учетом c и a , определить b . Но давайте пока остановимся на этом.)
Давайте сначала сделаем простую вещь и используем числа, которые мы вставили раньше. Давайте получим Python c , если a и b равны 3 и 4 соответственно.
$ python
Python 2.5.1 (r251:54863, May 18 2007, 16:56:43)
[GCC 3.4.4 (cygming special, gdc 0.12, using dmd 0.125)] on cygwin
Type "help", "copyright", "credits" or
"license" for more information.
>>> import math >>> a=3 >>> b=4 >>> math.sqrt(math.pow(a,2)+math.pow(b,2)) 5.0 >>> [CTRL-D] $
Вау! Это именно тот результат, который мы хотели получить! Там есть несколько странных вещей: там «import math» делает «sqrt» — имя Python для функции, которая дает вам квадратный корень из числа, — и pow (который применяет экспоненты к числам), затем мы присваиваем a и b, затем мы … говорим python, что нужно вычислить квадратный корень от сложения квадратов a и b . (В конце концов, это теорема Пифагора!)
Однако много печатать приходится делать снова и снова, поэтому давайте обратимся к нашему удобному редактору денди и напишем метод, который сделает это за нас.
Откройте файл с именем «triangle.py» — со временем мы будем делать больше вещей с треугольниками. Мы будем создавать модуль под названием «треугольник», хранящийся в этом файле.
В этом файле нам понадобится следующий текст, большая часть которого будет выглядеть очень похоже на то, что мы только что видели выше:
import math
def hypotenuse(a, b):
return math.sqrt(math.pow(a,2)+math.pow(b,2))
Теперь мы можем использовать это так:
$ python
Python 2.5.1 (r251:54863, May 18 2007, 16:56:43)
[GCC 3.4.4 (cygming special, gdc 0.12, using dmd 0.125)] on cygwin
Type "help", "copyright", "credits" or
"license" for more information.
>>> import triangle >>> triangle.hypotenuse(3,4) 5.0 >>> [CTRL-D] $
Если мы хотим, мы можем играть с другими числами: попробуйте a = 4, b = 5! (Вы увидите, что результат равен 6.4031 или около того.) Не стесняйтесь вкладывать все, что вам нравится, и посмотрите, что вы получите.