Мы занимались рисованием кривых и нахождением их квадратичных и кубических корней , а также удобными приложениями для использования квадратичных корней в играх. Теперь, как и было обещано, мы рассмотрим приложения для поиска кубических корней, а также градиенты и нормали кривых, например, чтобы объекты отскакивали от искривленных поверхностей. Пошли!
пример
Давайте рассмотрим одно практическое использование этой математики:
В этой демонстрации «корабль» отскакивает от краев SWF и кривой. Желтая точка представляет собой ближайшую точку к кораблю, которая лежит на кривой. Вы можете настроить форму кривой, перетаскивая красные точки, и отрегулировать движение корабля с помощью клавиш со стрелками.
Шаг 1: Наименьшее расстояние до кривой
Давайте рассмотрим сценарий, в котором точка расположена вблизи квадратичной кривой. Как рассчитать кратчайшее расстояние между точкой и кривой?
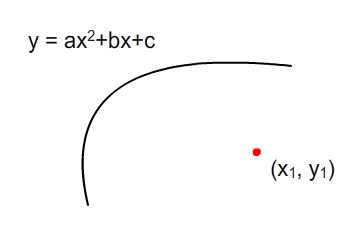
Что ж, начнем с теоремы Пифагора.
\ [
Пусть \ the \ point \ be \ (x_p, \ y_p) \\
и \ вызвать \ ближайшую \ точку \ на \ кривой \ (x_c, \ y_c) \\
Потом:\\
z ^ 2 = x ^ 2 + y ^ 2 \\
z ^ 2 = (x_c-x_p) ^ 2 + (y_c-y_p) ^ 2 \\
Дано \ y_c = ax_c ^ 2 + bx_c + c, \\
z ^ 2 = (x_c-x_p) ^ 2 + [(ax_c ^ 2 + bx_c + c) -y_p] ^ 2
\]
Вы можете видеть, что мы заменили \ (y_c \) квадратным уравнением. С первого взгляда видно, что наибольшая степень равна 4. Таким образом, мы имеем квартальное уравнение. Все, что нам нужно сделать, это найти минимальную точку в этом уравнении, чтобы дать нам кратчайшее расстояние от точки до квадратичной кривой.
Но перед этим нам нужно понять градиенты на кривой …
Шаг 2: градиент кривой
Прежде чем мы рассмотрим проблему минимизации квартального уравнения, давайте попробуем понять градиенты кривой. Прямая линия имеет только один градиент. Но градиент квадратичной кривой зависит от того, на какую точку кривой мы ссылаемся. Проверьте презентацию Flash ниже:
Перетащите красные точки вокруг, чтобы изменить квадратичную кривую. Вы также можете поиграть с ручкой ползунка, чтобы изменить положение синей точки вдоль x. Когда синяя точка изменится, изменится и градиент.
Шаг 3: градиент через исчисление
Вот где исчисление пригодится. Возможно, вы уже догадались, что дифференцирование квадратного уравнения даст вам градиент кривой.
\ [
f (x) = ax ^ 2 + bx + c \\
\ frac {df (x)} {dx} = 2ax + b
\]
Таким образом, \ (\ frac {df (x)} {dx} \) является градиентом квадратичной кривой и зависит от координаты \ (x \). Что ж, хорошо, у нас есть метод для обработки этого: diff1(x:Number) вернет значение после одного дифференцирования.
Чтобы нарисовать градиент, нам понадобится уравнение для представления линии \ (y = mx + c \). Координата синей точки \ ((x_p, y_p) \) будет подставлена в \ (x \) и \ (y \), а градиент линии, найденной путем дифференцирования, перейдет в \ (m \). Таким образом, y-пересечение прямой \ (c \) можно вычислить с помощью некоторой работы алгебры.
Проверьте AS3:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
|
var x:Number = s.value
var y:Number = quadratic_equation.fx_of(s.value)
point.x = x;
point.y = y;
/**
* y = mx + c;
* c = y — mx;
*/
var m:Number = quadratic_equation.diff1(x);
var c:Number = y — m * x;
graphics.clear();
graphics.lineStyle(1, 0xff0000);
graphics.moveTo(0, c);
graphics.lineTo(stage.stageWidth, m * stage.stageWidth + c);
|
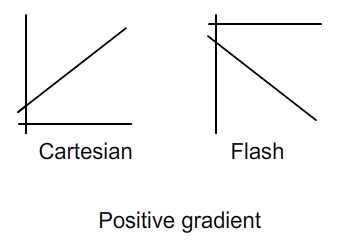
Шаг 4: Системы координат
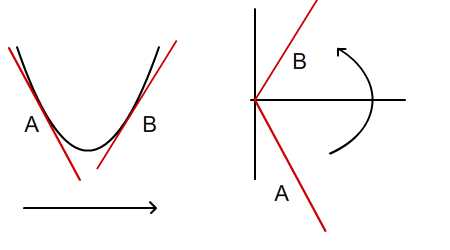
Всегда помните о перевернутой оси Y координатного пространства Flash, как показано на рисунке ниже. На первый взгляд, диаграмма справа может показаться отрицательным градиентом — но из-за перевернутой оси Y, это на самом деле положительный градиент.
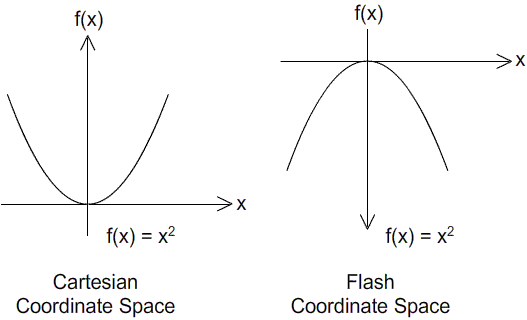
То же самое касается минимальной точки, как указано ниже. Из-за перевернутой оси y минимальная точка в декартовом координатном пространстве (в точке (0,0)) выглядит как максимум в координатном пространстве Flash. Но, ссылаясь на местоположение источника в координатном пространстве Flash относительно квадратичной кривой, это фактически минимальная точка.
Шаг 5: Скорость изменения градиента
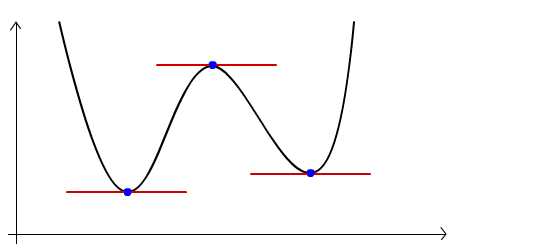
Теперь предположим, что я заинтересован в нахождении самой низкой точки на кривой — как мне действовать? Посмотрите на изображение ниже (обе фигуры находятся в одном координатном пространстве).
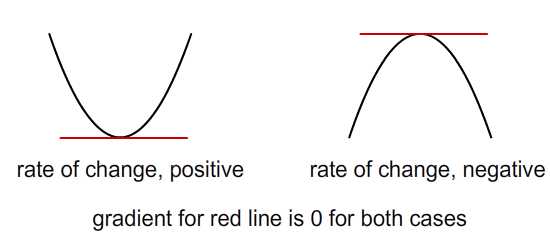
Чтобы получить минимальную точку, мы просто приравняем \ (\ frac {df (x)} {dx} = 0 \), поскольку по определению мы ищем точку, где градиент равен нулю. Но, как показано выше, оказывается, что точка максимума на кривой также удовлетворяет этому условию. Итак, как мы можем различать эти два случая?
Давайте попробуем дифференцирование второй степени. Это даст нам скорость изменения градиента.
\ [
\ frac {df (x)} {dx} = 2ax + b \\
\ frac {df ^ 2 (x)} {dx ^ 2} = 2a
\]
Я объясню со ссылкой на изображение ниже (нарисовано в декартовом координатном пространстве). Мы можем видеть, что при увеличении по оси X градиент меняется с отрицательного на положительный. Так что скорость изменения должна быть положительной величиной.
Мы также можем видеть, что когда \ (\ frac {df ^ 2 (x)} {dx ^ 2} \) положителен, на кривой есть минимальная точка. И наоборот, если показатель отрицательный, максимальная точка присутствует.
Шаг 6: Вернуться к проблеме
Теперь мы готовы решить проблему, представленную на шаге 1. Вспомните уравнение четвертого порядка (где наивысшая степень равна 4), к которому мы пришли:
\ [
z ^ 2 = (x_c-x_p) ^ 2 + [(ax_c ^ 2 + bx_c + c) -y_p] ^ 2
\]
То же уравнение квартики, построенное
Помните, нам интересно найти минимальную точку на этой кривой, потому что соответствующей точкой на исходной квадратичной кривой будет точка, которая находится на минимальном расстоянии от красной точки.
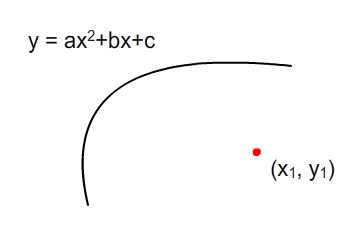
Итак, давайте дифференцируем функцию четверти, чтобы получить градиент этой кривой, а затем приравниваем градиент этой функции к нулю. Вы увидите, что градиент на самом деле является кубической функцией. Я отошлю заинтересованных читателей на страницу Вольфрама ; для этого урока я просто соберу результаты их алгебраической работы:
\ [
\ Гидроразрыва {d (г ^ 2)} {дх} =
2 (x_c-x_p) + 2 (ax_c ^ 2 + bx_c + c — y_p) (2ax_c + b) \\
\ frac {d (z ^ 2)} {dx} = 2a ^ 2 (x_c) ^ 3 + 3ab (x_c) ^ 2 + (b ^ 2 + 2ac-2ay_p + 1) (x_c) + (bc-by_p- x_p) \\
Приравнять \ градиент \ к \ 0 \\
\ Гидроразрыва {d (г ^ 2)} {дх} = 0 \\
2a ^ 2 (x_c) ^ 3 + 3AB (x_c) ^ 2 + (б ^ 2 + 2ac-2ay_p + 1) (x_c) + (BC-by_p-x_p) = 0 \\
Сравните \ с \ кубическим \ уравнением \\
Ах ^ 3 + BX ^ 2 + Сх + D = 0 \\
A = 2a ^ 2 \\
В = \\ 3AB
С = Ь ^ 2 + 2ac-2ay_p + 1 \\
D = BC-by_p-x_p
\]
Решите для корней этой (довольно грязной) кубической функции, и мы получим координаты трех синих точек, как указано выше.
Далее, как мы фильтруем наши результаты по минимальной точке? Напомним из предыдущего шага, что минимальная точка имеет скорость изменения, которая является положительной. Чтобы получить эту скорость изменения, дифференцируйте кубическую функцию, которая представляет градиент. Если скорость изменения для данной синей точки положительна, это одна из минимальных точек. Чтобы получить минимальный балл, тот, который нас интересует, выберите балл с наивысшей скоростью изменения.
Шаг 7: Пример вывода
Итак, вот пример реализации идеи, объясненной выше. Вы можете перетащить красные точки вокруг, чтобы настроить свою квадратичную кривую. Синяя точка также может быть перетащена. При перемещении синей точки желтая точка будет перемещена так, чтобы расстояние между синей и желтой точками было минимальным среди всех точек на кривой.
При взаимодействии с презентацией Flash могут быть случаи, когда сразу появляются три желтые точки. Два из них, заштрихованные, относятся к корням, полученным из расчета, но отклоненным, поскольку они не являются ближайшими точками на кривой к синей точке.
Шаг 8: Реализация ActionScript
Итак, вот реализация ActionScript выше. Вы можете найти полный скрипт в Demo2.as .
Прежде всего, нам нужно нарисовать квадратичную кривую. Обратите внимание, что матрица m2 будет указана для дальнейшего расчета.
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
private function redraw_quadratic_curve():void
{
var cmd:Vector.<int> = new Vector.<int>;
var coord:Vector.<Number> = new Vector.<Number>;
//redraw curve;
m1 = new Matrix3d(
curve_points[0].x * curve_points[0].x, curve_points[0].x, 1, 0,
curve_points[1].x * curve_points[1].x, curve_points[1].x, 1, 0,
curve_points[2].x * curve_points[2].x, curve_points[2].x, 1, 0,
0,0,0,1
);
m2 = new Matrix3d(
curve_points[0].y, 0, 0, 0,
curve_points[1].y, 0, 0, 0,
curve_points[2].y, 0, 0, 0,
0,0,0,1
)
m1.invert();
m2.append(m1);
quadratic_equation.define(m2.n11, m2.n21, m2.n31);
for (var i:int = 0; i < stage.stageWidth; i+=2)
{
if (i == 0) cmd.push(1);
else cmd.push(2);
coord.push(i, quadratic_equation.fx_of(i));
}
graphics.clear();
graphics.lineStyle(1);
graphics.drawPath(cmd, coord);
}
|
И вот тот, который реализует объясненную математическую концепцию. c1 относится к точке, случайно расположенной на сцене.
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
|
private function recalculate_distance():void
{
var a:Number = m2.n11;
var b:Number = m2.n21;
var c:Number = m2.n31;
/*f(x) = Ax^3 + Bx^2 +Cx + D
*/
var A:Number = 2*a*a
var B:Number = 3*b*a
var C:Number = b*b + 2*c*a — 2*a*c1.y +1
var D:Number = c * b — b * c1.y — c1.x
quartic_gradient = new EqCubic();
quartic_gradient.define(A, B, C, D);
quartic_gradient.calcRoots();
roots = quartic_gradient.roots_R;
var chosen:Number = roots[0];
if (!isNaN(roots[1]) && !isNaN(roots[2])) {
//calculate gradient and rate of gradient of all real roots
var quartic_rate:Vector.<Number> = new Vector.<Number>;
for (var i:int = 0; i < roots.length; i++)
{
if (!isNaN(roots[i])) quartic_rate.push(quartic_gradient.diff1(roots[i]));
else roots.splice(i, 1);
}
//select the root that will produce the shortest distance
for (var j:int = 1; j < roots.length; j++)
{
//the rate that corresponds with the root must be the highest positive value
//because that will correspond with the minimum point
if (quartic_rate[j] > quartic_rate[j — 1]) {
chosen = roots[j];
}
}
//position the extra roots in demo
position_extras();
}
else {
//remove the extra roots in demo
kill_extras();
}
intersec_points[0].x = chosen
intersec_points[0].y = quadratic_equation.fx_of(chosen);
}
|
Шаг 9: Пример: обнаружение столкновения
Давайте воспользуемся этой концепцией, чтобы обнаружить наложение между кругом и кривой.
Идея проста: если расстояние между синей точкой и желтой точкой меньше радиуса синей точки, мы имеем столкновение. Проверьте демо ниже. Интерактивные элементы — это красные точки (для управления кривой) и синяя точка. Если синяя точка сталкивается с кривой, она немного исчезнет.
Шаг 10: Реализация ActionScript
Ну, код довольно прост. Проверьте полный исходный код в CollisionDetection.as .
|
01
02
03
04
05
06
07
08
09
10
11
12
13
|
graphics.moveTo(intersec_points[0].x, intersec_points[0].y);
graphics.lineTo(c1.x, c1.y);
var distance:Number= Math2.Pythagoras(
intersec_points[0].x,
intersec_points[0].y,
c1.x,
c1.y)
if (distance < c1.radius) c1.alpha = 0.5;
else c1.alpha = 1.0;
t.text = distance.toPrecision(3);
|
Шаг 11: отскакивая от кривой
Итак, теперь, когда мы знаем, когда произойдет столкновение, давайте попробуем запрограммировать реакцию на столкновение. Как насчет отскока от поверхности? Проверьте презентацию Flash ниже.
Вы можете увидеть корабль (треугольной формы), окруженный кругом (полупрозрачный синий). Как только круг столкнется с кривой, корабль отскочит от поверхности.
Шаг 12: Управление кораблем
Вот код ActionScript для управления кораблем.
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
|
public function CollisionDetection2()
{
/**
* Instantiation of ship & its blue-ish circular area
*/
ship = new Triangle();
ship.x = Math.random() * stage.stageWidth;
ship.y = stage.stageHeight * 0.8;
c1 = new Circle(0x0000ff, 15);
c1.alpha = 0.2;
/**
* Ship’s velocity
*/
velo = new Vector2D(0, -1);
updateShip();
stage.addEventListener(KeyboardEvent.KEY_DOWN, handleKey);
stage.addEventListener(KeyboardEvent.KEY_UP, handleKey);
stage.addEventListener(Event.EXIT_FRAME, handleEnterFrame);
/**
* The curve and the calculations
*/
quadratic_equation = new EqQuadratic();
curve_points = new Vector.<Circle>;
populate(curve_points, 0xff0000, 3);
intersec_points = new Vector.<Circle>;
populate(intersec_points, 0xffff00, 3, false);
redraw_quadratic_curve();
}
private function handleKey(e:KeyboardEvent):void
{
if (e.type == «keyDown») {
if (e.keyCode == Keyboard.UP) isUp = true;
else if (e.keyCode == Keyboard.DOWN) isDown = true;
if (e.keyCode == Keyboard.LEFT) isLeft = true;
else if (e.keyCode == Keyboard.RIGHT) isRight = true;
}
if (e.type == «keyUp») {
if (e.keyCode == Keyboard.UP) isUp = false;
else if (e.keyCode == Keyboard.DOWN) isDown = false;
if (e.keyCode == Keyboard.LEFT) isLeft = false;
else if (e.keyCode == Keyboard.RIGHT) isRight = false;
}
}
private function handleEnterFrame(e:Event):void
{
/**
* Control the magnitude
*/
if (isUp) velo.setMagnitude(Math.min(velo.getMagnitude()+0.2, 3));
else if(isDown) velo.setMagnitude(Math.max(velo.getMagnitude()-0.2, 1));
/**
* Control the direction
*/
if (isRight) velo.setAngle(velo.getAngle() + 0.03);
else if (isLeft) velo.setAngle(velo.getAngle() — 0.03);
recalculate_distance();
if (distance < c1.radius) bounce();
updateShip();
}
/**
* Update ship’s position, orientation and it’s area (the blue-ish circle)
*/
private function updateShip():void {
ship.x += velo.x;
ship.y += velo.y;
ship.rotation = Math2.degreeOf(velo.getAngle());
c1.x = ship.x;
c1.y = ship.y;
if (ship.x > stage.stageWidth || ship.x < 0) velo.x *= -1;
if (ship.y > stage.stageHeight || ship.y < 0) velo.y *= -1;
}
|
Вы можете видеть, что элементы управления клавиатуры обновляют флаги, чтобы указывать, нажимаются ли клавиши влево, вверх, вправо или вниз. Эти флаги будут захвачены обработчиком событий enterframe и обновят величину и направление корабля.
Шаг 13: Расчет вектора отражения
Я уже рассмотрел вычисление вектора отражения вектора в этом посте . Здесь я просто расскажу, как получить вектор нормали из градиента.
\ [
\ Гидроразрыва {DF (х)} {дх} = градиент \\
линия \ градиент = \ frac {y} {x} \\
Предположим, что градиент = 0,5
у = 0,5 \\
х = 1 \\
Вектор \ of \ left \ normal =
\ begin {bmatrix} -1 \\ 0.5 \ end {bmatrix} \\
Вектор \ of \ right \ normal =
\ begin {bmatrix} 1 \\ — 0.5 \ end {bmatrix}
\]
Шаг 14: Реализация ActionScript
Таким образом, приведенный ниже код ActionScript будет реализовывать математическую концепцию, объясненную на предыдущем шаге. Проверьте выделенные строки:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
|
private function bounce():void
{
var gradient:Number = quadratic_equation.diff1(intersec_points[0].x);
var grad_vec:Vector2D = new Vector2D(1, gradient);
var left_norm:Vector2D = grad_vec.getNormal(false);
var right_norm:Vector2D = grad_vec.getNormal();
var chosen_vec:Vector2D;
if (velo.dotProduct(left_norm) > 0) chosen_vec = left_norm
else chosen_vec = right_norm
var chosen_unit:Vector2D = chosen_vec.normalise();
var proj:Number = velo.dotProduct(chosen_unit);
chosen_unit.scale(-2*proj);
velo = velo.add(chosen_unit);
}
|
Вывод
Ну, спасибо за ваше время! Если вы нашли это полезным или у вас есть какие-либо вопросы, оставляйте комментарии.