Дважды в месяц мы возвращаемся к любимым постам наших читателей из истории Activetuts +. Учебное пособие по ретроактивности этой недели, впервые опубликованное в апреле, представляет собой руководство по евклидовым векторам: что это такое, почему вы их используете и как реализовать их во Flash с AS3.
Евклидовы векторы — это объекты в геометрии с определенными свойствами, которые очень полезны для разработки игр. Их можно рассматривать как точки, но они также имеют величину и направление. Они представлены в виде стрелок, идущих от начальной точки к конечной точке, и именно так мы их нарисуем в этой статье.
Евклидовы векторы широко используются в математике и физике для многих вещей: они могут представлять скорость, ускорение и силы в физике или помочь доказать множество важных теорем в математике. В этом руководстве вы узнаете о евклидовых векторах и создадите класс, который вы сможете использовать в своих собственных проектах Flash.
Обратите внимание, что евклидовы векторы отличаются от векторного класса ActionScript , а также от векторного рисования .
Векторы можно использовать в среде Flash, чтобы помочь вам решать сложные задачи, которые в противном случае потребовали бы больших усилий, если бы они были выполнены без них. В этой статье вы узнаете, как использовать их во Flash, а также узнаете много интересных трюков с векторами.
Шаг 1: Декартовы координаты и координаты Флэша
Прежде чем переходить к векторам, давайте познакомимся с системой координат Flash. Вы, вероятно, знакомы с декартовой системой координат (даже если вы не знаете ее по имени):
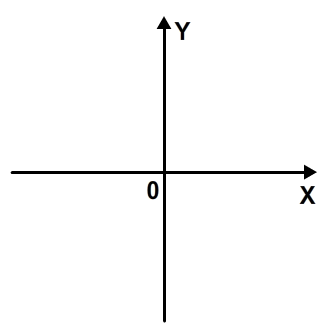
Система Flash очень похожа. Разница лишь в том, что ось Y перевернута:
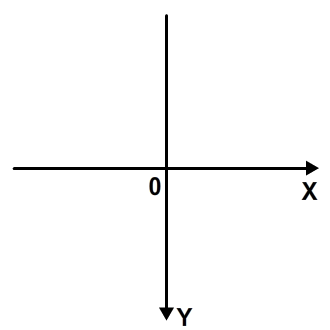
Когда мы начинаем работать с векторами во флэш-памяти, мы должны помнить об этом. Тем не менее, хорошие новости: эта другая система не имеет большого значения. Работа с векторами в нем будет в основном похожа на работу с векторами в декартовой системе.
Шаг 2: Определение вектора
Для целей данного урока мы определим и будем работать с начальными точками всех векторов как с точками регистрации стадии, так же, как они обычно используются в математике. Вектор будет определен так же, как общая точка, но у него будут свойства величины и угла. Взгляните на некоторые примеры векторов, определенных на стадии:
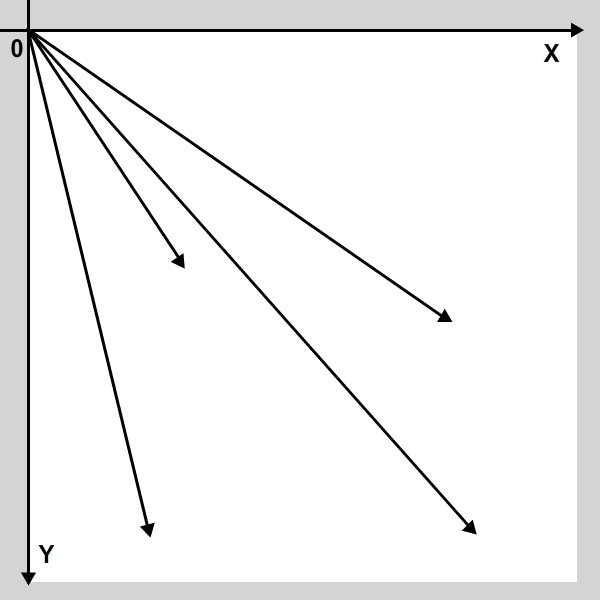
Как видите, вектор представлен стрелкой, и каждый вектор имеет определенную длину (или величину ) и указывает на определенный угол . Хвост каждого вектора находится в точке регистрации (0, 0) .
Для этого урока мы создадим простой класс EuclideanVector, используя класс Point для хранения координат вектора. Давайте создадим базовый векторный класс сейчас:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
|
package
{
import flash.geom.Point;
public class EuclideanVector
{
public var position:Point;
public var magnitude:Number;
public var angle:Number;
public function EuclideanVector(endPoint:Point)
{
position = endPoint;
}
}
}
|
В этом уроке мы поговорим о смысле и направлении вектора. Обратите внимание, что направление просто определяет линию, которая «содержит» вектор. Смысл в том, что определяет направление вектора вдоль этой линии.
Шаг 3: инверсия вектора
В этом уроке мы будем использовать выражение «обратный вектор». Инверсия вектора — это другой вектор с той же величиной и направлением, но противоположный смысл. Это переводит в вектор с противоположным сигналом координат первого вектора. Таким образом, вектор с конечной точкой (x, y) будет иметь обратный вектор с конечной точкой (-x, -y).
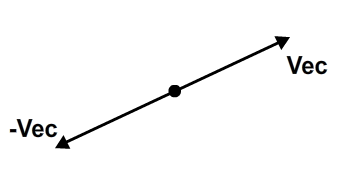
Давайте добавим функцию в наш класс EuclideanVector для возврата обратного вектора:
|
1
2
3
4
|
public function inverse():EuclideanVector
{
return new EuclideanVector(new Point(-position.x, -position.y));
}
|
Шаг 4: Добавление основных операций
Теперь, когда мы узнали, как определить вектор, давайте узнаем, как добавить два вектора: это так же просто, как добавить их координаты отдельно. Посмотрите на это изображение:
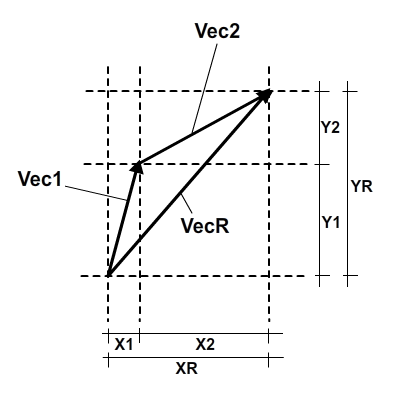
Если вы заметите на изображении, результатом сложения двух векторов будет другой вектор, и вы увидите, что его координаты являются суммой координат двух других векторов. В коде это будет выглядеть так:
|
1
2
3
4
5
6
7
|
public function sum(otherVector:EuclideanVector):EuclideanVector
{
position.x += otherVector.position.x;
position.y += otherVector.position.y;
return this;
}
|
Таким образом, мы можем сказать, что:
|
1
|
vecR == vec1.sum(vec2);
|
Шаг 5: Основные операции вычитания
Вычитание работает почти так же, как сложение, но вместо этого мы будем добавлять инверсию второго вектора к первому вектору.
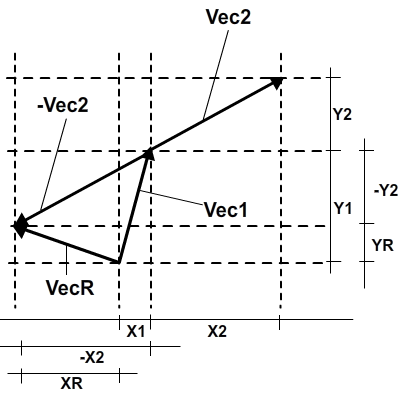
Уже известно, как суммировать два вектора, поэтому вот код для вычитания:
|
1
2
3
4
5
6
7
|
public function subtract(otherVector:EuclideanVector):EuclideanVector
{
position.x -= otherVector.position.x;
position.y -= otherVector.position.y;
return this;
}
|
Этот код чрезвычайно полезен для получения вектора, который идет от точки вектора к точке другого. Посмотрите еще раз на изображение, и вы увидите, что это правда. Это будет много использоваться в последующих примерах.
Шаг 6: Умножение основных операций на число
Умножение между вектором и числом (обычные числа известны как «скаляры» в векторной математике) приводит к вектору, величина которого умножается на это число, но все же указывает в том же направлении; он «растягивается», если скаляр больше 1, и сжимается, если скаляр находится между 0 и 1. Смысл нового вектора будет таким же, как и у исходного вектора, если скаляр положительный, или наоборот, если отрицательный. В основном это число «масштабирует» вектор. Посмотрите на картинку:
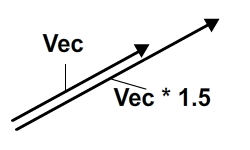
В коде мы только умножаем координаты вектора на число, которое затем масштабирует вектор:
|
1
2
3
4
5
6
7
|
public function multiply(number:Number):EuclideanVector
{
position.x *= number;
position.y *= number;
return this;
}
|
Шаг 7: Получение величины вектора
Чтобы получить величину вектора, мы будем использовать теорему Пифагора. Если вы забыли, что это, вот быстрое освежение в памяти:
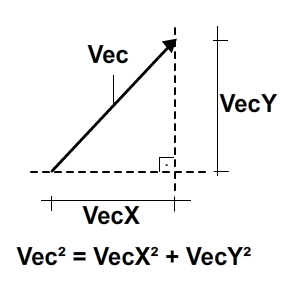
( Подробнее здесь .)
Код очень прост:
|
1
2
3
4
|
public function magnitude():Number
{
return Math.sqrt((position.x * position.x) + (position.y * position.y));
}
|
Вам также следует удалить строку public var magnitude:Number , так как это то, что мы будем использовать с этого момента.
Величина вектора всегда будет положительной, поскольку это квадратный корень из суммы двух положительных чисел.
Шаг 8: Получение угла вектора
Угол вектора — это угол между осью X и линией направления вектора. Угол измеряется от оси x и вращается против часовой стрелки до линии направления в декартовой системе:
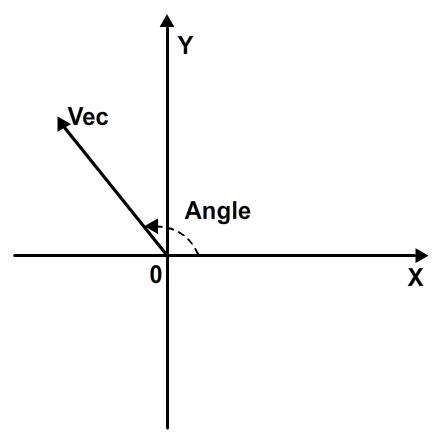
Однако в системе координат Flash, поскольку ось Y перевернута, этот угол будет измеряться вращением по часовой стрелке:
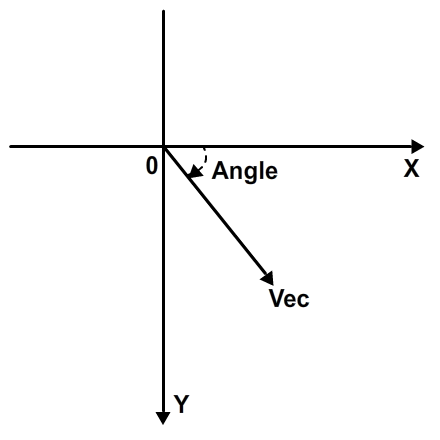
Это можно легко рассчитать, используя следующий код. Угол будет возвращен в радианах в диапазоне от 0 до 2pi. Если вы не знаете, что такое радианы или как их использовать, этот урок Майкла Джеймса Уильямса вам очень поможет.
|
01
02
03
04
05
06
07
08
09
10
11
|
public function angle():Number
{
var angle:Number = Math.atan2(position.y, position.x);
if (angle < 0)
{
angle += Math.PI * 2;
}
return angle;
}
|
Шаг 9: Точечный продукт
Точечное произведение между двумя векторами является числом, которое, по-видимому, не имеет смысла, но имеет два полезных применения. Давайте сначала посмотрим, как можно рассчитать скалярное произведение:
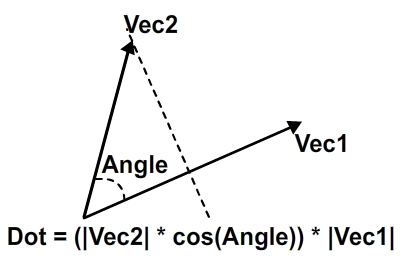
Но это также может быть получено координатами каждого вектора:
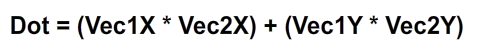
Точечный продукт может многое рассказать нам об угле между векторами: если он положительный, то угол колеблется от 0 до 90 градусов. Если он отрицательный, угол составляет от 90 до 180 градусов. Если это ноль, угол составляет 90 градусов. Это происходит потому, что в первой формуле только косинус отвечает за подачу точечного произведения «сигнала»: величины всегда положительны. Но мы знаем, что положительный косинус означает, что угол составляет от 0 до 90 градусов, и так далее для отрицательных косинусов и нуля.
Точечное произведение также может использоваться для представления длины вектора в направлении другого вектора. Думайте об этом как о проекции. Это оказывается чрезвычайно полезным в таких вещах, как теорема разделения осей (SAT) и ее реализация в AS3 для обнаружения столкновений и реагирования в играх.
Вот практический код для получения скалярного произведения между двумя векторами:
|
1
2
3
4
|
public function dot(otherVector:EuclideanVector):Number
{
return (position.x * otherVector.position.x) + (position.y * otherVector.position.y);
}
|
Шаг 10: наименьший угол между векторами
Угол между векторами, как видно на шаге 9, может быть задан скалярным произведением. Вот как это вычислить:
|
1
2
3
4
|
public function angleBetween(otherVector:EuclideanVector):Number
{
return Math.acos(dot(otherVector) / (magnitude() * otherVector.magnitude()));
}
|
Шаг 11: дальний угол между векторами
Существует также другой способ вычисления угла, который дает результаты между -pi и pi и всегда вычисляет угол, который идет от первого вектора ко второму вектору; это полезно, если вы хотите легко интегрировать с вращением экранного объекта (в диапазоне от -180 до 180).
Метод работает, получая угол для обоих векторов, затем вычитая углы и работая над результатом.
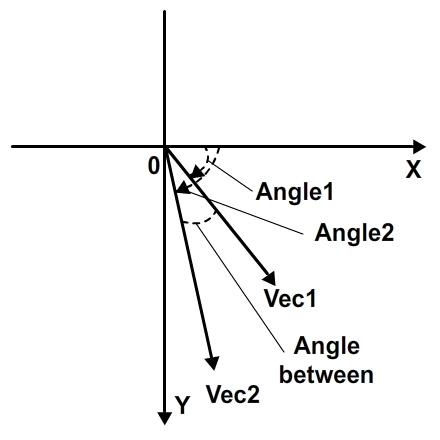
Код:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
|
public function rangedAngleBetween(otherVector:EuclideanVector):Number
{
var firstAngle:Number;
var secondAngle:Number;
var angle:Number;
firstAngle = Math.atan2(otherVector.position.y, otherVector.position.x);
secondAngle = Math.atan2(position.y, position.x);
angle = secondAngle — firstAngle;
while (angle > Math.PI)
angle -= Math.PI * 2;
while (angle < -Math.PI)
angle += Math.PI * 2;
return angle;
}
|
Обратите внимание, что этот угол возвращает положительное значение, если secondAngle выше, чем firstAngle , поэтому порядок, в котором вы получите дальний угол, повлияет на результат!
Шаг 12: нормализация вектора
Нормализация вектора означает, что его величина будет равна 1, сохраняя при этом направление и смысл вектора. Для этого мы умножаем вектор на 1/magnitude . Таким образом, его величина будет уменьшена или увеличена до 1.
|
1
2
3
4
5
6
7
8
|
public function normalize():EuclideanVector
{
var m:Number = magnitude();
position.x /= m;
position.y /= m;
return this;
}
|
Шаг 13: получение нормали вектора
Нормаль вектора — это другой вектор, который составляет 90 градусов к первому. Это можно рассчитать по следующим формулам:
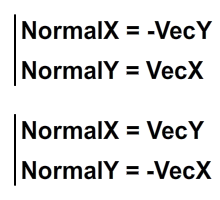
Формулы основаны на том факте, что, поскольку нормаль всегда перпендикулярна вектору, нам нужно только изменить порядок координат x и y и инвертировать одну из них, чтобы получить нормаль. На следующем изображении показан процесс:
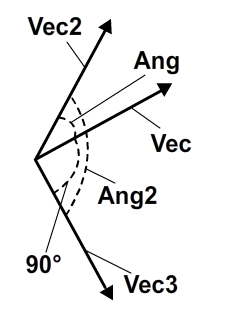
На изображении Vec является исходным вектором, Vec2 является вектором с замененными координатами Vec , а Vec3 является вектором с отрицательной y-координатой Vec2 . Ang и Ang2 являются переменными, но угол между Vec и Vec3 всегда составляет 90 градусов.
И код прост
|
1
2
3
4
5
6
7
8
9
|
public function normalRight():EuclideanVector
{
return new EuclideanVector(new Point(-position.y, position.x));
}
public function normalLeft():EuclideanVector
{
return new EuclideanVector(new Point(position.y, -position.x));
}
|
Шаг 14: вращение вектора
Чтобы повернуть вектор, мы предполагаем, что положение (0, 0) (его начальная точка) будет центром вращения. Вращаемая точка определяется по формуле:
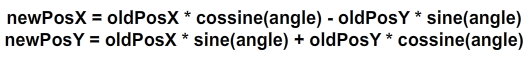
Эта формула получается путем применения матрицы вращения к этому вектору. Мы бы вышли за рамки этого урока, если бы углубились в матрицу и то, как она работает, поэтому я просто оставлю здесь формулу.
Код почти такой же:
|
01
02
03
04
05
06
07
08
09
10
|
public function rotate(angleInRadians:Number):EuclideanVector
{
var newPosX:Number = (position.x * Math.cos(angleInRadians)) — (position.y * Math.sin(angleInRadians));
var newPosY:Number = (position.x * Math.sin(angleInRadians)) + (position.y * Math.cos(angleInRadians));
position.x = newPosX;
position.y = newPosY;
return this;
}
|
Это конец наших основных векторных операций. Далее вы увидите, как использовать этот класс, чтобы делать интересные вещи. Вот наш класс на данный момент:
|
001
002
003
004
005
006
007
008
009
010
011
012
013
014
015
016
017
018
019
020
021
022
023
024
025
026
027
028
029
030
031
032
033
034
035
036
037
038
039
040
041
042
043
044
045
046
047
048
049
050
051
052
053
054
055
056
057
058
059
060
061
062
063
064
065
066
067
068
069
070
071
072
073
074
075
076
077
078
079
080
081
082
083
084
085
086
087
088
089
090
091
092
093
094
095
096
097
098
099
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
|
package
{
import flash.geom.Point;
public class EuclideanVector
{
public var position:Point;
public var angle:Number;
public function EuclideanVector(endPoint:Point)
{
position = endPoint;
}
public function inverse():EuclideanVector
{
return new EuclideanVector(new Point(-position.x, -position.y));
}
public function sum(otherVector:EuclideanVector):EuclideanVector
{
position.x += otherVector.position.x;
position.y += otherVector.position.y;
return this;
}
public function subtract(otherVector:EuclideanVector):EuclideanVector
{
position.x -= otherVector.position.x;
position.y -= otherVector.position.y;
return this;
}
public function multiply(number:Number):EuclideanVector
{
position.x *= number;
position.y *= number;
return this;
}
public function magnitude():Number
{
return Math.sqrt((position.x * position.x) + (position.y * position.y));
}
public function angle():Number
{
var angle:Number = Math.atan2(position.y, position.x);
if (angle < 0)
{
angle += Math.PI * 2;
}
return angle;
}
public function dot(otherVector:EuclideanVector):Number
{
return (position.x * otherVector.position.x) + (position.y * otherVector.position.y);
}
public function angleBetween(otherVector:EuclideanVector):Number
{
return Math.acos(dot(otherVector) / (magnitude() * otherVector.magnitude()));
}
public function rangedAngleBetween(otherVector:EuclideanVector):Number
{
var firstAngle:Number;
var secondAngle:Number;
var angle:Number;
firstAngle = Math.atan2(otherVector.position.y, otherVector.position.x);
secondAngle = Math.atan2(position.y, position.x);
angle = secondAngle — firstAngle;
while (angle > Math.PI)
angle -= Math.PI * 2;
while (angle < -Math.PI)
angle += Math.PI * 2;
return angle;
}
public function normalize():EuclideanVector
{
position.x /= magnitude();
position.y /= magnitude();
return this;
}
public function normalRight():EuclideanVector
{
return new EuclideanVector(new Point(-position.y, position.x));
}
public function normalLeft():EuclideanVector
{
return new EuclideanVector(new Point(position.y, -position.x));
}
public function rotate(angleInRadians:Number):EuclideanVector
{
var newPosX:Number = (position.x * Math.cos(angleInRadians)) — (position.y * Math.sin(angleInRadians));
var newPosY:Number = (position.x * Math.sin(angleInRadians)) + (position.y * Math.cos(angleInRadians));
position.x = newPosX;
position.y = newPosY;
return this;
}
}
}
|
Хорошо, мы рассмотрели создание векторного класса, теперь давайте попробуем его использовать.
Шаг 15: Определение того, находится ли точка внутри многоугольника
Действие начинается здесь. Определение того, находится ли точка внутри многоугольника или нет, является очень интересной темой, и существует множество способов ее достижения. В этой статье я представлю три метода, которые обычно используются:
- Алгоритм пересечения числа или четно-нечетного правила , который определяет, находится ли точка внутри многоугольника по числу ребер, которые «луч» отбрасывает из точки в бесконечность.
- Алгоритм числа обмоток , который дает ответ на основе суммы всех углов, образованных между последовательными вершинами многоугольника и проверяемой точкой.
- Алгоритм выпуклого многоугольника , который, как следует из названия, работает только для выпуклых многоугольников и основан на том, находится ли точка на определенной «стороне» каждого ребра многоугольника.
Все эти алгоритмы будут опираться на тот факт, что вы знаете координаты вершин (углов), которые определяют многоугольник.
Шаг 16. Алгоритм пересечения чисел или четно-нечетного правила.
Этот алгоритм может быть использован для любой формы. Это то, что вы читаете: любая форма, дырки или нет, выпуклые или нет. Он основан на том факте, что любой луч, отлитый из точки, которую вы хотите проверить на бесконечность, будет пересекать четное число ребер, если точка находится за пределами формы, или нечетное число ребер, если точка находится внутри фигуры. Это может быть доказано теоремой кривой Джордана , которая подразумевает, что вам придется пересечь границу между некоторым регионом и другим регионом, если вы хотите перейти от одного к другому. В нашем случае наши регионы находятся «внутри фигуры» и «вне фигуры».
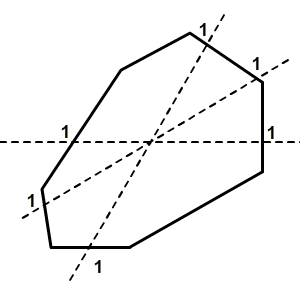
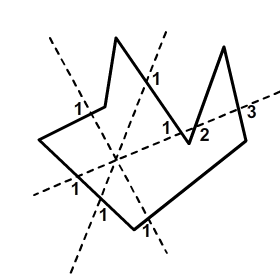
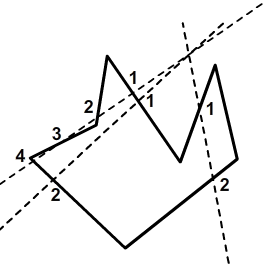
Код для этого алгоритма следующий:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
public function isPointInsideShape1(point:EuclideanVector, shapeVertices:Vector.<EuclideanVector>):Boolean
{
var numberOfSides:int = shapeVertices.length;
var i:int = 0;
var j:int = numberOfSides — 1;
var oddNodes:Boolean = false;
while (i < numberOfSides)
{
if ((shapeVertices[i].position.y < point.position.y && shapeVertices[j].position.y >= point.position.y) ||
(shapeVertices[j].position.y < point.position.y && shapeVertices[i].position.y >= point.position.y))
{
if (shapeVertices[i].position.x + (((point.position.y — shapeVertices[i].position.y) / (shapeVertices[j].position.y — shapeVertices[i].position.y)) *
(shapeVertices[j].position.x — shapeVertices[i].position.x)) < point.position.x)
{
oddNodes = !oddNodes;
}
}
j = i;
i++;
}
return oddNodes;
}
|
Он вернет false если точка не находится внутри фигуры, или true если точка находится внутри фигуры.
Шаг 17: Алгоритм числа обмоток
Алгоритм числа обмоток использует сумму всех углов, выполненных между проверяемой точкой и каждой парой точек, которые определяют многоугольник. Если сумма близка к 2pi, то проверяемая точка находится внутри вектора. Если оно близко к 0, то точка находится снаружи.
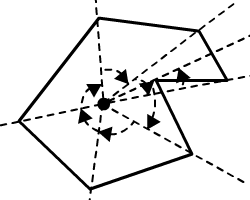
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
public function isPointInsideShape2(point:EuclideanVector, shapeVertices:Vector.<EuclideanVector>):Boolean
{
var numberOfSides:int = shapeVertices.length;
var i:int = 0;
var angle:Number = 0;
var rawAngle:Number = 0;
var firstVector:EuclideanVector;
var secondVector:EuclideanVector;
while(i < numberOfSides)
{
firstVector = new EuclideanVector(new Point(shapeVertices[i].position.x — point.position.x, shapeVertices[i].position.y — point.position.y));
secondVector = new EuclideanVector(new Point(shapeVertices[(i + 1) % numberOfSides].position.x — point.position.x, shapeVertices[(i + 1) % numberOfSides].position.y — point.position.y));
angle += secondVector.rangedAngleBetween(firstVector);
i++;
}
if(Math.abs(angle) < Math.PI)
return false;
else
return true;
}
|
Код использует ранжированный угол между векторами и дает место для неточностей: обратите внимание, как мы проверяем результаты суммирования всех углов. Мы не проверяем, равен ли угол в точности нулю или 2pi. Вместо этого мы проверяем, является ли оно меньше чем пи и больше ли пи, что является значительным медианным значением.
Шаг 18: алгоритм вогнутого многоугольника
Алгоритм вогнутого многоугольника основывается на том факте, что для вогнутого многоугольника точка внутри него всегда находится слева от ребер (если мы пересекаем их в направлении против часовой стрелки) или справа от ребер (если мы перебираем их по часовой стрелке).
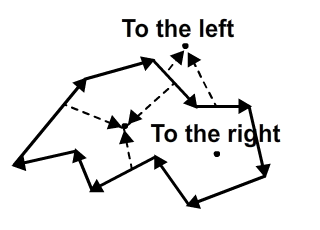
Представьте себе, что вы стоите в комнате, похожей на изображение выше, и идете по краям, левая рука тянется вдоль стены. В точке вдоль стены, где вы находитесь ближе всего к точке, которая вас интересует, если она справа от вас, то она должна находиться внутри комнаты; если он слева от вас, то он должен быть снаружи.
Проблема заключается в определении, находится ли точка слева или справа от ребра (которое в основном является вектором). Это делается с помощью следующей формулы:
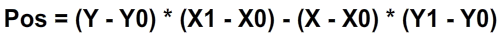
Эта формула возвращает число меньше 0 для точек справа от края и больше 0 для точек слева от него. Если число равно 0, точка лежит на краю и рассматривается внутри фигуры. Код следующий:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
|
public function isPointInsideShape3(point:EuclideanVector, shapeVertices:Vector.<EuclideanVector>):Boolean
{
var numberOfSides:int = shapeVertices.length;
var i:int = 0;
var firstEdgePoint:EuclideanVector;
var secondEdgePoint:EuclideanVector;
var leftOrRightSide:Boolean;
while(i < numberOfSides)
{
firstEdgePoint = shapeVertices[i];
secondEdgePoint = shapeVertices[(i + 1) % numberOfSides];
if(i == 0)
{
// Determining if the point is to the left or to the right of first edge
// true for left, false for right
leftOrRightSide = ((point.position.y — firstEdgePoint.position.y) * (secondEdgePoint.position.x — firstEdgePoint.position.x)) — ((point.position.x — firstEdgePoint.position.x) * (secondEdgePoint.position.y — firstEdgePoint.position.y)) > 0;
}
else
{
// Now all edges must be on the same side
if(leftOrRightSide && ((point.position.y — firstEdgePoint.position.y) * (secondEdgePoint.position.x — firstEdgePoint.position.x)) — ((point.position.x — firstEdgePoint.position.x) * (secondEdgePoint.position.y — firstEdgePoint.position.y)) < 0)
{
// Not all edges are on the same side!
return false;
}
else if(!leftOrRightSide && ((point.position.y — firstEdgePoint.position.y) * (secondEdgePoint.position.x — firstEdgePoint.position.x)) — ((point.position.x — firstEdgePoint.position.x) * (secondEdgePoint.position.y — firstEdgePoint.position.y)) > 0)
{
// Not all edges are on the same side!
return false;
}
}
i++;
}
// We looped through all vertices and didn’t detect different sides
return true;
}
|
Этот код работает независимо от того, определены ли у вас вершины фигуры по часовой стрелке или против часовой стрелки.
Шаг 19: Лучевое Приведение
Приведение лучей — это метод, часто используемый для обнаружения и визуализации столкновений. Он состоит из луча, который направлен из одной точки в другую (или в бесконечность). Этот луч состоит из точек или векторов и обычно останавливается при попадании на объект или край экрана. Как и в алгоритмах «точка в форме», существует множество способов создания лучей, и мы увидим два из них в этом посте:
- Алгоритм линии Брезенхэма, который является очень быстрым способом определения близких точек, которые дали бы приближение линии между ними.
- Метод DDA (Цифровой дифференциальный анализатор), который также используется для создания линии.
В следующих двух шагах мы рассмотрим оба метода. После этого мы увидим, как остановить луч при попадании на объект. Это очень полезно, когда вам нужно обнаружить столкновение с быстро движущимися объектами.
Шаг 20: Линейный алгоритм Брезенхэма
Этот алгоритм очень часто используется в компьютерной графике и зависит от соглашения о том, что линия всегда будет создаваться, указывая вправо и вниз. (Если необходимо создать строку в верхнем и левом направлениях, все будет инвертировано позже.) Давайте перейдем к коду:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
|
public function createLineBresenham(startVector:EuclideanVector, endVector:EuclideanVector):Vector.<EuclideanVector>
{
var points:Vector.<EuclideanVector> = new Vector.<EuclideanVector>();
var steep:Boolean = Math.abs(endVector.position.y — startVector.position.y) > Math.abs(endVector.position.x — startVector.position.x);
var swapped:Boolean = false;
if (steep)
{
startVector = new EuclideanVector(new Point(startVector.position.y, startVector.position.x));
endVector = new EuclideanVector(new Point(endVector.position.y, endVector.position.x));
}
// Making the line go downward
if (startVector.position.x > endVector.position.x)
{
var temporary:Number = startVector.position.x;
startVector.position.x = endVector.position.x;
endVector.position.x = temporary;
temporary = startVector.position.y;
startVector.position.y = endVector.position.y
endVector.position.y = temporary;
swapped = true;
}
var deltaX:Number = endVector.position.x — startVector.position.x;
var deltaY:Number = Math.abs(endVector.position.y — startVector.position.y);
var error:Number = deltaX / 2;
var currentY:Number = startVector.position.y;
var step:int;
if (startVector.position.y < endVector.position.y)
{
step = 1;
}
else
{
step = -1;
}
var iterator:int = startVector.position.x;
while (iterator < endVector.position.x)
{
if (steep)
{
points.push(new EuclideanVector(new Point(currentY, iterator)));
}
else
{
points.push(new EuclideanVector(new Point(iterator, currentY)));
}
error -= deltaY;
if (error < 0)
{
currentY += step;
error += deltaX;
}
iterator++;
}
if (swapped)
{
points.reverse();
}
return points;
}
|
Код создаст вектор евклидовых векторов AS3, который будет составлять линию. С помощью этого вектора мы можем позже проверить наличие коллизий.
Шаг 21: метод DDA
Реализация цифрового дифференциального анализатора используется для интерполяции переменных между двумя точками. В отличие от алгоритма линии Брезенхэма, этот метод для простоты создаст векторы только в целочисленных позициях. Вот код:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
public function createLineDDA(startVector:EuclideanVector, endVector:EuclideanVector):Vector.<EuclideanVector>
{
var points:Vector.<EuclideanVector> = new Vector.<EuclideanVector>();
var dx:Number;
var dy:Number;
var _x:Number = startPoint.position.x;
var _y:Number = startPoint.position.y;
var m:Number;
var i:int;
dx = endPoint.position.x — startPoint.position.x;
dy = endPoint.position.y — startPoint.position.y;
if (Math.abs(dx) >= Math.abs(dy))
m = Math.abs(dx);
else
m = Math.abs(dy);
points.push(new EuclideanVector(new Point(int(_x), int(_y))));
i = 1;
while (i <= m)
{
_x += dx / m;
_y += dy / m;
points.push(new EuclideanVector(new Point(int(_x), int(_y))));
i++;
}
return points;
}
|
Этот код также возвращает вектор евклидовых векторов AS3 .
Шаг 22: Проверка на столкновения с использованием лучей
Проверить столкновение с помощью лучей очень просто. Поскольку луч состоит из множества векторов, мы будем проверять наличие столкновений между каждым вектором и формой, пока один из них не будет обнаружен или пока не будет достигнут конец луча. В следующем коде shapeToCheck будет shapeToCheck , подобной той, которую мы использовали в шагах 13-16. Вот код:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
|
public function checkRayCollision(ray:Vector.<EuclideanVector>, shape:Vector.<EuclideanVector>):Boolean
{
var rayLength:int = ray.length;
var i:int = 0;
while(i < rayLength)
{
if(isPointInsideShape1(ray[i], shape))
{
return true;
}
i++;
}
return false;
}
|
Вы можете использовать любую функцию «точка-фигура», с которой вам удобно, но обратите внимание на ограничения последней!
Вывод
Вы готовы начать использовать эти знания везде сейчас! Это будет полезно много раз и сэкономит вам массу дополнительных вычислений при попытке сделать более сложные вещи во Flash.