До сих пор мы рассматривали структуры данных, которые организуют данные линейным образом. Связанные списки содержат данные от одного начального узла до одного конечного узла. Массивы хранят данные в смежных одномерных блоках.
обзор
В этом разделе мы увидим, как добавление еще одного измерения позволит нам представить новую структуру данных: дерево. В частности, мы будем рассматривать тип дерева, известного как двоичное дерево поиска. Деревья бинарного поиска принимают общую древовидную структуру и применяют набор простых правил, которые определяют структуру дерева.
Прежде чем мы узнаем об этих правилах, давайте узнаем, что такое дерево.
Обзор дерева
Дерево — это структура данных, в которой каждый узел имеет ноль или более дочерних элементов. Например, у нас могло бы быть дерево как это:
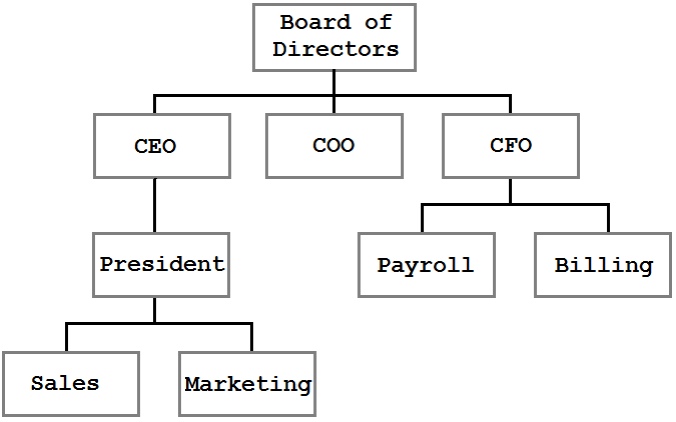
В этом дереве мы можем видеть организационную структуру бизнеса. Блоки представляют людей или подразделения внутри компании, а строки представляют отношения отчетности. Дерево — очень эффективный, логичный способ представления и хранения этой информации.
Дерево, показанное на предыдущем рисунке, является общим деревом. Он представляет отношения родитель / потомок, но для структуры нет правил. У генерального директора есть один прямой отчет, но с таким же успехом у него не может быть ни одного, ни двадцати. На рисунке слева от Маркетинга показаны Продажи, но этот порядок не имеет смысла. Фактически, единственным наблюдаемым ограничением является то, что каждый узел имеет не более одного родителя (а самый верхний узел, Совет директоров, не имеет родителя).
Обзор бинарного дерева поиска
Бинарное дерево поиска использует ту же базовую структуру, что и общее дерево, показанное на последнем рисунке, но с добавлением нескольких правил. Эти правила:
- Каждый узел может иметь ноль, одного или двух дочерних элементов.
- Любое значение, меньшее, чем значение узла, отправляется левому дочернему элементу (или дочернему элементу левого дочернего элемента).
- Любое значение, большее или равное значению узла, передается правому дочернему элементу (или его дочернему элементу).
Давайте посмотрим на дерево, построенное с использованием этих правил:
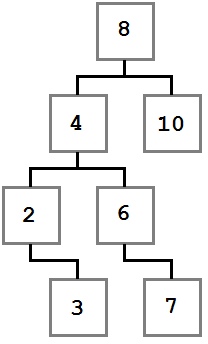
Обратите внимание, как указанные ограничения применяются на диаграмме. Каждое значение слева от корневого узла (восемь) имеет значение меньше восьми, а каждое значение справа больше или равно корневому узлу. Это правило применяется рекурсивно на каждом узле пути.
Имея это в виду, давайте подумаем о шагах по его созданию. Когда процесс начался, дерево было пустым, а затем было добавлено значение восемь. Поскольку это была первая добавленная стоимость, она была помещена в корневую (конечную родительскую) позицию.
Мы не знаем точный порядок добавления остальных узлов, но я приведу один из возможных путей. Значения будут добавлены с использованием метода с именем Add который принимает значение.
|
1
2
3
4
5
6
7
8
|
BinaryTree tree = new BinaryTree();
tree.Add(8);
tree.Add(4);
tree.Add(2);
tree.Add(3);
tree.Add(10);
tree.Add(6);
tree.Add(7);
|
Давайте пройдемся по первым нескольким пунктам.
Восемь был добавлен первым и стал рутом. Далее было добавлено четыре. Так как четыре меньше восьми, то нужно идти налево от восьми согласно правилу номер два. Поскольку у восьми нет ребенка слева, четверо становится непосредственным левым ребенком восьми лет.
Два добавляется дальше. два меньше восьми, поэтому он идет влево. Слева от восьми уже есть узел, поэтому логика сравнения выполняется снова. два меньше четырех, и четыре не имеют левого ребенка, поэтому два становятся левым ребенком четырех.
Три добавляются затем и идут слева от восьми и четырех. По сравнению с двумя узлами, он больше, поэтому три добавляются справа от двух согласно правилу номер три.
Этот цикл сравнения значений в каждом узле и последующей проверки каждого дочернего элемента до тех пор, пока не будет найден соответствующий слот, повторяется для каждого значения, пока не будет создана окончательная древовидная структура.
Класс узла
BinaryTreeNode представляет один узел в дереве. Он содержит ссылки на левый и правый дочерние IComparable.CompareTo если их нет), значение узла и метод IComparable.CompareTo который позволяет сравнивать значения узла, чтобы определить, должно ли значение идти слева или справа от текущего узла. Это весь класс BinaryTreeNode — как видите, он очень прост.
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class BinaryTreeNode : IComparable
where TNode : IComparable
{
public BinaryTreeNode(TNode value)
{
Value = value;
}
public BinaryTreeNode Left { get;
public BinaryTreeNode Right { get;
public TNode Value { get;
///
/// Compares the current node to the provided value.
///
/// The node value to compare to
/// 1 if the instance value is greater than
/// the provided value, -1 if less, or 0 if equal.
public int CompareTo(TNode other)
{
return Value.CompareTo(other);
}
}
|
Класс дерева двоичного поиска
Класс BinaryTree предоставляет базовые методы, необходимые для управления деревом: Add , Remove , метод Contains для определения наличия элемента в дереве, несколько методов обхода и перечисления (это методы, которые позволяют нам перечислять узлы в дереве в различных четко определенных порядках) и обычные методы Count и Clear .
Для инициализации дерева существует ссылка BinaryTreeNode которая представляет головной (корневой) узел дерева, и есть целое число, которое отслеживает, сколько элементов в дереве.
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
|
public class BinaryTree : IEnumerable
where T : IComparable
{
private BinaryTreeNode _head;
private int _count;
public void Add(T value)
{
throw new NotImplementedException();
}
public bool Contains(T value)
{
throw new NotImplementedException();
}
public bool Remove(T value)
{
throw new NotImplementedException();
}
public void PreOrderTraversal(Action action)
{
throw new NotImplementedException();
}
public void PostOrderTraversal(Action action)
{
throw new NotImplementedException();
}
public void InOrderTraversal(Action action)
{
throw new NotImplementedException();
}
public IEnumerator GetEnumerator()
{
throw new NotImplementedException();
}
System.Collections.IEnumerator System.Collections.IEnumerable.GetEnumerator()
{
throw new NotImplementedException();
}
public void Clear()
{
throw new NotImplementedException();
}
public int Count
{
get;
}
}
|
добавлять
| Поведение | Добавляет указанное значение в правильное местоположение в дереве. |
| Производительность | O (log n) в среднем; O (n) в худшем случае. |
Добавление узла в дерево не очень сложно и становится еще проще, когда задача упрощается до рекурсивного алгоритма. Есть два случая, которые необходимо рассмотреть:
- Дерево пусто.
- Дерево не пустое.
В первом случае мы просто выделяем новый узел и добавляем его в дерево. Во втором случае мы сравниваем значение со значением узла. Если значение, которое мы пытаемся добавить, меньше, чем значение узла, алгоритм повторяется для левого дочернего узла. В противном случае это повторяется для правого дочернего узла.
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
public void Add(T value)
{
// Case 1: The tree is empty.
if (_head == null)
{
_head = new BinaryTreeNode(value);
}
// Case 2: The tree is not empty, so recursively
// find the right location to insert the node.
else
{
AddTo(_head, value);
}
_count++;
}
// Recursive add algorithm.
private void AddTo(BinaryTreeNode node, T value)
{
// Case 1: Value is less than the current node value
if (value.CompareTo(node.Value) < 0)
{
// If there is no left child, make this the new left,
if (node.Left == null)
{
node.Left = new BinaryTreeNode(value);
}
else
{
// else add it to the left node.
AddTo(node.Left, value);
}
}
// Case 2: Value is equal to or greater than the current value.
else
{
// If there is no right, add it to the right,
if (node.Right == null)
{
node.Right = new BinaryTreeNode(value);
}
else
{
// else add it to the right node.
AddTo(node.Right, value);
}
}
}
|
удалять
| Поведение | Удаляет первое найденное ядро с указанным значением. |
| Производительность | O (log n) в среднем; O (n) в худшем случае. |
Удаление значения из дерева — это концептуально простая операция, которая на практике становится на удивление сложной.
На высоком уровне операция проста:
- Найти узел для удаления
- Убери это.
Первый шаг прост, и, как мы увидим, выполняется с использованием того же механизма, который использует метод Contains. Однако после идентификации удаляемого узла операция может занять один из трех путей, продиктованных состоянием дерева вокруг удаляемого узла. Три состояния описаны в следующих трех случаях.
Случай первый: удаляемый узел не имеет правого потомка.
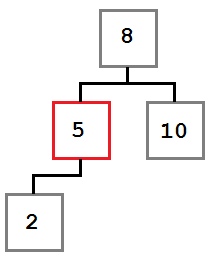
В этом случае операция удаления может просто переместить левого потомка, если он есть, на место удаленного узла. Результирующее дерево будет выглядеть так:
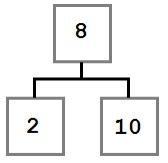
Случай второй: удаляемый узел имеет правого потомка, который, в свою очередь, не имеет левого потомка.
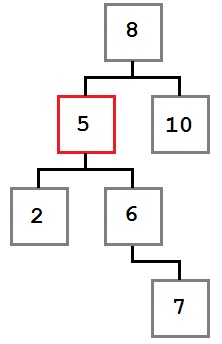
В этом случае мы хотим переместить правый дочерний элемент (шесть) удаленного узла на место удаленного узла. Результирующее дерево будет выглядеть так:
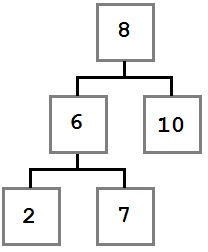
Случай третий: удаляемый узел имеет правого потомка, который, в свою очередь, имеет левого потомка.
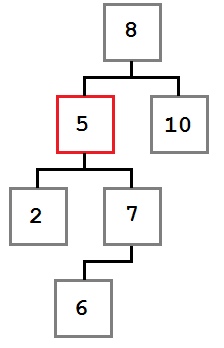
В этом случае самый левый дочерний элемент правого дочернего узла удаленного узла должен быть помещен в слот удаленного узла.
Давайте подумаем, почему это так. Есть два факта, которые мы знаем о поддереве, начинающемся с удаляемого узла (например, поддерево, корнем которого является узел со значением пять).
- Каждое значение справа от узла больше или равно пяти.
- Наименьшее значение в правом поддереве — самый левый узел.
Нам нужно поместить в слот удаленного узла значение, которое меньше или равно каждому узлу справа от него. Для этого нам нужно получить наименьшее значение с правой стороны. Поэтому нам нужен самый левый узел правого ребенка.
После удаления узла дерево будет выглядеть так:
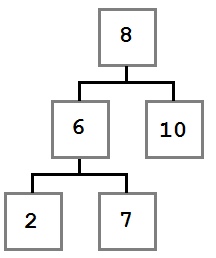
Теперь, когда мы понимаем три сценария удаления, давайте посмотрим на код, чтобы это произошло.
Стоит отметить: метод FindWithParent (см. Раздел «Содержит») возвращает FindWithParent узел, а также родительский FindWithParent узла. Это сделано потому, что когда узел удален, нам нужно обновить свойство Left или Right родительского Left чтобы оно указывало на новый узел.
Мы могли бы избежать этого, если бы все узлы сохраняли ссылку на своего родителя, но это привело бы к накладным расходам памяти на узел и расходам на ведение бухгалтерского учета, которые необходимы только в этом одном случае.
|
001
002
003
004
005
006
007
008
009
010
011
012
013
014
015
016
017
018
019
020
021
022
023
024
025
026
027
028
029
030
031
032
033
034
035
036
037
038
039
040
041
042
043
044
045
046
047
048
049
050
051
052
053
054
055
056
057
058
059
060
061
062
063
064
065
066
067
068
069
070
071
072
073
074
075
076
077
078
079
080
081
082
083
084
085
086
087
088
089
090
091
092
093
094
095
096
097
098
099
100
101
102
103
104
105
106
107
108
109
110
|
public bool Remove(T value)
{
BinaryTreeNode current, parent;
// Find the node to remove.
current = FindWithParent(value, out parent);
if (current == null)
{
return false;
}
_count—;
// Case 1: If current has no right child, current’s left replaces current.
if (current.Right == null)
{
if (parent == null)
{
_head = current.Left;
}
else
{
int result = parent.CompareTo(current.Value);
if (result > 0)
{
// If parent value is greater than current value,
// make the current left child a left child of parent.
parent.Left = current.Left;
}
else if (result < 0)
{
// If parent value is less than current value,
// make the current left child a right child of parent.
parent.Right = current.Left;
}
}
}
// Case 2: If current’s right child has no left child, current’s right child
// replaces current.
else if (current.Right.Left == null)
{
current.Right.Left = current.Left;
if (parent == null)
{
_head = current.Right;
}
else
{
int result = parent.CompareTo(current.Value);
if (result > 0)
{
// If parent value is greater than current value,
// make the current right child a left child of parent.
parent.Left = current.Right;
}
else if (result < 0)
{
// If parent value is less than current value,
// make the current right child a right child of parent.
parent.Right = current.Right;
}
}
}
// Case 3: If current’s right child has a left child, replace current with current’s
// right child’s left-most child.
else
{
// Find the right’s left-most child.
BinaryTreeNode leftmost = current.Right.Left;
BinaryTreeNode leftmostParent = current.Right;
while (leftmost.Left != null)
{
leftmostParent = leftmost;
leftmost = leftmost.Left;
}
// The parent’s left subtree becomes the leftmost’s right subtree.
leftmostParent.Left = leftmost.Right;
// Assign leftmost’s left and right to current’s left and right children.
leftmost.Left = current.Left;
leftmost.Right = current.Right;
if (parent == null)
{
_head = leftmost;
}
else
{
int result = parent.CompareTo(current.Value);
if (result > 0)
{
// If parent value is greater than current value,
// make leftmost the parent’s left child.
parent.Left = leftmost;
}
else if (result < 0)
{
// If parent value is less than current value,
// make leftmost the parent’s right child.
parent.Right = leftmost;
}
}
}
return true;
}
|
Содержит
| Поведение | Возвращает true, если дерево содержит предоставленное значение. В противном случае возвращается false. |
| Производительность | O (log n) в среднем; O (n) в худшем случае. |
Contains defers для FindWithParent , который выполняет простой алгоритм обхода FindWithParent , который выполняет следующие шаги, начиная с головного узла:
- Если текущий узел имеет значение null, вернуть значение null.
- Если текущее значение узла равно искомому значению, вернуть текущий узел.
- Если искомое значение меньше текущего значения, установите текущий узел на левый дочерний элемент и перейдите к шагу номер один.
- Установите текущий узел для правого потомка и перейдите к шагу номер один.
Поскольку Contains возвращает Boolean , возвращаемое значение определяется тем, возвращает ли FindWithParent ненулевое значение BinaryTreeNode (true) или нулевое (false).
Метод FindWithParent используется методом Remove. Выходной параметр parent не используется Contains .
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
public bool Contains(T value)
{
// Defer to the node search helper function.
BinaryTreeNode parent;
return FindWithParent(value, out parent) != null;
}
///
/// Finds and returns the first node containing the specified value.
/// is not found, it returns null.
/// which is used in Remove.
///
private BinaryTreeNode FindWithParent(T value, out BinaryTreeNode parent)
{
// Now, try to find data in the tree.
BinaryTreeNode current = _head;
parent = null;
// While we don’t have a match…
while (current != null)
{
int result = current.CompareTo(value);
if (result > 0)
{
// If the value is less than current, go left.
parent = current;
current = current.Left;
}
else if (result < 0)
{
// If the value is more than current, go right.
parent = current;
current = current.Right;
}
else
{
// We have a match!
break;
}
}
return current;
}
|
подсчитывать
| Поведение | Возвращает количество значений в дереве (0, если пусто). |
| Производительность | O (1) |
Поле счетчика увеличивается методом Add и уменьшается методом Remove .
|
1
2
3
4
5
6
7
|
public int Count
{
get
{
return _count;
}
}
|
ясно
| Поведение | Удаляет все узлы из дерева. |
| Производительность | O (1) |
|
1
2
3
4
5
|
public void Clear()
{
_head = null;
_count = 0;
}
|
обходов
Обход дерева — это алгоритмы, которые позволяют обрабатывать каждое значение в дереве в четко определенном порядке. Для каждого из рассмотренных алгоритмов в качестве примера ввода будет использовано следующее дерево.
Следующие примеры принимают параметр Action<T> . Этот параметр определяет действие, которое будет применено к каждому узлу при обработке обхода.
Раздел Order для каждого обхода будет указывать порядок, в котором будет проходить следующее дерево.
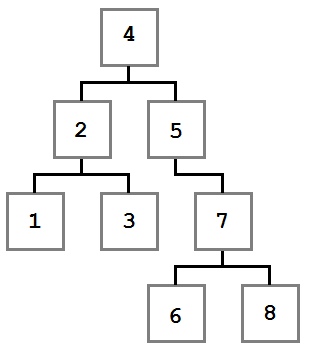
Предварительный заказ
| Поведение | Выполняет предоставленное действие для каждого значения в предзаказе (см. Описание ниже). |
| Производительность | На) |
| порядок | 4, 2, 1, 3, 5, 7, 6, 8 |
Обход предварительного заказа обрабатывает текущий узел, прежде чем перейти к левому, а затем к правому дочернему элементу. Начиная с корневого узла, четыре, действие выполняется со значением четыре. Затем обрабатывается левый узел и все его дочерние узлы, за ним следует правый узел и все его дочерние узлы.
Обычное использование обхода предварительного заказа должно было бы создать копию дерева, которое содержало бы не только те же самые значения узла, но также и ту же самую иерархию.
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
|
public void PreOrderTraversal(Action action)
{
PreOrderTraversal(action, _head);
}
private void PreOrderTraversal(Action action, BinaryTreeNode node)
{
if (node != null)
{
action(node.Value);
PreOrderTraversal(action, node.Left);
PreOrderTraversal(action, node.Right);
}
}
|
Postorder
| Поведение | Выполняет указанное действие для каждого значения в почтовом заказе (см. Описание ниже). |
| Производительность | На) |
| порядок | 1, 3, 2, 6, 8, 7, 5, 4 |
Обход после заказа рекурсивно посещает левого и правого дочернего узла, а затем выполняет действие с текущим узлом после завершения дочерних узлов.
Обходы по порядку следования часто используются для удаления всего дерева, например, в языках программирования, где каждый узел должен быть освобожден, или для удаления поддеревьев. Это происходит потому, что корневой узел обрабатывается (удаляется) последним, а его дочерние элементы обрабатываются таким образом, чтобы минимизировать объем работы, который должен выполнить алгоритм Remove .
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
|
public void PostOrderTraversal(Action action)
{
PostOrderTraversal(action, _head);
}
private void PostOrderTraversal(Action action, BinaryTreeNode node)
{
if (node != null)
{
PostOrderTraversal(action, node.Left);
PostOrderTraversal(action, node.Right);
action(node.Value);
}
}
|
Чтобы
| Поведение | Выполняет предоставленное действие для каждого значения в порядке (см. Описание ниже). |
| Производительность | На) |
| порядок | 1, 2, 3, 4, 5, 6, 7, 8 |
Обход по порядку обрабатывает узлы в порядке сортировки — в предыдущем примере узлы сортировались в числовом порядке от наименьшего к наибольшему. Это делается путем нахождения наименьшего (самого левого) узла и последующей его обработки перед обработкой более крупных (правых) узлов.
Обходы по порядку используются каждый раз, когда узлы должны обрабатываться в порядке сортировки.
В следующем примере показаны два разных метода выполнения обхода по порядку. Первый реализует рекурсивный подход, который выполняет обратный вызов для каждого пройденного узла. Второй удаляет рекурсию с помощью структуры данных стека и возвращает IEnumerator для прямого перечисления.
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
|
Public void InOrderTraversal(Action action)
{
InOrderTraversal(action, _head);
}
private void InOrderTraversal(Action action, BinaryTreeNode node)
{
if (node != null)
{
InOrderTraversal(action, node.Left);
action(node.Value);
InOrderTraversal(action, node.Right);
}
}
public IEnumerator InOrderTraversal()
{
// This is a non-recursive algorithm using a stack to demonstrate removing
// recursion.
if (_head != null)
{
// Store the nodes we’ve skipped in this stack (avoids recursion).
Stack> stack = new Stack>();
BinaryTreeNode current = _head;
// When removing recursion, we need to keep track of whether
// we should be going to the left node or the right nodes next.
bool goLeftNext = true;
// Start by pushing Head onto the stack.
stack.Push(current);
while (stack.Count > 0)
{
// If we’re heading left…
if (goLeftNext)
{
// Push everything but the left-most node to the stack.
// We’ll yield the left-most after this block.
while (current.Left != null)
{
stack.Push(current);
current = current.Left;
}
}
// Inorder is left->yield->right.
yield return current.Value;
// If we can go right, do so.
if (current.Right != null)
{
current = current.Right;
// Once we’ve gone right once, we need to start
// going left again.
goLeftNext = true;
}
else
{
// If we can’t go right, then we need to pop off the parent node
// so we can process it and then go to its right node.
current = stack.Pop();
goLeftNext = false;
}
}
}
}
|
GetEnumerator
| Поведение | Возвращает перечислитель, который перечисляет с использованием алгоритма обхода InOrder. |
| Производительность | O (1), чтобы вернуть перечислитель. Перечисление всех элементов является O (n). |
|
1
2
3
4
5
6
7
8
9
|
public IEnumerator GetEnumerator()
{
return InOrderTraversal();
}
System.Collections.IEnumerator System.Collections.IEnumerable.GetEnumerator()
{
return GetEnumerator();
}
|
Следующий
Это завершает пятую часть о бинарном дереве поиска. Далее мы узнаем о коллекции Set.