В этом разделе мы рассмотрим пять алгоритмов, используемых для сортировки данных в массиве. Мы начнем с наивного алгоритма пузырьковой сортировки и закончим самым распространенным алгоритмом сортировки общего назначения — быстрой сортировкой.
С каждым алгоритмом я объясню, как выполняется сортировка, а также предоставлю информацию о наилучшем, среднем и наихудшем уровне сложности как для производительности, так и для использования памяти.
Обмен
Чтобы немного облегчить чтение кода алгоритма сортировки, любой алгоритм сортировки, которому необходимо поменять значения в массиве по индексу, будет использовать общий метод Swap .
|
1
2
3
4
5
6
7
8
9
|
void Swap(T[] items, int left, int right)
{
if (left != right)
{
T temp = items[left];
items[left] = items[right];
items[right] = temp;
}
}
|
Пузырьковая сортировка
| Поведение | Сортирует входной массив, используя алгоритм пузырьковой сортировки. | ||
| сложность | Лучший случай | Средний случай | Худший случай |
| Время | На) | O (n 2 ) | O (n 2 ) |
| Космос | O (1) | O (1) | O (1) |
Bubble sort — это наивный алгоритм сортировки, который выполняет несколько проходов по массиву, каждый раз перемещая наибольшее несортированное значение вправо (конец) массива.
Рассмотрим следующий несортированный массив целых чисел:

При первом прохождении массива сравниваются значения три и семь. Поскольку семь больше трех, обмен не выполняется. Далее сравниваются семь и четыре. Семь больше четырех, поэтому значения меняются местами, перемещая семерку на один шаг ближе к концу массива. Массив теперь выглядит так:

Этот процесс повторяется, и в конечном итоге семерка заканчивается сравнением с восьмеркой, которая больше, поэтому обмен не может быть выполнен, и передача заканчивается в конце массива. В конце первого прохода массив выглядит так:

Поскольку был выполнен хотя бы один обмен, будет выполнен другой проход. После второго прохода шестерка перешла на позицию.

Опять же, поскольку был выполнен хотя бы один обмен, выполняется другой проход.
Следующий проход, однако, обнаруживает, что обмены не были необходимы, поскольку все элементы находятся в порядке сортировки. Поскольку обмены не выполнялись, известно, что массив отсортирован и алгоритм сортировки завершен.
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
|
public void Sort(T[] items)
{
bool swapped;
do
{
swapped = false;
for (int i = 1; i < items.Length; i++)
{
if (items[i — 1].CompareTo(items[i]) > 0)
{
Swap(items, i — 1, i);
swapped = true;
}
}
} while (swapped != false);
}
|
Сортировка вставок
| Поведение | Сортирует входной массив, используя алгоритм сортировки вставкой. | ||
| сложность | Лучший случай | Средний случай | Худший случай |
| Время | На) | O (n 2 ) | O (n 2 ) |
| Космос | O (1) | O (1) | O (1) |
Сортировка вставок работает, делая один проход через массив и вставляя текущее значение в уже отсортированную (начальную) часть массива. После обработки каждого индекса известно, что все, что встречалось до сих пор, сортируется, а все, что следует, неизвестно.
Чего ждать?
Важной концепцией является то, что сортировка вставок работает путем сортировки элементов по мере их появления. Поскольку он обрабатывает массив слева направо, мы знаем, что все слева от текущего индекса отсортировано. На этом рисунке показано, как массив сортируется при обнаружении каждого индекса:
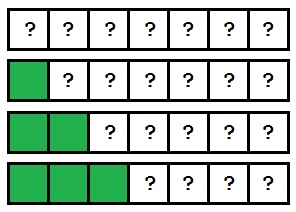
Поскольку обработка продолжается, массив становится все более и более отсортированным, пока он не будет полностью отсортирован.
Давайте посмотрим на конкретный пример. Ниже приведен несортированный массив, который будет отсортирован с использованием сортировки вставкой.

Когда начинается процесс сортировки, алгоритм сортировки начинается с нулевого индекса со значением три. Поскольку нет никаких значений, которые предшествуют этому, известно, что массив с индексом ноль включительно сортируется.
Затем алгоритм переходит к значению семь. Поскольку число семь больше, чем все в известном отсортированном диапазоне (который в настоящее время включает только три), известно, что значения вплоть до семи включительно находятся в порядке сортировки.
На данный момент известно, что индексы массива 0-1 сортируются, а 2-n находятся в неизвестном состоянии.
Значение по индексу два (четыре) проверяется следующим. Поскольку четыре меньше семи, известно, что четыре должны быть перемещены на свое место в области отсортированного массива. Теперь вопрос в том, к какому индексу в отсортированном массиве следует вставить значение. Метод для этого — FindInsertionIndex показанный в примере кода. Этот метод сравнивает значение для вставки (четыре) со значениями в отсортированном диапазоне, начиная с нулевого индекса, до тех пор, пока не найдет точку, в которую следует вставить значение.
Этот метод определяет, что индекс один (от трех до семи) является подходящей точкой вставки. Алгоритм вставки (метод Insert ) затем выполняет вставку, удаляя значение, которое будет вставлено из массива, и сдвигая все значения от точки вставки к удаленному элементу вправо. Массив теперь выглядит так:
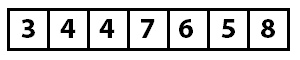
Теперь известно, что массив от индекса с нуля до двух сортируется, а все, начиная с индекса три до конца, неизвестно. Теперь процесс начинается снова с индекса три, который имеет значение четыре. Поскольку алгоритм продолжается, следующие вставки происходят, пока массив не отсортирован.
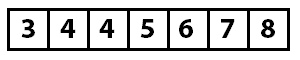
Когда нет дальнейших вставок, которые должны быть выполнены, или когда отсортированная часть массива является полным массивом, алгоритм завершается.
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
|
public void Sort(T[] items)
{
int sortedRangeEndIndex = 1;
while (sortedRangeEndIndex < items.Length)
{
if (items[sortedRangeEndIndex].CompareTo(items[sortedRangeEndIndex — 1]) < 0)
{
int insertIndex = FindInsertionIndex(items, items[sortedRangeEndIndex]);
Insert(items, insertIndex, sortedRangeEndIndex);
}
sortedRangeEndIndex++;
}
}
private int FindInsertionIndex(T[] items, T valueToInsert)
{
for (int index = 0; index < items.Length; index++)
{
if (items[index].CompareTo(valueToInsert) > 0)
{
return index;
}
}
throw new InvalidOperationException(«The insertion index was not found»);
}
private void Insert(T[] itemArray, int indexInsertingAt, int indexInsertingFrom)
{
// itemArray = 0 1 2 4 5 6 3 7
// insertingAt = 3
// insertingFrom = 6
// actions
// 1: Store index at in temp temp = 4
// 2: Set index at to index from -> 0 1 2 3 5 6 3 7 temp = 4
// 3: Walking backward from index from to index at + 1.
// Shift values from left to right once.
// 0 1 2 3 5 6 6 7 temp = 4
// 0 1 2 3 5 5 6 7 temp = 4
// 4: Write temp value to index at + 1.
// 0 1 2 3 4 5 6 7 temp = 4
// Step 1.
T temp = itemArray[indexInsertingAt];
// Step 2.
itemArray[indexInsertingAt] = itemArray[indexInsertingFrom];
// Step 3.
for (int current = indexInsertingFrom; current > indexInsertingAt; current—)
{
itemArray[current] = itemArray[current — 1];
}
// Step 4.
itemArray[indexInsertingAt + 1] = temp;
}
|
Выбор сортировки
| Поведение | Сортирует входной массив с использованием алгоритма сортировки выбора. | ||
| сложность | Лучший случай | Средний случай | Худший случай |
| Время | На) | O (n 2 ) | O (n 2 ) |
| Космос | O (1) | O (1) | O (1) |
Сортировка выбора — это своего рода гибрид между сортировкой пузырьков и сортировкой вставок. Подобно пузырьковой сортировке, он обрабатывает массив, перебирая от начала до конца снова и снова, выбирая одно значение и перемещая его в нужное место. Однако, в отличие от сортировки по пузырькам, она выбирает наименьшее несортированное значение, а не наибольшее. Как и сортировка вставкой, отсортированная часть массива является началом массива, тогда как при пузырьковой сортировке отсортированная часть находится в конце.
Давайте посмотрим, как это работает, используя тот же несортированный массив, который мы использовали.

На первом проходе алгоритм попытается найти наименьшее значение в массиве и поместить его в первый индекс. Это выполняется FindIndexOfSmallestFromIndex , который находит индекс наименьшего несортированного значения, начиная с предоставленного индекса.
С таким маленьким массивом мы можем сказать, что первое значение, три, является наименьшим значением, поэтому оно уже находится в правильном месте. На данный момент мы знаем, что значение в нулевом индексе массива является наименьшим значением и, следовательно, находится в правильном порядке сортировки. Итак, теперь мы можем начать проходить два — на этот раз, только просматривая записи массива от одного до n-1.
Второй проход определит, что четыре — это наименьшее значение в несортированном диапазоне, и поменяет значение во втором слоте на значение в слоте, в котором удерживались четыре (поменяйте местами четыре и семь). После завершения второго прохода значение четыре будет вставлено в отсортированную позицию.

Сортированный диапазон теперь от индекса ноль до индекса один, а несортированный диапазон — от индекса два до n-1. Когда каждый последующий проход заканчивается, отсортированная часть массива увеличивается, а несортированная часть становится меньше. Если в какой-либо момент пути вставки не выполняются, массив, как известно, сортируется. В противном случае процесс продолжается до тех пор, пока весь массив не будет отсортирован.
После еще двух проходов массив сортируется:

|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
public void Sort(T[] items)
{
int sortedRangeEnd = 0;
while (sortedRangeEnd < items.Length)
{
int nextIndex = FindIndexOfSmallestFromIndex(items, sortedRangeEnd);
Swap(items, sortedRangeEnd, nextIndex);
sortedRangeEnd++;
}
}
private int FindIndexOfSmallestFromIndex(T[] items, int sortedRangeEnd)
{
T currentSmallest = items[sortedRangeEnd];
int currentSmallestIndex = sortedRangeEnd;
for (int i = sortedRangeEnd + 1; i < items.Length; i++)
{
if (currentSmallest.CompareTo(items[i]) > 0)
{
currentSmallest = items[i];
currentSmallestIndex = i;
}
}
return currentSmallestIndex;
}
|
Сортировка слиянием
| Поведение | Сортирует входной массив, используя алгоритм сортировки слиянием. | ||
| сложность | Лучший случай | Средний случай | Худший случай |
| Время | O (n log n) | O (n log n) | O (n log n) |
| Космос | На) | На) | На) |
Разделяй и властвуй
До сих пор мы видели алгоритмы, которые работают путем линейной обработки массива. Эти алгоритмы имеют преимущество при работе с очень небольшим объемом памяти, но за счет квадратичной сложности времени выполнения. С сортировкой слиянием мы увидим наш первый алгоритм «разделяй и властвуй».
Алгоритмы «разделяй и властвуй» работают, разбивая большие проблемы на более мелкие, более легко решаемые. Мы видим эти типы алгоритмов в повседневной жизни. Например, мы используем алгоритм «разделяй и властвуй» при поиске в телефонной книге.
Если вы хотите найти имя Эрин Джонсон в телефонной книге, вы не начинаете с буквы А и переворачиваете страницу за страницей. Скорее всего, вы бы открыли телефонную книгу посередине. Если бы вы открыли М, вы бы перевернули несколько страниц, может быть, слишком далеко — возможно, Н. Тогда вы бы перевернулись вперед. И вы продолжали бы переворачивать взад и вперед все меньшие приращения, пока в конце концов не найдете нужную страницу (или оказались настолько близки, что пролистывание вперед имело смысл).
Насколько эффективны алгоритмы «разделяй и властвуй»?
Скажем, телефонная книга имеет длину 1000 страниц. Когда вы открываете середину, вы разбили проблему на две проблемы по 500 страниц. Предполагая, что вы находитесь не на нужной странице, теперь вы можете выбрать подходящую сторону для поиска и снова сократить проблему пополам. Теперь ваше проблемное пространство составляет 250 страниц. Поскольку проблема сокращается пополам все дальше и дальше, мы видим, что телефонную книгу на 1000 страниц можно искать всего за десять страниц. Это 1% от общего числа перелистываний страниц, которые могут понадобиться при выполнении линейного поиска.
Сортировка слиянием
Сортировка слиянием выполняется путем разрезания массива пополам снова и снова до тех пор, пока каждый элемент не станет длинным. Затем эти элементы объединяются (объединяются) в порядке сортировки.
Давайте начнем со следующего массива:
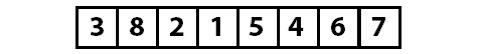
И теперь мы разрезаем массив пополам:

Теперь оба этих массива многократно разрезаются пополам, пока каждый элемент не станет самостоятельным:

Теперь, когда массив разделен на наименьшие возможные части, происходит процесс объединения этих частей в порядке сортировки.

Отдельные элементы становятся отсортированными группами по два, эти группы по два сливаются в отсортированные группы по четыре, а затем все они, наконец, объединяются в окончательный отсортированный массив.
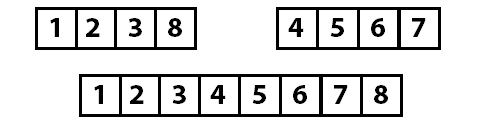
Давайте немного подумаем над отдельными операциями, которые нам нужно реализовать:
- Способ рекурсивного разбиения массивов. Метод
Sortделает это. - Способ объединения элементов в порядке сортировки. Метод
Mergeделает это.
Одним из соображений производительности сортировки слиянием является то, что в отличие от алгоритмов линейной сортировки сортировка слиянием будет выполнять всю логику разделения и объединения, включая любые выделения памяти, даже если массив уже находится в отсортированном порядке. Хотя производительность в худшем случае лучше, чем в алгоритмах линейной сортировки, производительность в худшем случае всегда будет хуже. Это означает, что это не идеальный кандидат при сортировке данных, о которых известно, что они почти отсортированы; например, при вставке данных в уже отсортированный массив.
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
|
public void Sort(T[] items)
{
if (items.Length <= 1)
{
return;
}
int leftSize = items.Length / 2;
int rightSize = items.Length — leftSize;
T[] left = new T[leftSize];
T[] right = new T[rightSize];
Array.Copy(items, 0, left, 0, leftSize);
Array.Copy(items, leftSize, right, 0, rightSize);
Sort(left);
Sort(right);
Merge(items, left, right);
}
private void Merge(T[] items, T[] left, T[] right)
{
int leftIndex = 0;
int rightIndex = 0;
int targetIndex = 0;
int remaining = left.Length + right.Length;
while(remaining > 0)
{
if (leftIndex >= left.Length)
{
items[targetIndex] = right[rightIndex++];
}
else if (rightIndex >= right.Length)
{
items[targetIndex] = left[leftIndex++];
}
else if (left[leftIndex].CompareTo(right[rightIndex]) < 0)
{
items[targetIndex] = left[leftIndex++];
}
else
{
items[targetIndex] = right[rightIndex++];
}
targetIndex++;
remaining—;
}
}
|
Быстрая сортировка
| Поведение | Сортирует входной массив с использованием алгоритма быстрой сортировки. | ||
| сложность | Лучший случай | Средний случай | Худший случай |
| Время | O (n log n) | O (n log n) | O (n 2 ) |
| Космос | O (1) | O (1) | O (1) |
Быстрая сортировка — это еще один алгоритм сортировки «разделяй и властвуй». Этот работает рекурсивно выполняя следующий алгоритм:
- Выберите сводный индекс и разделите массив на два массива. Это делается с помощью случайного числа в примере кода. Хотя есть и другие стратегии, я предпочел простой подход к этому образцу.
- Поместите все значения меньше, чем значение поворота, слева от точки поворота, а значения выше значения поворота вправо. Точка поворота теперь отсортирована — все справа больше; все слева меньше. Значение в точке поворота находится в правильном отсортированном месте.
- Повторяйте алгоритм поворота и разбиения для несортированных левого и правого разделов, пока каждый элемент не будет в известной отсортированной позиции
Давайте выполним быструю сортировку по следующему массиву:

Шаг первый говорит, что мы выбираем точку разделения, используя случайный индекс. В примере кода это делается в этой строке:
|
1
|
int pivotIndex = _pivotRng.Next(left, right);
|

Теперь, когда мы знаем индекс раздела (четыре), мы смотрим на значение в этой точке (шесть) и перемещаем значения в массиве так, чтобы все, что меньше значения, было слева от массива, а все остальное (значения больше). чем или равно) перемещается в правую часть массива. Имейте в виду, что перемещение значений может изменить индекс, в котором хранится значение раздела (мы скоро это увидим).
Обмен значений осуществляется методом разделения в примере кода.

На данный момент мы знаем, что шесть находится в правильном месте в массиве. Мы знаем это, потому что каждое значение слева меньше значения раздела, а все справа больше или равно значению раздела. Теперь мы повторим этот процесс на двух несортированных разделах массива.
Повторение выполняется в примере кода путем рекурсивного вызова метода быстрой сортировки для каждого из разделов массива. Обратите внимание, что на этот раз левый массив разделен по индексу один со значением пять. Процесс перемещения значений в соответствующие позиции перемещает значение пять в другой индекс. Я подчеркиваю это, чтобы подчеркнуть, что вы выбираете значение раздела, а не индекс раздела.
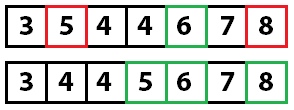
Быстрая сортировка снова:
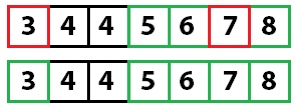
И быстрая сортировка в последний раз:
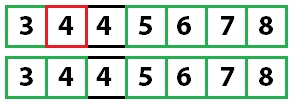
Осталось только одно несортированное значение, и поскольку мы знаем, что все остальные значения отсортированы, массив полностью отсортирован.
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
Random _pivotRng = new Random();
public void Sort(T[] items)
{
quicksort(items, 0, items.Length — 1);
}
private void quicksort(T[] items, int left, int right)
{
if (left < right)
{
int pivotIndex = _pivotRng.Next(left, right);
int newPivot = partition(items, left, right, pivotIndex);
quicksort(items, left, newPivot — 1);
quicksort(items, newPivot + 1, right);
}
}
private int partition(T[] items, int left, int right, int pivotIndex)
{
T pivotValue = items[pivotIndex];
Swap(items, pivotIndex, right);
int storeIndex = left;
for (int i = left; i < right; i++)
{
if (items[i].CompareTo(pivotValue) < 0)
{
Swap(items, i, storeIndex);
storeIndex += 1;
}
}
Swap(items, storeIndex, right);
return storeIndex;
}
|
В заключение
На этом мы завершаем заключительную часть Структуры данных: кратко: Часть 1. В этой серии из семи частей мы узнали о связанных списках, массивах, бинарном дереве поиска и коллекции наборов. Наконец, Роберт объяснил алгоритмы каждой обсуждаемой структуры данных.