В предыдущем посте Damn Cool Algorithms я говорил о BK-деревьях, умной структуре индексации, которая позволяет искать нечеткие совпадения в текстовой строке на основе расстояния Левенштейна — или любой другой метрике, которая подчиняется неравенству треугольника . Сегодня я собираюсь описать альтернативный подход, который позволяет выполнять нечеткий текстовый поиск по регулярному индексу: автоматы Левенштейна .
Вступление
Основная идея автоматов Левенштейна заключается в том, что можно построить конечный автомат который распознает точно набор строк в пределах заданного расстояния Левенштейна целевого слова. Затем мы можем ввести любое слово, и автомат примет или отклонит его в зависимости от того, является ли расстояние Левенштейна до целевого слова не больше расстояния, указанного при создании автомата. Кроме того, из-за природы FSA, он будет делать это за O (n) время с длиной тестируемой строки. Сравните это со стандартным алгоритмом динамического программирования Левенштейна, который занимает O (mn) времени, где m и n — длины двух входных слов! Таким образом, сразу становится очевидным, что автомат Левенштейна предоставляет нам, как минимум, более быстрый способ сопоставления многих слов с одним целевым словом и максимальным расстоянием — неплохое улучшение для начала!
Конечно, если бы это было единственным преимуществом автоматов Левенштейна, это была бы короткая статья. Это еще не все, но сначала давайте посмотрим, как выглядит автомат Левенштейна, и как мы можем его построить.
Строительство и оценка
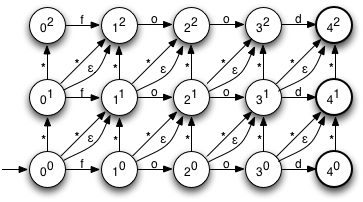
Диаграмма справа показывает NFA для автомата Левенштейна для слова «еда», с максимальным расстоянием редактирования 2. Как вы можете видеть, это очень регулярно, и конструкция довольно проста. Начальное состояние находится в левом нижнем углу. Состояния именуются с использованием нотации в стиле e , где n — количество использованных символов, а e — количество ошибок. Горизонтальные переходы представляют собой неизмененные символы, вертикальные переходы представляют вставки, а два типа диагональных переходов представляют замены (помеченные *) и удаления соответственно.
Давайте посмотрим, как мы можем построить NFA, такой как этот, учитывая входное слово и максимальное расстояние редактирования. Я не буду включать источник для класса NFA здесь, так как он довольно стандартный; подробности смотрите в Gist . Вот соответствующая функция в Python:
def levenshtein_automata(term, k):
nfa = NFA((0,0))
for i, c in enumerate(term):
for e in range(k +1):
# Correct character
nfa.add_transition((i, e), c,(i +1, e))
if e < k:
# Deletion
nfa.add_transition((i, e), NFA.ANY,(i, e +1))
# Insertion
nfa.add_transition((i, e), NFA.EPSILON,(i +1, e +1))
# Substitution
nfa.add_transition((i, e), NFA.ANY,(i +1, e +1))
for e in range(k +1):
if e < k:
nfa.add_transition((len(term), e), NFA.ANY,(len(term), e +1))
nfa.add_final_state((len(term), e))
return nfa
Это должно быть легко следовать; мы в основном строим переходы, которые вы видите на диаграмме, максимально простым способом, а также обозначаете правильный набор конечных состояний. Метки состояний — это кортежи, а не строки, причем кортежи используют те же обозначения, которые мы описали выше.
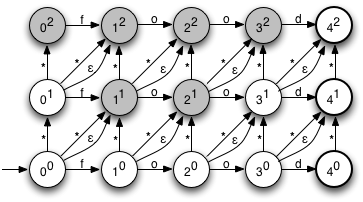
Поскольку это NFA, может быть несколько активных состояний. Между ними они представляют возможные интерпретации строки, обработанной до сих пор. Например, рассмотрим активные состояния после использования символов «f» и «x»:
Это указывает на то, что есть несколько возможных вариантов, которые соответствуют первым двум символам ‘f’ и ‘x’: одиночная замена, как в ‘fxod’, одиночная вставка, как в ‘fxood’, две вставки, как в ‘fxfood ‘, или замена и удаление, как в’ fxd ‘. Также включены несколько избыточных гипотез, таких как удаление и вставка, также приводящих к ‘fxod’. По мере обработки большего количества символов некоторые из этих возможностей будут исключены, а другие будут введены. Если после использования всех символов в слове принимающее (выделенное жирным шрифтом) состояние находится в наборе текущих состояний, есть способ преобразовать входное слово в целевое слово с двумя или менее изменениями, и мы знаем, что можем принять Слово как действительное.
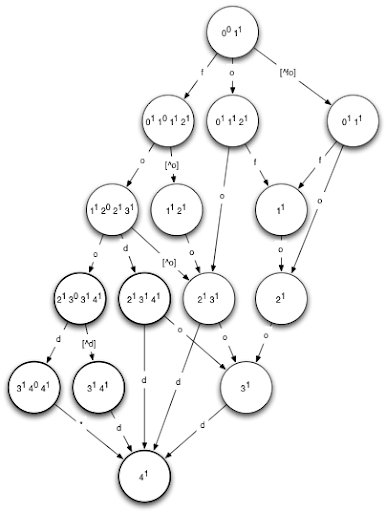
Фактическая оценка NFA напрямую имеет тенденцию быть довольно вычислительно дорогой из-за наличия нескольких активных состояний и эпсилон-переходов (то есть переходов, которые не требуют ввода символа), поэтому стандартная практика заключается в том, чтобы сначала преобразовать NFA в DFA с использованием конструкция powerset . Используя этот алгоритм, создается DFA, в котором каждое состояние соответствует набору активных состояний в исходном NFA. Мы не будем вдаваться в подробности о конструкции блока питания, так как это касается основной темы. Вот пример DFA, соответствующего NFA для входного слова «еда» с одной допустимой ошибкой:
Обратите внимание, что мы изобразили DFA для одной ошибки, так как DFA, соответствующий нашему NFA, выше, слишком сложен, чтобы удобно помещаться в блоге! Приведенный выше DFA будет принимать в точности те слова, у которых расстояние редактирования до слова «еда» равно 1 или меньше. Попробуйте: выберите любое слово и проследите его путь через DFA. Если вы в конечном итоге в полужирном состоянии, слово является действительным.
Я не буду здесь указывать источник для создания блока питания; это также в сущности для тех, кто заботится.
Вкратце возвращаясь к вопросу эффективности времени выполнения, вы можете задаться вопросом, насколько эффективна конструкция DFA Левенштейна. Мы можем построить NFA за время O (kn), где k — это расстояние редактирования, а n — длина целевого слова. Преобразование в DFA имеет наихудший случай времени O (2 n ) — что приводит к довольно экстремальному наихудшему случаю времени O (2 kn )! Но не все так страшно и мрачно по двум причинам: во-первых, автоматы Левенштейна не приблизятся к 2 n худшему случаю для построения DFA * . Во-вторых, некоторые очень умные компьютерные ученые придумали алгоритмы для создания DFA непосредственно за O (n) время, [ SCHULZ2002FAST] и даже метод, позволяющий полностью пропустить конструкцию DFA и использовать метод оценки на основе таблиц!
индексирование
Теперь, когда мы установили, что можно создавать автоматы Левенштейна, и продемонстрировали, как они работают, давайте посмотрим, как мы можем использовать их для эффективного поиска в индексе нечетких совпадений. Первое понимание и подход, который используется во многих работах [ SCHULZ2002FAST ] [ MIHOV2004FAST ], состоит в том, чтобы заметить, что словарь, то есть набор записей, которые вы хотите искать, сам может быть представлен как DFA. На самом деле, они часто хранятся как Trie или DAWGи то, и другое можно рассматривать как особые случаи ДФА. Учитывая, что и словарь, и критерии (автоматы Левенштейна) представлены в виде DFA, тогда можно эффективно пересечь два DFA, чтобы найти в словаре слова, точно соответствующие нашим критериям, используя очень простую процедуру, которая выглядит примерно так: :
def intersect(dfa1, dfa2):
stack =[("", dfa1.start_state, dfa2.start_state)]
while stack:
s, state1, state2 = stack.pop()
for edge inset(dfa1.edges(state1)).intersect(dfa2.edges(state2)):
state1 = dfa1.next(state1, edge)
state2 = dfa2.next(state2, edge)
if state1 and state2:
s = s + edge
stack.append((s, state1, state2))
if dfa1.is_final(state1)and dfa2.is_final(state2):
yield s
Таким образом, мы пересекаем оба DFA в одном шаге, следуя только ребрам, общим для обоих DFA, и отслеживая путь, по которому мы до сих пор шли. Каждый раз, когда оба DFA находятся в конечном состоянии, это слово находится в выходном наборе, поэтому мы выводим его.
Это очень хорошо, если ваш индекс хранится как DFA (или три или DAWG), но многих индексов нет: если они находятся в памяти, они, вероятно, находятся в отсортированном списке, и если они на диске, они, вероятно, в BTree или подобной структуре. Есть ли способ, которым мы можем изменить эту схему для работы с такими индексами, и при этом обеспечить ускорение на подходах грубой силы? Оказывается, что есть.
Критическое понимание здесь состоит в том, что с нашими критериями, выраженными как DFA, мы можем, учитывая входную строку, которая не соответствует, найти следующую строку (лексикографически говоря), которая делает, Интуитивно понятно, что это довольно легко сделать: мы сравниваем входную строку с DFA до тех пор, пока не сможем продолжить, например, потому что для следующего символа нет действительного перехода. Затем мы многократно следуем по краю с лексикографически наименьшей меткой, пока не достигнем конечного состояния. Здесь применимы два особых случая: во-первых, при первом переходе нам нужно следовать лексикографически наименьшей метке, превышающей символ, который не имел действительного перехода на предварительном шаге. Во-вторых, если мы достигнем состояния без действительного внешнего края, мы должны вернуться к предыдущему состоянию и повторить попытку. Это в значительной степени алгоритм «следования за стеной», применяемый к DFA.
В качестве примера рассмотрим приведенный выше DFA for food (1) и рассмотрим входное слово «foogle». Мы потребляем первые четыре символа в порядке, оставляя нас в состоянии 3 1 4 1 . Единственный выход отсюда — «d», а следующий символ — «l», поэтому мы возвращаемся на один шаг к предыдущему состоянию, 2 1 3 0 3 1 4 1 . Отсюда наш следующий символ — «g», и у «f» есть выход, поэтому мы берем этот край, оставляя нас в состоянии принятия (то же самое состояние, что и раньше, на самом деле, но с другим путем к it) с выходной строкой ‘fooh’ — следующая лексикографически следующая строка в DFA после ‘foogle’.
Вот код Python для него, как метод класса DFA. Как и ранее, я не включил шаблон для DFA, который все здесь .
def next_valid_string(self, input):
state =self.start_state
stack =[]
# Evaluate the DFA as far as possible
for i, x in enumerate(input):
stack.append((input[:i], state, x))
state =self.next_state(state, x)
ifnot state:break
else:
stack.append((input[:i+1], state,None))
ifself.is_final(state):
# Input word is already valid
return input
# Perform a 'wall following' search for the lexicographically smallest
# accepting state.
while stack:
path, state, x = stack.pop()
x =self.find_next_edge(state, x)
if x:
path += x
state =self.next_state(state, x)
ifself.is_final(state):
return path
stack.append((path, state,None))
return None
В первой части функции мы оцениваем DFA обычным образом, сохраняя стек посещенных состояний, а также путь и край, который мы собираемся попытаться выполнить из них. Затем, предполагая, что мы не нашли точного соответствия, мы выполняем поиск в обратном направлении, который мы описали выше, пытаясь найти наименьший набор переходов, которые мы можем выполнить, чтобы прийти в принимающее состояние. Для некоторых предостережений об общности этой функции читайте дальше …
Also needed is the utility function find_next_edge, which finds the lexicographically smallest outwards edge from a state that’s greater than some given input:
def find_next_edge(self, s, x):
if x isNone:
x = u'\0'
else:
x = unichr(ord(x)+1)
state_transitions =self.transitions.get(s,{})
if x in state_transitions or s inself.defaults:
return x
labels = sorted(state_transitions.keys())
pos = bisect.bisect_left(labels, x)
if pos < len(labels):
return labels[pos]
return None
With some preprocessing, this could be made substantially more efficient — for example, by pregenerating a mapping from each character to the first outgoing edge greater than it, rather than using binary search to find it in many cases. I once again leave such optimizations as an exercise for the reader.
Now that we have this procedure, we can finally describe how to search the index with it. The algorithm is surprisingly simple:
- Obtain the first element from your index — or alternately, a string you know to be less than any valid string in your index — and call it the ‘current’ string.
- Feed the current string into the ‘DFA successor’ algorithm we outlined above, obtaining the ‘next’ string.
- If the next string is equal to the current string, you have found a match — output it, fetch the next element from the index as the current string, and repeat from step 2.
- If the next string is not equal to the current string, search your index for the first string greater than or equal to the next string. Make this the new current string, and repeat from step 2.
And once again, here’s the implementation of this procedure in Python:
def find_all_matches(word, k, lookup_func):
"""Uses lookup_func to find all words within levenshtein distance k of word.
Args:
word: The word to look up
k: Maximum edit distance
lookup_func: A single argument function that returns the first word in the
database that is greater than or equal to the input argument.
Yields:
Every matching word within levenshtein distance k from the database.
"""
lev = levenshtein_automata(word, k).to_dfa()
match = lev.next_valid_string(u'\0')
while match:
next= lookup_func(match)
ifnotnext:
return
if match ==next:
yield match
next=next+ u'\0'
match = lev.next_valid_string(next)
One way of looking at this algorithm is to think of both the Levenshtein DFA and the index as sorted lists, and the procedure above to be similar to App Engine’s «zigzag merge join» strategy. We repeatedly look up a string on one side, and use that to jump to the appropriate place on the other side. If there’s no matching entry, we use the result of the lookup to jump ahead on the first side, and so forth. The result is that we skip over large numbers of non-matching index entries, as well as large numbers of non-matching Levenshtein strings, saving us the effort of exhaustively enumerating either of them. Hopefully it’s apparrent from the description that this procedure has the potential to avoid the need to evaluate either all of the index entries, or all of the candidate Levenshtein strings.
As a side note, it’s not true that for all DFAs it’s possible to find a lexicographically minimal successor to any string. For example, consider the successor to the string ‘a’ in the DFA that recognizes the pattern ‘a+b’. The answer is that there isn’t one: it would have to consist of an infinite number of ‘a’ characters followed by a single ‘b’ character! It’s possible to make a fairly simple modification to the procedure outlined above such that it returns a string that’s guaranteed to be a prefix of the next string recognized by the DFA, which is sufficient for our purposes. Since Levenshtein DFAs are always finite, though, and thus always have a finite length successor (except for the last string, naturally), we leave such an extension as an exercise for the reader. There are potentially interesting applications one could put this approach to, such as indexed regular expression search, which would require this modification.
Testing
First, let’s see this in action. We’ll define a simple Matcher class, which provides an implementation of the lookup_func required by our find_all_matches function:
classMatcher(object):
def __init__(self, l):
self.l = l
self.probes =0
def __call__(self, w):
self.probes +=1
pos = bisect.bisect_left(self.l, w)
if pos < len(self.l):
returnself.l[pos]
else:
returnNone
Note that the only reason we implemented a callable class here is because we want to extract some metrics — specifically, the number of probes made — from the procedure; normally a regular or nested function would be perfectly sufficient. Now, we need a sample dataset. Let’s load the web2 dictionary for that:
>>> words =[x.strip().lower().decode('utf-8')for x in open('/usr/share/dict/web2')]>>> words.sort()>>> len(words)234936
We could also use a couple of subsets for testing how things change with scale:
>>> words10 =[x for x in words if random.random()<=0.1]>>> words100 =[x for x in words if random.random()<=0.01]
And here it is in action:
>>> m =Matcher(words)>>> list(automata.find_all_matches('nice',1, m))[u'anice', u'bice', u'dice', u'fice', u'ice', u'mice', u'nace', u'nice', u'niche', u'nick', u'nide', u'niece', u'nife', u'nile', u'nine', u'niue', u'pice', u'rice', u'sice', u'tice', u'unice', u'vice', u'wice']>>> len(_)23>>> m.probes142
Working perfectly! Finding the 23 fuzzy matches for ‘nice’ in the dictionary of nearly 235,000 words required 142 probes. Note that if we assume an alphabet of 26 characters, there are 4+26*4+26*5=238 strings within levenshtein distance 1 of ‘nice’, so we’ve made a reasonable saving over exhaustively testing all of them. With larger alphabets, longer strings, or larger edit distances, this saving should be more pronounced. It may be instructive to see how the number of probes varies as a function of word length and dictionary size, by testing it with a variety of inputs:
| String length | Max strings | Small dict | Med dict | Full dict |
|---|---|---|---|---|
| 1 | 79 | 47 (59%) | 54 (68%) | 81 (100%) |
| 2 | 132 | 81 (61%) | 103 (78%) | 129 (97%) |
| 3 | 185 | 94 (50%) | 120 (64%) | 147 (79%) |
| 4 | 238 | 94 (39%) | 123 (51%) | 155 (65%) |
| 5 | 291 | 94 (32%) | 124 (43%) | 161 (55%) |
In this table, ‘max strings’ is the total number of strings within edit distance one of the input string, and the values for small, med, and full dict represent the number of probes required to search the three dictionaries (consisting of 1%, 10% and 100% of the web2 dictionary). All the following rows, at least until 10 characters, required a similar number of probes as row 5. The sample input string used consisted of prefixes of the word ‘abracadabra’.
Several observations are immediately apparrent:
- For very short strings and large dictionaries, the number of probes is not much lower — if at all — than the maximum number of valid strings, so there’s little saving.
- As the string gets longer, the number of probes required increases significantly slower than the number of potential results, so that at 10 characters, we need only probe 161 of 821 (about 20%) possible results. At commonly encountered word lengths (97% of words in the web2 dictionary are at least 5 characters long), the savings over naively checking every string variation are already significant.
- Although the size of the sample dictionaries differs by an order of magnitude, the number of probes required increases only a little each time. This provides encouraging evidence that this will scale well for very large indexes.
It’s also instructive to see how this varies for different edit distance thresholds. Here’s the same table, for a max edit distance of 2:
| String length | Max strings | Small dict | Med dict | Full dict |
|---|---|---|---|---|
| 1 | 2054 | 413 (20%) | 843 (41%) | 1531 (75%) |
| 2 | 10428 | 486 (5%) | 1226 (12%) | 2600 (25%) |
| 3 | 24420 | 644 (3%) | 1643 (7%) | 3229 (13%) |
| 4 | 44030 | 646 (1.5%) | 1676 (4%) | 3366 (8%) |
| 5 | 69258 | 648 (0.9%) | 1676 (2%) | 3377 (5%) |
This is also promising: with an edit distance of 2, although we’re having to do a lot more probes, it’s a much smaller percentage of the number of candidate strings. With a word length of 5 and an edit distance of 2, having to do 3377 probes is definitely far preferable to doing 69,258 (one for every matching string) or 234,936 (one for every word in the dictionary)!
As a quick comparison, a straightforward BK-tree implementation with the same dictionary requires examining 5858 nodes for a string length of 5 and an edit distance of 1 (with the same sample string used above), while the same query with an edit distance of 2 required 58,928 nodes to be examined! Admittedly, many of these nodes are likely to be on the same disk page, if structured properly, but there’s still a startling difference in the number of lookups.
One final note: The second paper we referenced in this article, [MIHOV2004FAST] describes a very nifty construction: a universal Levenshtein automata. This is a DFA that determines, in linear time, if any pair of words are within a given fixed Levenshtein distance of each other. Adapting the above scheme to this system is, also, left as an exercise for the reader.
The complete source code for this article can be found here.
* Robust proofs of this hypothesis are welcome.
[SCHULZ2002FAST] Fast string correction with Levenshtein automata
[MIHOV2004FAST] Fast approximate search in large dictionaries