Структурная непредвиденная ситуация (часть первая)

    public void clearViewCache(View view) {
	view.clearPositionCache();
	view.clearImageCache();
    }

Этот метод выражает более слабое требование синтаксического упорядочения, чем предыдущий, поскольку он не является составным методом, а определен в терминах двух вызовов метода, ни один из которых не предоставляет необходимый аргумент другому. Метод, порядок вызова которого не имеет необходимой явности, называется условным методом. В отличие от предыдущего метода, который не допускал переупорядочения, этот условный метод, очевидно, мог быть записан как:

    public void clearViewCache(View view) {
	view.clearImageCache();
	view.clearPositionCache();
    }

Это, конечно, не может иметь место. Не принимая аргументов и не возвращая значений, оба вызова метода теряют свои побочные эффекты, поэтому второй вызов может собирать информацию, измененную первым, так что изменение порядка вызовет ошибку. Независимо от того, является ли очевидное отсутствие необходимого порядка скрытным приказом, который необходимо соблюдать, или приглашением перемешать по своему желанию, не имеет значения; Суть в том, что сам метод не дает никаких синтаксических доказательств в любом случае и при этом предполагает упорядоченность, а в композиции нет. Это предположение может быть ошибочным, но, тем не менее, оно существует. Случайность поднимает вопросы, которых состав полностью избегает.

Программисты ценят намерения. Например, объяснение экстремального программирования Кента Бека утверждает, что сущность простого кода заключается в том, что он «раскрывает свои намерения». Роберт К. Мартин идет дальше, утверждая, что даже больше, чем простое программирование, «архитектура — это намерение». Увеличивающееся ограничение обычно коррелирует с возрастающим намерением, потому что с возрастающим ограничением появляется меньшее количество альтернатив и, следовательно, меньше возможностей для двусмысленности и неправильного толкования. Учитывая, что состав ограничивает порядок больше, чем случайность, составные методы показывают больше намерения, чем условные методы, и поэтому пользуются только этим узким измерением превосходством.

Некоторые обозначения могут помочь. Так же, как оператор o означает композицию, допустим, что оператор \ означает случайность. Таким образом, второй фрагмент может быть записан как:

clearViewCache = clearPositionCache \ clearImageCache

И это, по определению, равно:

clearViewCache = clearImageCache \ clearPositionCache

Как программист может использовать эту тривиальность для прояснения намерений? Один из способов — минимизировать количество условных методов и максимизировать количество составных методов. Здесь, увы, вселенная смеется над программистом из-за некоторых неудачных комбинаторных правил; свободно:

Композиция + композиция = композиция.
Случайность + случайность = случайность.
Состав + случайность = случайность.

То есть, fogoh представляет собой составной метод, но fo (g \ h) является условным методом, даже если он содержит оператор композиции. Однажды загубленная неопределенностью порядка, ни один метод не может избежать непредвиденных обстоятельств. Тем не менее, кажется, стыдно скрывать даже частичное намерение под замешательством. Поэтому, скажем далее, метод, сформированный исключительно вокруг оператора композиции или непредвиденного обстоятельства, например, последовательности вызова k \ m \ p \ s или последовательности komopos.— мы будем называть «простой по порядку» метод, в то время как один, обладающий как составными, так и операциями на случай непредвиденных обстоятельств, мы будем называть «сложным по порядку». Таким образом, максимизация намерения превращает составные методы порядка в простые шарды порядка.

Рассматривать:

a = f \ (го)

Если мы введем составной метод j такой, что j = goh, то вышеупомянутое порядковое соединение сводится к двум простым по порядку методам:

a = f \ j
j = goh

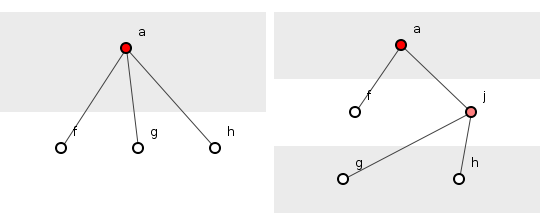
Как показано на рисунке 1, это сокращение происходит за счет как дополнительных методов, так и глубины, но в то время как непредвиденные обстоятельства исходного метода запутали его общий порядок вызовов, по крайней мере, один из новых методов явно подразумевает порядок, который он формулирует. Часть программы была спасена от непредвиденных обстоятельств, даже если общая непредвиденная ситуация остается.

Рисунок 1: Порядок составного сокращения непредвиденных расходов до (слева) и после (справа).

К сожалению, нет никакой гарантии, что метод сложного порядка может разложиться на множество простых для порядка методов. Вызов метода с несколькими аргументами по своей природе связан с непредвиденными обстоятельствами, поскольку методы не диктуют порядок оценки функциональных аргументов. (Действительно, оператор \ немного больше запятой, разделяющей аргументы функции.) Возникают два вопроса. При успешном сокращении является ли набор простых по порядку методов, на которые метод сложного порядка разлагается уникальным?

Свойства.

Некоторые свойства непредвиденных обстоятельств:

1. fo (g \ h) = f (g, h)
2. Коммутативность: f \ g = g \ f
3. Ассоциативность: (f \ g) \ h = f \ (g \ h)
4. Композиция распределяется справа над случайностью: (f \ g) oh = (foh) \ (goh)

Другие существуют, чтобы быть исследованным в более позднем посте.

Сложенный порядок — простой.

Давайте рассмотрим некоторый реальный производственный код. FitNesse предоставляет все следующие фрагменты, первый из класса PageDriver .

  private NodeList getMatchingTags(NodeFilter filter) throws Exception {
    String html = examiner.html();
    Parser parser = new Parser(new Lexer(new Page(html)));
    NodeList list = parser.parse(null);
    NodeList matches = list.extractAllNodesThatMatch(filter, true);
    return matches;
  }

Моделирование этого как его основного вызова метода приводит к уравнению:

getMatchingTags = extractAllNodesThatMatch o синтаксический анализ o новый анализатор o новый Lexer o новая страница o html

Это представляет собой совершенный, простой для порядка, составной метод, каждый вызов метода зависит от предыдущего. Выражая приказ, который не терпит взлома, программист помогает прояснить намерение метода, освобождая программиста от мысли о потенциальных альтернативах. Будучи простым для заказа , PageDriver не предлагает сложность заказа для уменьшения.

Условный приказ — простой.

  public void close() throws IOException {
    super.close();
    removeStopTestLink();
    publishAndAddLog();
    maybeMakeErrorNavigatorVisible();
    finishWritingOutput();
  }

Этот метод в классе TestHtmlFormatter представляет случайное простое условие , уравнение которого:

close = close \ removeStopTestLink \ publishAndAddLog \ MaybeMakeErrorNavigatorVisible \ finishWritingOutput

Опять же, будучи простым по порядку, TestHtmlFormatter стоит неприводимым, но, в отличие от предыдущего примера, это вряд ли хорошо говорит о дизайне метода. Намерение программиста не оставило следов в используемом синтаксисе, полностью растворившись в туманной семантике. Тем не менее, по крайней мере, метод является простым, а не составным порядком: концентрация непредвиденных обстоятельств в такой чистой неявности порядка, по крайней мере, выделяет цели для рефакторингов, раскрывающих намерения, на которые указывают сокращения составного порядка. Повторим, что сокращения составных порядков не уменьшают общую непредвиденную ситуацию системы как таковую — они реорганизуют исследуемый метод, но не реорганизуют вызываемый метод. Вместо этого сокращения действуют как нефтеперерабатывающие заводы, перекачивая шлам от непредвиденных обстоятельств в металлические бочки для последующей детоксикации.

Порядок-соединение.

Конструктор MultiUserAuthenticator представляет минималистский пример порядка компоновки :

  public MultiUserAuthenticator(String passwdFile) throws IOException {
    PasswordFile passwords = new PasswordFile(passwdFile);
    users = passwords.getPasswordMap();
    cipher = passwords.getCipher();
  }

Ясно, что метод составного заказа условный, это может быть смоделировано с помощью:

MultiUserAuthenticator = (getPasswordMap \ getCipher) o новый PasswordFile

Выполнение сокращения составного порядка включает в себя рефакторинг метода, чтобы минимизировать размер составных порядков, из которых он построен. Наиболее очевидное сокращение для выполнения вышеизложенного извлекает новый метод f = getPasswordMap \ getCipher , таким образом производя два уравнения:

MultiUserAuthenticator = fo новый PasswordFile
f = getPasswordMap \ getCipher

Это устраняет всю сложность порядка, приводя к составному методу и простому порядку условному методу, и, следовательно, завершает редукцию. Полученный исходный код будет выглядеть примерно так:

  public MultiUserAuthenticator(String passwdFile) throws IOException {
    PasswordFile passwords = new PasswordFile(passwdFile);
    f(passwords);
  }

  private f(PasswordFile passwords) throws IOException {
    users = passwords.getPasswordMap();
    cipher = passwords.getCipher();
  }

( Возможно, существует лучшее имя для метода f () .)

Опять же, это сокращение влечет за собой увеличение глубины. Другие сокращения представляют себя, однако. Учитывая приведенное выше правило (4), исходная модель конструктора могла бы быть записана как:

MultiUserAuthenticator = (getPasswordMap o новый PasswordFile) \ (getCipher o новый PasswordFile)

Это сводится к трем уравнениям простого порядка:

MultiUserAuthenticator = f \ g
f = getPasswordMap o новый PasswordFile
g = getCipher o новый PasswordFile

Однако такая формулировка страдает от многих недостатков, таких как двойной вызов конструктора PasswordFile ; если бы это был вычислительно дорогой фрагмент кода, то только производительность могла бы сделать эту вторую формулировку несостоятельной. Сокращение, тем не менее, отвечает на наш вопрос. Является ли множество простых по порядку методов, на которые метод сложного порядка разлагается, уникальным? Нет .

Проблема нормализации.

ProcessTestFile () метод PageHistory освещает некоторые интересные трудности:

  void processTestFile(TestResultRecord record) throws ParseException {
    Date date = record.getDate();
    addTestResult(record, date);
    countResult(record);
    setMinMaxDate(date);
    setMaxAssertions(record);
    pageFiles.put(date, record.getFile());
  }