Изучение структур данных и алгоритмов не имеет большого числа последователей в сообществе Ruby, потому что мы часто спрашиваем «в чем смысл?». На практике нам редко приходится реализовывать классические структуры, такие как стеки и очереди. Но, узнав о них, мы можем улучшить нашу способность рассуждать о коде. Что еще более важно, структуры данных очень интересны для изучения!
В этой статье мы рассмотрим структуру данных «куча» вместе с некоторыми из связанных алгоритмов. Я предполагаю, что у вас есть базовый дескриптор асимптотической нотации и Ruby.
мотивация
У всех нас слишком много писем. В примере, где нам удалось назначить каждому письму в нашей папке входящих сообщений приоритет или значение ключа (т. Е. Число), мы хотим иметь возможность делать следующие вещи:
- Получить письмо с самым большим ключом
- Удалите и получите письмо с самым большим ключом
Это будет связано с большим количеством электронных писем, поэтому мы хотим, чтобы эти операции были довольно быстрыми, асимптотически. Какую структуру данных мы должны использовать для достижения этих целей? Оказывается, что с помощью кучи мы выполняем операцию № 1 за \ (O (1) \) время и операцию № 2 за \ (O (\ log_2 {n}) \).
Концепции
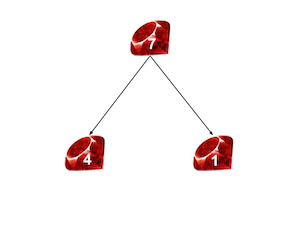
Более конкретно, мы будем иметь дело с «максимальной кучей». С этого момента мы будем использовать термины «максимальная куча» и «куча» взаимозаменяемо. Максимальная куча может быть визуализирована как частично завершенный двоичный файл, например:
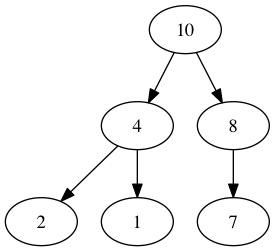
Особенностью этого является то, что для любого узла дочерние элементы этого узла имеют ключи, меньшие или равные ключам этого узла. Обратите внимание, что на рисунке выше ключи для каждого узла записаны внутри узла. Обычно кучи хранятся в виде массивов. Таким образом, наш пример выше будет выглядеть так:
[10, 4, 8, 2, 1, 7] Мы создаем массив, проходя сверху вниз и слева направо через двоичное представление дерева и добавляя ключи узла в массив. Важно знать, что не все массивы являются кучей. Например, возьмите:
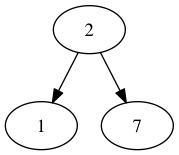
[2, 1, 7]
Мы можем представить это как:
что не куча, так как \ (7> 2 \). По сути, куча — это массив со специальным условием, которое при отображении в виде дерева сохраняет свойство max heap. Другими словами, дочерние элементы каждого узла имеют значения ключа меньше, чем у самого узла.
Построение кучи
Первая проблема, с которой мы сталкиваемся, это то, что наш список электронных писем может иметь произвольно упорядоченный массив приоритетов, которые могут не образовывать кучу. Как мы возьмем этот массив и упорядочим его так, чтобы он образовывал кучу?
Ну, это кажется довольно сложной проблемой, которую нужно решать сразу, поэтому давайте сначала разберемся с уменьшенной версией. Допустим, нам дали массив, который был всего лишь одним «обменом» от превращения в кучу. Итак, у нас есть некоторый узел v так что его левое и правое поддеревья являются кучами, но поддерево с корнем в v не является кучей:
Мы можем решить эту проблему рекурсивно. Во-первых, поменяйте 4 и 10. Затем мы снова столкнулись с почти одной и той же проблемой, просто в другом месте дерева после \ (9> 4 \) и \ (7> 4 \), так что мы можем решить ее используя тот же метод. Мы продолжаем делать это, пока \ (4 \) не «опустится» на дно дерева и не превратится в лист. Вот как будет работать наш подход:
fix_one_error(array, index): 1. If array[index] is a leaf node or is greater than both its children, return. 2. larger_index = the index of the larger child of the node at array[index] 3. Swap array[i] and array[larger_index] 4. fix_one_error(array, larger_index)
Хорошо, давайте реализуем идеи в Ruby. Прежде всего, нам нужна пара методов, чтобы дать нам индексы потомков данного узла в представлении массива:
class Heap attr_accessor :heap_size, :array_rep def left_child(index) 2*index + 1 end def right_child(index) 2*index + 2 end def left_child_key(index) @array_rep[left_child(index)] end def right_child_key(index) @array_rep[right_child(index)] end end
Во-вторых, нам нужен какой-то способ узнать, является ли данный элемент листовым узлом или нет:
class Heap ... def leaf_node?(index) return index >= @heap_size/2 end ... end
Наконец, мы должны иметь возможность определить, удовлетворяет ли узел уже свойству max heap (в этом случае нам не нужно продолжать исправлять ошибки):
class Heap ... def satisfied?(index) @array_rep[index] >= left_child_key(index) and @array_rep[index] >= right_child_key(index) end ... end
Детали того, как работают эти четыре метода, не являются невероятно важными, но выделение нескольких куч с помеченными индексами массива может сделать их внутреннюю механику довольно ясной. Теперь мы можем выписать наш алгоритм во всей его красе:
class Heap ... def fix_one_error(index) return if leaf_node?(index) || satisfied?(index) left_child_key = @array_rep[left_child(index)] right_child_key = @array_rep[right_child(index)] larger_child = if left_child_key > right_child_key then left_child(index) else right_child(index) end @array_rep[index], @array_rep[larger_child] = @array_rep[larger_child], @array_rep[index] fix_one_error(larger_child) end ... end
Обратите внимание, что мы очень внимательно следили за псевдокодом / описанием. Повторно меняйте местами до тех пор, пока либо узел не удовлетворит свойство max heap, либо он не сместится вниз по дереву, чтобы стать листовым узлом.
Сложность «исправить одну ошибку»
На первый взгляд, мы можем подумать, что наш алгоритм fix_one_error — это \ (O (n) \), но, решив рекуррентность, мы обнаружим, что это \ (O (\ log_2 {n}) \). Интуитивное объяснение довольно ясно: каждый обмен, полученный в результате вызова fix_one_error занимает \ (O (1) \) время, а когда у нас есть элементы \ (n \), наше дерево имеет уровни \ (\ log_2 {n} \) в таким образом, мы получаем \ (O (\ log_2 {n}) \) в качестве нашей временной сложности.
Завершение строительства
Но мы еще не решили всю проблему преобразования произвольного массива в максимальную кучу. Пока что мы решили только тот случай, когда есть только одна ошибка. Как это бывает, мы можем многократно использовать «случай одной ошибки» для решения всей проблемы!
Прежде всего, обратите внимание, что конечные узлы сами по себе автоматически удовлетворяют свойству max heap, поскольку у них нет дочерних узлов. Теперь рассмотрим узлы, которые находятся на один уровень выше листьев, т.е. имеют только листовые узлы как дочерние. Эти узлы могут быть не более одного шага от удовлетворения свойства max heap. Это означает, что мы можем использовать нашу функцию fix_one_error , чтобы убедиться, что все узлы, находящиеся на один уровень выше листьев, образуют кучи (или удовлетворяют свойству max heap). Теперь, когда мы переходим на другой уровень, мы знаем, что все ниже удовлетворяет свойству, поэтому мы можем снова использовать fix_one_error ! По сути, начиная чуть выше fix_one_error узлов, мы можем многократно применять fix_one_error для преобразования любого массива в кучу.
Сложность строительства кучи
Мы можем ответить довольно легко, когда нас спросят о временной сложности построения кучи. С узлами \ (n \) запустите fix_one_error на каждом узле, и сложность для каждого будет \ (O (log_2 {n}) \). Следовательно, наш алгоритм построения кучи должен быть \ (O (n \ log_2 {n}) \), верно?
Хотя это правильно, оказывается, что мы можем добиться большего успеха (то есть найти более жесткий предел)! Наша сложность для fix_one_error связана с тем, какой уровень во всем дереве начинается: чем он выше, тем больше времени он займет. На самом деле это соотношение линейно. Другими словами, fix_one_error можно охарактеризовать как \ (O (h) \), где \ (h \) — высота от fix_one_error узлов, на которых fix_one_error . Но по мере того, как мы продвигаемся выше в дереве, становится все меньше и меньше узлов. Если вы потратите время на подведение итогов ряда, который получается при анализе сложности, вы можете показать, что наш алгоритм может работать за \ (O (n) \) время.
Реализация
Хватит говорить, давайте посмотрим полную реализацию для создания кучи:
class Heap ... def create_max_heap (0..@heap_size/2-1).to_a.reverse.each do |index| fix_one_error(index) end end ... end
Вау, это довольно кратко! По сути, мы начинаем с листовых узлов, а затем постепенно продвигаемся вверх по дереву, исправляя ошибки по мере продвижения.
Операции над кучей
Давайте вернемся к нашей проблеме с электронными письмами. Скажем, у нас построена куча и мы хотим извлечь из нее элемент максимального приоритета. Просто! Просто верните первый элемент:
class Heap ... def get_max array_rep[0] end ... end
Процедура извлечения и возврата этого элемента немного сложнее, но на самом деле показывает, где светятся кучи. Мы берем последний элемент кучи и переключаем его первым (т. Е. Максимальный элемент). Таким образом, все, кроме нового первого элемента, все еще удовлетворяет свойству max heap. Теперь используйте fix_one_error на корневом узле, чтобы снова сделать массив кучей! Но перед этим уменьшите размер кучи, чтобы раз и навсегда избавиться от последнего элемента (который раньше был максимальным элементом кучи). Давайте посмотрим на это в Ruby:
class Heap ... def get_and_remove_max array_rep[@heap_size-1], array_rep[0] = array_rep[0], array_rep[@heap_size-1] @heap_size -= 1 fix_one_error(0) end ... end
Завершение
Надеюсь, вам понравился этот тур по куче (и, косвенно, очереди приоритетов) с реализациями в Ruby. Оставляйте любые вопросы в комментариях ниже!