Многие (читай: большинство) Rubyists сосредоточены на одном аспекте разработки программного обеспечения: веб-разработке. Это не обязательно плохо. Сеть растет невероятными темпами и, безусловно, является полезной (в денежном и других отношениях) областью, в которой нужно иметь опыт. Однако это не означает, что Ruby хорош только для веб-разработки.
Стандартный набор алгоритмов довольно фундаментален для информатики, и иметь небольшой опыт работы с ними может быть невероятно полезным. В этой статье мы рассмотрим некоторые из самых основных алгоритмов графа: поиск в глубину и поиск в ширину. Мы рассмотрим идеи, лежащие в их основе, где они соответствуют приложениям и их реализациям в Ruby.
терминология
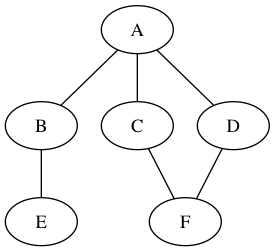
Прежде чем мы действительно сможем приступить к работе с самими алгоритмами, нам нужно немного узнать о теории графов. Если у вас раньше была теория графов в любой форме, вы можете смело пропустить этот раздел. По сути, граф — это группа узлов с некоторыми ребрами между ними (например, узлы, представляющие людей, и ребра, представляющие отношения между людьми). Что делает теорию графов особенной, так это то, что нам не особенно важна евклидова геометрическая структура узлов и ребер. Другими словами, нас не волнуют углы, которые они образуют. Вместо этого мы заботимся о «отношениях», которые создают эти края. В данный момент эта штука немного волнистая, но это станет ясно, как только мы посмотрим на некоторые конкретные примеры:
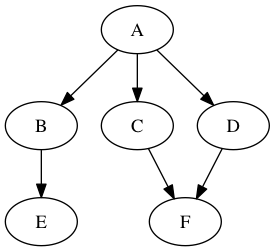
Хорошо, вот так: у нас есть график. Но что, если нам нужна структура, которая может представлять идею, что «A относится к B, но B не относится к A»? Мы можем иметь направленные ребра в графе.
Теперь есть направление, чтобы идти с каждым отношением. Конечно, мы можем создать ориентированный граф из неориентированного графа, заменив каждое неориентированное ребро двумя направленными ребрами, идущими в разные стороны.
Основная проблема
Скажем, нам дан заданный ориентированный граф (G) и два узла: (S) и (T) (обычно называемые источником и терминалом). Мы хотим выяснить, существует ли путь между (S) (T). Можем ли мы добраться до (T) по следующим ребрам (в правильном направлении) от (S) до (T)? Нас также интересует, какие узлы будут пройдены для завершения этого пути.
Существует два разных решения этой проблемы: поиск в глубину и поиск в ширину. Учитывая имена и немного воображения, легко угадать разницу между этими двумя алгоритмами.
Матрица смежности
Прежде чем мы углубимся в детали каждого алгоритма, давайте посмотрим, как мы можем представить график. Самым простым способом хранения графа является, вероятно, матрица смежности. Допустим, у нас есть граф с (V) узлами. Мы представляем этот граф с (V x V) -матрицей, полной единиц и нулей. Если существует ребро, идущее от узла [i] к узлу [j], то мы помещаем a (1) в row (i) и row (j). Если такого ребра нет, то мы помещаем a (0) в строку (i) и строку (j). Список смежности является еще одним способом представления графа. Для каждого узла (i) мы настраиваем списки, которые содержат ссылки на узлы, для которых (i) есть преимущество.
В чем разница между этими двумя подходами? Скажем, у нас есть граф с 1000 узлами, но с одним ребром. С представлением матрицы смежности нам нужно было бы выделить (1000 * 1000) массив элементов для представления графа. С другой стороны, хорошее представление списка смежности не должно было бы представлять выходные данные для всех для узлов. Однако списки смежности имеют свои недостатки. В традиционной реализации связанных списков требуется линейное время, чтобы проверить, существует ли данное ребро. Например, если мы хотим проверить, существует ли ребро (4, 6), мы должны просмотреть список выходных данных 4, а затем выполнить цикл по нему (и он может содержать все узлы на графике), чтобы проверить, если 6 является частью этого списка.
С другой стороны, проверка того, что строка 4 и столбец 6 равны 1 в матрице смежности, занимает постоянное количество времени независимо от структуры графика. Итак, если у вас есть разреженный граф (т.е. много узлов, мало ребер), используйте список смежности. Если у вас плотный граф и вы выполняете много проверок существования ребер, используйте матрицу смежности.
В оставшейся части статьи мы будем использовать матричное представление смежности главным образом потому, что об этом немного проще рассуждать.
Глубина Первый Поиск
Давайте снова посмотрим на фундаментальную проблему. По сути, мы пытаемся выяснить, можем ли мы достичь определенного узла (T) из другого узла (S). Представьте себе мышь, начинающуюся в узле (S) и кусок сыра в узле (T). Мышь может отправиться на поиски (T), следуя первому ребру, которое видит. Он продолжает делать это на каждом узле, который достигает, пока не достигнет узла, где он не может идти дальше (и до сих пор не нашел (T)). Затем он вернется к последнему узлу, где у него было другое ребро, на которое он мог бы пойти, и повторил процесс. В некотором смысле, мышь идет настолько глубоко, насколько это возможно в графике, прежде чем она возвращается. Мы называем этот алгоритм глубинным поиском .
Чтобы построить алгоритм, нам нужен какой-то способ, чтобы отслеживать, какой узел нужно возвращать, когда придет время. Чтобы облегчить это, мы используем структуру данных, называемую «стеком». Первый элемент, помещенный в стек, является первым, который покинет стек. Вот почему мы называем стек структурой LIFO (последний пришел, первый вышел) — элемент «последний вход» является элементом «первый вышел». Мышь должна удерживать стек узлов при перемещении по сети. Каждый раз, когда он достигает узла, мышь добавляет все возможные выходные данные (то есть дочерние элементы) в стек. Затем он берет первый элемент из стека (называемый «всплывающей» операцией) и перемещается на этот узел. В случае, если мы зашли в тупик (т. Е. Набор возможных выходных данных пуст), тогда операция «pop» вернет узел, на который мы можем вернуться.
Давайте рассмотрим пример глубины поиска в действии:
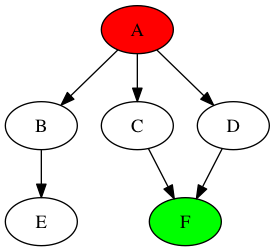
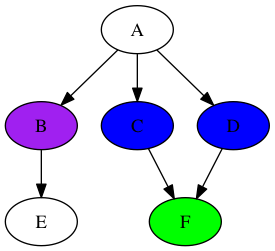
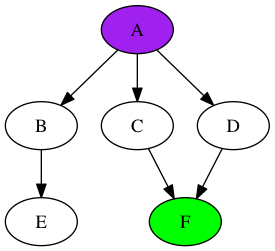
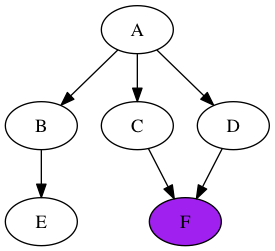
На этом графике мы имеем A в качестве исходного узла (то есть (S)) и F в качестве конечного узла (то есть (T)). Давайте добавим немного цвета на график, чтобы сделать процесс поиска более понятным. Все узлы, которые являются частью стека, окрашены в синий цвет, а узел, находящийся на вершине стека (т.е. рядом с «pop»), окрашен в фиолетовый цвет. Итак, прямо сейчас:
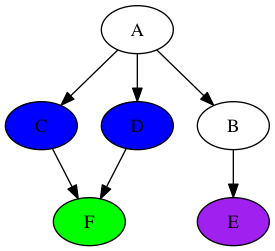
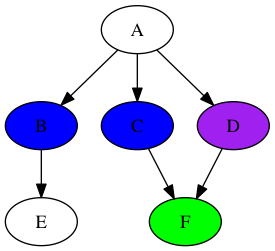
Мышь вытолкнет «A» из стека и добавит выходные данные в произвольном порядке:
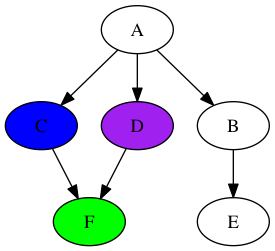
Затем мышь перемещается к узлу «B» (т.е. извлекает его из стека) и добавляет свой единственный вывод в стек:
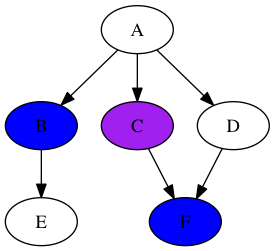
Ой-ой. Мы попали в узел без выходных узлов. К счастью, это не проблема. Мы просто выталкиваем «B», делая «D» вершиной стека:
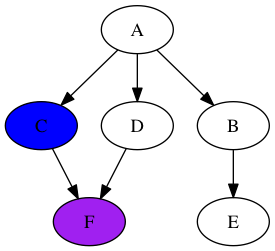
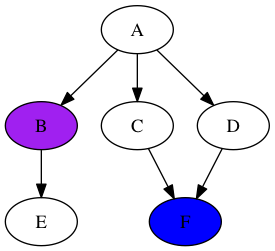
Оттуда, это всего лишь один прыжок на узел, который мы ищем! Вот окончательный результат:
Вам может быть интересно, что произойдет, если узел F не будет доступен из узла A. Просто: в какой-то момент у нас будет полностью пустой стек. Достигнув этой точки, мы знаем, что исчерпали все возможные пути из узла А.
Первый поиск в Ruby
Имея точную информацию о том, как работает поиск в глубину (т.е. DFS), посмотрите на реализацию Ruby:
def depth_first_search(adj_matrix, source_index, end_index) node_stack = [source_index] loop do curr_node = node_stack.pop return false if curr_node == nil return true if curr_node == end_index children = (0..adj_matrix.length-1).to_a.select do |i| adj_matrix[curr_node][i] == 1 end node_stack = node_stack + children end end Если вы последовали примеру, реализация должна прийти просто естественно. Давайте разберем это шаг за шагом. Прежде всего, определение метода довольно важно:
depth_first_search(adj_matrix, source_index, end_index)
Мы должны передать в adj_matrix , который является представлением матрицы смежности графа, реализованного в виде массива массивов в Ruby. Мы также предоставляем индексы исходного и конечного узлов ( source_index и end_index ) в матрице смежности.
node_stack = [source_index]
Стек начинается с исходного узла. Это можно рассматривать как отправную точку мыши. Несмотря на то, что здесь мы используем стандартный массив Ruby для нашего стека, пока реализация дает способ «выталкивать» и «выталкивать» элементы (и эти операции ведут себя так, как мы ожидаем), реализация стека не иметь значение.
loop do ... end
Код использует цикл навсегда, а затем прерывается, когда мы сталкиваемся с определенными условиями.
curr_node = node_stack.pop return false if curr_node == nil return true if curr_node == end_index
Здесь мы извлекаем текущий узел из стека и извлекаем его из цикла, если стек пуст или это искомый узел.
children = (0..adj_matrix.length-1).to_a.select do |i| adj_matrix[curr_node][i] == 1 end
Эта часть немного многословна, но цель довольно проста. Вне матрицы смежности выберите « curr_node » curr_node 1 в матрице смежности.
node_stack = node_stack + children
Возьмите эти узлы и поместите их в конец стека. Отлично! Если вы хотите быстро реализовать реализацию:
adj_matrix = [ [0, 0, 1, 0, 1, 0], [0, 0, 1, 0, 0, 1], [0, 0, 0, 1, 0, 0], [0, 0, 0, 0, 1, 1], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0] ] p depth_first_search(adj_matrix, 0, 4)
Это быстрая реализация поиска в глубину. На практике вам понадобится более сложное определение того, что такое «узел», поскольку они редко представляют собой просто индексы и к ним часто прикрепляются данные. Но общая концепция глубинного поиска остается прежней. Обратите внимание, что наша реализация работает только для ациклических графов, то есть графов, в которых нет цикла. Если мы хотим также работать с циклическими графами, нам нужно отслеживать, посещали ли мы уже узел или нет. Это довольно легкое упражнение; попробуйте реализовать это!
Ширина Первый Поиск
Что если у нас есть график, где у нас есть путь длиной 10 000 узлов, который содержит группу узлов, которые нам не нужны? Тогда, используя глубинный первый поиск, вы можете в конечном итоге пересечь этот огромный путь без всякой причины. Вот где начинается первый поиск. Вместо того, чтобы идти по пути, мы «распределяем» наш поиск по всем уровням графика. Представьте, что вы взяли кувшин с водой и налили его в узел источника. Если ребра представляют собой трубы, вода должна проходить через каждый «уровень» графика (определяемый расстоянием от исходного узла) и, возможно, достигать конечного узла.
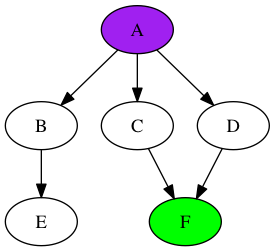
Давайте вернемся к нашей мыши, но на этот раз мы будем использовать поиск в ширину. Наш пушистый друг начнет с узла и поместит всех дочерних узлов в список. Вместо перехода к самому последнему вставленному элементу, мышь выберет «самый старый» элемент в списке. Изучение примера прояснит концепцию (опять же, на диаграммах: синий означает часть списка, фиолетовый означает следующий элемент, который должен быть удален из списка, а зеленый означает терминал). Мы начинаем так же, как поиск в глубину:
Добавьте потомков в список, но мышь теперь переместится к элементу, вставленному первым:
Теперь вот интересная часть. Мы добавляем «F» в список, но не обрабатываем его сразу, потому что «C» и «B» были добавлены ранее. Итак, вот состояние:
Удалите «С», а затем перейти к «В». Вот где разница:
Наконец, мышь может схватить сыр, когда мы возвращаемся к «F»:
Первый поиск в рубине
Структура (то есть «список»), которую мы использовали, называется «очередью». Как вы помните, стеком является LIFO (последний пришел, первый вышел). Очередь, с другой стороны, представляет собой структуру FIFO (сначала во-первых, то во-первых). Просто заменив стек на очередь в нашей реализации DFS, теперь это реализация BFS:
def breadth_first_search(adj_matrix, source_index, end_index) node_queue = [source_index] loop do curr_node = node_queue.pop return false if curr_node == nil return true if curr_node == end_index children = (0..adj_matrix.length-1).to_a.select do |i| adj_matrix[curr_node][i] == 1 end node_queue = children + node_queue end end
В этом коде есть только два важных бита.
curr_node = node_queue.pop
Обратите внимание, что мы все еще используем метод pop . Как и прежде, это возвращает последний элемент node_queue и удаляет его из массива. Тем не менее, он не дает нам последний вставленный элемент, как это было сделано для стека из-за этой строки:
node_queue = children + node_queue
Поскольку мы добавляем элементы в начало списка, взятие элемента из конца списка даст нам вставленный элемент первым, а не вставленный последним. Таким образом, незначительное изменение нашего управления списком узлов меняет поведение очереди.
Как правило, вы хотите обернуть enqueue вещи в классе или модуле и дать им enqueue и dequeue чтобы прояснить тот факт, что мы используем node_queue в качестве очереди. Здесь, опять же, поиск в ширину будет работать, только если у нас нет цикла в нашем графике. Чтобы включить графы с циклами, нам нужно отслеживать узлы, которые мы уже «открыли». Изменение реализации для этого является довольно простым и рекомендуемым упражнением.
Вывод
Надеюсь, вам понравился этот краткий обзор самых фундаментальных графовых алгоритмов в Ruby. Конечно, даже с этими мы оставили много областей раскрытыми. Например, что если вместо того, чтобы просто проверять, можем ли мы добраться до узла из источника, нам нужен путь от источника к этому узлу? Как насчет того, если мы хотим кратчайший путь? Оказывается, что DFS и BFS, приложив немного усилий, можно расширить на все виды полезных алгоритмов. В следующей статье об алгоритмах мы рассмотрим некоторые из этих «расширений».