В прошлый раз мы рассмотрели фазы «красный / зеленый / рефакторинг» разработки через тестирование (TDD). На этот раз мы подробно рассмотрим преобразования, применяемые в фазе Грина.
Приоритетное преобразование

Большинство из вас слышали о рефакторингах, которые мы применяем на последней фазе TDD, но также имеются соответствующие стандартизированные изменения кода в зеленой фазе. Дядя Боб Мартин назвал их преобразованиями .
В Приоритете Преобразования (TPP) утверждается, что эти преобразования имеют свойственный порядок, и что преобразования выбора, которые выше в списке, приводят к лучшим алгоритмам.
Неподтвержденное свидетельство представлено на примере сортировки , где нарушение порядка приводит к пузырьковой сортировке, в то время как правильный порядок приводит к быстрой сортировке.
После некоторых изменений, основанных на сообщениях других людей, дядя Боб получил следующий упорядоченный список преобразований :
| преобразование | Описание |
|---|---|
| {} -> ноль | нет кода вообще-> код, который использует ноль |
| ниль> постоянная | |
| далее константа> постоянная + | простая константа для более сложной константы |
| далее константа> скалярная | замена константы переменной или аргументом |
| Оператор-> заявления | добавив больше безусловных утверждений |
| unconditional-> если | расщепление пути выполнения |
| скалярная> массив | |
| array-> контейнер | ??? этот никогда не используется и не объясняется |
| Оператор-> хвостовой рекурсии | |
| если-> в то время как | |
| Оператор-> рекурсии | |
| expression-> функция | замена выражения на функцию или алгоритм |
| с переменной> Назначение | заменив значение переменной |
| дело | добавление регистра (или еще) к существующему коммутатору или, если |
Применение ТЭС к римским цифрам ката
Чтение чего-либо дает лишь поверхностные знания, поэтому давайте попробуем TPP на небольшой знакомой проблеме: ката римских цифр .
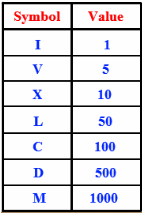
Для тех из вас, кто не знаком с этим: цель состоит в том, чтобы перевести числа на римский язык. Смотрите таблицу слева для обзора римских символов и их значений.
Как всегда в TDD, мы начнем с самого простого случая:
|
1
2
3
4
5
6
7
8
|
public class RomanNumeralsTest { @Test public void arabicToRoman() { Assert.assertEquals("i", "i", RomanNumerals.arabicToRoman(1)); }} |
Мы получаем это для компиляции с:
|
1
2
3
4
5
6
7
|
public class RomanNumerals { public static String arabicToRoman(int arabic) { return null; }} |
Обратите внимание, что мы уже применили первое преобразование в списке: {}->nil . Мы применяем второе преобразование, nil->constant , чтобы добраться до зеленого:
|
1
2
3
4
5
6
7
|
public class RomanNumerals { public static String arabicToRoman(int arabic) { return "i"; }} |
Теперь мы можем добавить наш второй тест:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
|
public class RomanNumeralsTest { @Test public void arabicToRoman() { assertRoman("i", 1); assertRoman("ii", 2); } private void assertRoman(String roman, int arabic) { Assert.assertEquals(roman, roman, RomanNumerals.arabicToRoman(arabic)); }} |
Единственный способ выполнить этот тест — ввести несколько условных ( unconditional->if ):
|
1
2
3
4
5
6
|
public static String arabicToRoman(int arabic) { if (arabic == 2) { return "ii"; } return "i";} |
Однако это приводит к дублированию между числом 2 и числом возвращаемых я. Итак, давайте попробуем другую последовательность преобразований. Предупреждение: сейчас я перехожу в режим «Детские шаги».
Сначала сделайте constant->scalar :
|
1
2
3
4
|
public static String arabicToRoman(int arabic) { String result = "i"; return result;} |
Далее, statement->statements :
|
1
2
3
4
5
|
public static String arabicToRoman(int arabic) { StringBuilder result = new StringBuilder(); result.append("i"); return result.toString();} |
Теперь мы можем ввести if без дублирования:
|
1
2
3
4
5
6
7
|
public static String arabicToRoman(int arabic) { StringBuilder result = new StringBuilder(); if (arabic >= 1) { result.append("i"); } return result.toString();} |
А потом еще одно statement->statements
|
1
2
3
4
5
6
7
8
|
public static String arabicToRoman(int arabic) { StringBuilder result = new StringBuilder(); if (arabic >= 1) { result.append("i"); arabic -= 1; } return result.toString();} |
И, наконец, мы делаем if->while :
|
1
2
3
4
5
6
7
8
|
public static String arabicToRoman(int arabic) { StringBuilder result = new StringBuilder(); while (arabic >= 1) { result.append("i"); arabic -= 1; } return result.toString();} |
Наш тест сейчас проходит. И тест на 3, кстати.
С нашей шляпой по рефакторингу мы обнаруживаем более тонкое дублирование: между числом 1 и строкой i . Они оба выражают одну и ту же концепцию (число 1), но являются разными версиями: один арабский и один римский.
Мы должны ввести класс для захвата этой концепции:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
public class RomanNumerals { public static String arabicToRoman(int arabic) { StringBuilder result = new StringBuilder(); RomanNumeral numeral = new RomanNumeral("i", 1); while (arabic >= numeral.getValue()) { result.append(numeral.getSymbol()); arabic -= numeral.getValue(); } return result.toString(); }}public class RomanNumeral { private final String symbol; private final int value; public RomanNumeral(String symbol, int value) { this.symbol = symbol; this.value = value; } public int getValue() { return value; } public String getSymbol() { return symbol; }} |
Теперь получается, что у нас есть случай с завистью к функциям . Мы можем сделать это более очевидным, извлекая метод:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
|
public static String arabicToRoman(int arabic) { StringBuilder result = new StringBuilder(); RomanNumeral numeral = new RomanNumeral("i", 1); arabic = append(arabic, result, numeral); return result.toString();}private static int append(int arabic, StringBuilder builder, RomanNumeral numeral) { while (arabic >= numeral.getValue()) { builder.append(numeral.getSymbol()); arabic -= numeral.getValue(); } return arabic;} |
Теперь мы можем переместить метод append() в RomanNumeral :
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
public class RomanNumerals { public static String arabicToRoman(int arabic) { StringBuilder result = new StringBuilder(); RomanNumeral numeral = new RomanNumeral("i", 1); arabic = numeral.append(arabic, result); return result.toString(); }}public class RomanNumeral { private final String symbol; private final int value; public RomanNumeral(String symbol, int value) { this.symbol = symbol; this.value = value; } public int getValue() { return value; } public String getSymbol() { return symbol; } public int append(int arabic, StringBuilder builder) { while (arabic >= getValue()) { builder.append(getSymbol()); arabic -= getValue(); } return arabic; }} |
Мы можем еще больше очистить, вставив получатели, которые теперь используются только в классе RomanNumeral :
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
|
public class RomanNumeral { private final String symbol; private final int value; public RomanNumeral(String symbol, int value) { this.symbol = symbol; this.value = value; } public int append(int arabic, StringBuilder builder) { while (arabic >= value) { builder.append(symbol); arabic -= value; } return arabic; }} |
В этом коде есть еще одна проблема: мы передаем arabic и builder как два отдельных параметра, но они не являются независимыми. Первый представляет часть арабского числа, еще не обработанную, в то время как последний представляет часть, которая обрабатывается. Итак, мы должны представить еще один класс для захвата общей концепции:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
|
public class RomanNumerals { public static String arabicToRoman(int arabic) { ArabicToRomanConversion conversion = new ArabicToRomanConversion(arabic); RomanNumeral numeral = new RomanNumeral("i", 1); numeral.append(conversion); return conversion.getResult(); }}public class RomanNumeral { private final String symbol; private final int value; public RomanNumeral(String symbol, int value) { this.symbol = symbol; this.value = value; } public void append(ArabicToRomanConversion conversion) { while (conversion.getRemainder() >= value) { conversion.append(symbol, value); } }}public class ArabicToRomanConversion { private int remainder; private final StringBuilder result; public ArabicToRomanConversion(int arabic) { this.remainder = arabic; this.result = new StringBuilder(); } public String getResult() { return result.toString(); } public int getRemainder() { return remainder; } public void append(String symbol, int value) { result.append(symbol); remainder -= value; }} |
К сожалению, в RomanNumeral теперь есть небольшая зависть к особенностям RomanNumeral . Мы используем conversion дважды, а наших собственных членов — три раза, так что это не так уж плохо, но давайте подумаем об этом на минутку.
Имеет ли смысл сообщать римской цифре о процессе перехода с арабского на римский? Я думаю, что нет, поэтому давайте переместим код в нужное место:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
|
public class RomanNumerals { public static String arabicToRoman(int arabic) { ArabicToRomanConversion conversion = new ArabicToRomanConversion(arabic); RomanNumeral numeral = new RomanNumeral("i", 1); conversion.process(numeral); return conversion.getResult(); }}public class RomanNumeral { private final String symbol; private final int value; public RomanNumeral(String symbol, int value) { this.symbol = symbol; this.value = value; } public String getSymbol() { return symbol; } public int getValue() { return value; }}public class ArabicToRomanConversion { private int remainder; private final StringBuilder result; public ArabicToRomanConversion(int arabic) { this.remainder = arabic; this.result = new StringBuilder(); } public String getResult() { return result.toString(); } public void process(RomanNumeral numeral) { while (remainder >= numeral.getValue()) { append(numeral.getSymbol(), numeral.getValue()); } } private void append(String symbol, int value) { result.append(symbol); remainder -= value; }} |
Нам пришлось заново ввести RomanNumeral полей RomanNumeral чтобы компилировать их. Мы могли бы избежать этой переделки, ArabicToRomanConversion класс ArabicToRomanConversion . Хм, может быть у рефакторингов тоже есть свой собственный порядок !
Хорошо, перейдем к нашему следующему тесту: 4. Мы можем сделать это с помощью другой серии преобразований. Сначала scalar->array :
|
1
2
3
4
5
6
7
8
9
|
public static String arabicToRoman(int arabic) { ArabicToRomanConversion conversion = new ArabicToRomanConversion(arabic); RomanNumeral[] numerals = new RomanNumeral[] { new RomanNumeral("i", 1) }; conversion.process(numerals[0]); return conversion.getResult();} |
Далее constant->scalar :
|
01
02
03
04
05
06
07
08
09
10
|
public static String arabicToRoman(int arabic) { ArabicToRomanConversion conversion = new ArabicToRomanConversion(arabic); RomanNumeral[] numerals = new RomanNumeral[] { new RomanNumeral("i", 1) }; int index = 0; conversion.process(numerals[index]); return conversion.getResult();} |
Теперь нам нужно, if :
|
01
02
03
04
05
06
07
08
09
10
11
12
|
public static String arabicToRoman(int arabic) { ArabicToRomanConversion conversion = new ArabicToRomanConversion(arabic); RomanNumeral[] numerals = new RomanNumeral[] { new RomanNumeral("i", 1) }; int index = 0; if (index < 1) { conversion.process(numerals[index]); } return conversion.getResult();} |
И еще одна constant->scalar
|
01
02
03
04
05
06
07
08
09
10
11
12
|
public static String arabicToRoman(int arabic) { ArabicToRomanConversion conversion = new ArabicToRomanConversion(arabic); RomanNumeral[] numerals = new RomanNumeral[] { new RomanNumeral("i", 1) }; int index = 0; if (index < numerals.length) { conversion.process(numerals[index]); } return conversion.getResult();} |
Вы, вероятно, можете увидеть, где это происходит. Далее идет statement->statements :
|
01
02
03
04
05
06
07
08
09
10
11
12
13
|
public static String arabicToRoman(int arabic) { ArabicToRomanConversion conversion = new ArabicToRomanConversion(arabic); RomanNumeral[] numerals = new RomanNumeral[] { new RomanNumeral("i", 1) }; int index = 0; if (index < numerals.length) { conversion.process(numerals[index]); index++; } return conversion.getResult();} |
Тогда if->while :
|
01
02
03
04
05
06
07
08
09
10
11
|
public static String arabicToRoman(int arabic) { ArabicToRomanConversion conversion = new ArabicToRomanConversion(arabic); RomanNumeral[] numerals = new RomanNumeral[] { new RomanNumeral("i", 1) }; for (RomanNumeral numeral : numerals) { conversion.process(numeral); } return conversion.getResult();} |
И наконец constant->constant+ :
|
01
02
03
04
05
06
07
08
09
10
11
12
|
public static String arabicToRoman(int arabic) { ArabicToRomanConversion conversion = new ArabicToRomanConversion(arabic); RomanNumeral[] numerals = new RomanNumeral[] { new RomanNumeral("iv", 4), new RomanNumeral("i", 1) }; for (RomanNumeral numeral : numerals) { conversion.process(numeral); } return conversion.getResult();} |
Теперь у нас есть завершенный алгоритм, и все, что нам нужно сделать, это добавить в массив numerals . Кстати, это должно быть константой:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
|
public class RomanNumerals { private static final RomanNumeral[] ROMAN_NUMERALS = new RomanNumeral[] { new RomanNumeral("iv", 4), new RomanNumeral("i", 1) }; public static String arabicToRoman(int arabic) { ArabicToRomanConversion conversion = new ArabicToRomanConversion(arabic); for (RomanNumeral romanNumeral : ROMAN_NUMERALS) { conversion.process(romanNumeral); } return conversion.getResult(); }} |
Кроме того, похоже, у нас есть еще один случай зависти к функциям, который мы могли бы решить следующим образом:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
public class RomanNumerals { public static String arabicToRoman(int arabic) { return new ArabicToRomanConversion(arabic).getResult(); }}public class ArabicToRomanConversion { private static final RomanNumeral[] ROMAN_NUMERALS = new RomanNumeral[] { new RomanNumeral("iv", 4), new RomanNumeral("i", 1) }; private int remainder; private final StringBuilder result; public ArabicToRomanConversion(int arabic) { this.remainder = arabic; this.result = new StringBuilder(); } public String getResult() { for (RomanNumeral romanNumeral : ROMAN_NUMERALS) { process(romanNumeral); } return result.toString(); } private void process(RomanNumeral numeral) { while (remainder >= numeral.getValue()) { append(numeral.getSymbol(), numeral.getValue()); } } private void append(String symbol, int value) { result.append(symbol); remainder -= value; }} |
ретроспективный
Первое, что я заметил, это то, что следование ТТП привело меня к открытию базового алгоритма намного быстрее, чем в некоторых из моих предыдущих попыток использовать этот ката. Следующая интересная вещь заключается в том, что между преобразованиями и рефакторингами существует взаимодействие. Вы можете либо выполнить преобразование, а затем очистить с помощью рефакторинга, или предотвратить необходимость рефакторинга, используя только те преобразования, которые не вводят дублирование. Выполнение последнего более эффективно, а также, по-видимому, ускоряет обнаружение требуемого алгоритма. Конечно, пища для размышлений. Кажется, что еще несколько экспериментов в порядке.
Ссылка: TDD и предпосылка приоритета преобразования от нашего партнера JCG Ремона Синнема в блоге по разработке безопасного программного обеспечения .