Несколько дней назад я прочитал действительно классное сообщение в блоге, объясняющее, как цепи Маркова можно использовать для моделирования возможных переходов состояний в игре змей и лестниц , об использовании цепей Маркова, о которых я даже не думал!
Хотя пример очень полезен для понимания концепции, мое понимание кода состоит в том, что он работает на предположении, что любой бросок костей, который ставит вас на счет> 100, является выигрышным броском.
В той версии игры, которую я знаю, вам нужно приземлиться ровно на 100, чтобы выиграть. Например, если вы находитесь на клетке 98 и бросаете 6, вы идете вперед на 2 пробела до 100, а затем отскакиваете на 4 пробела до 96.
Я подумал, что было бы неплохо настроить код, чтобы обслужить это:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
|
n=100 # We have 6 extra columns because we want to represent throwing of the dice which results in a final square > 100M=matrix(0,n+1,n+1+6)rownames(M)=0:ncolnames(M)=0:(n+6) # set probabilities of landing on each square assuming that there aren't any snakes or laddersfor(i in 1:6){ diag(M[,(i+1):(i+1+n)])=1/6} # account for 'bounce back' if a dice roll leads to a final score > 100for(i in 96:100) { for(c in 102:107) { idx = 101 - (c - 101) M[i, idx] = M[i, idx] + M[i, c] } } |
Мы можем проверить последние несколько строк, чтобы убедиться, что матрица перехода точна:
|
1
2
3
4
5
6
7
8
9
|
> M[95:100,95:101] 94 95 96 97 98 99 10094 0 0.1666667 0.1666667 0.1666667 0.1666667 0.1666667 0.166666795 0 0.0000000 0.1666667 0.1666667 0.1666667 0.3333333 0.166666796 0 0.0000000 0.0000000 0.1666667 0.3333333 0.3333333 0.166666797 0 0.0000000 0.0000000 0.1666667 0.3333333 0.3333333 0.166666798 0 0.0000000 0.1666667 0.1666667 0.1666667 0.3333333 0.166666799 0 0.1666667 0.1666667 0.1666667 0.1666667 0.1666667 0.1666667 |
Если мы находимся на 99-м квадрате (последний ряд), мы можем бросить 1 и в итоге на 100, 2 и в итоге на 99 (1 вперед, 1 назад), 3 и в конечном итоге на 98 (1 вперед, 2 назад), 4 и заканчиваются на 97 (1 вперед, 3 назад), 5 и заканчиваются на 96 (1 вперед, 4 назад) или 6 и заканчиваются на 95 (1 вперед, 5 назад). то есть мы можем приземлиться на 95, 96, 97, 98, 99 или 100 с вероятностью 1/6.
Если мы находимся на 96-м квадрате (3-й ряд), мы можем бросить 1 и в итоге на 97, 2 и в итоге на 98, 3 и в итоге на 99, 4 и в итоге на 100, 5 и в конечном итоге на 99 (4 вперед, 1 назад) или 6 и в конечном итоге на 98 (4 вперед, 2 назад). то есть мы можем приземлиться на 97 с вероятностью 1/6, 98 с вероятностью 2/6, 99 с вероятностью 2/6 или 100 с вероятностью 1/6.
Мы могли бы сделать аналогичный анализ для других квадратов, но кажется, что вероятности рассчитываются правильно.
Далее мы можем обновить матрицу со змеями и лестницами. Этот код остается прежним:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
|
# get rid of the extra columns, we don't need them anymoreM=M[,1:(n+1)] # add in the snakes and laddersstarting = c(4,9,17,20,28,40,51,54,62,64,63,71,93,95,92)ending = c(14,31,7,38,84,59,67,34,19,60,81,91,73,75,78) for(i in 1:length(starting)) { # Retrieve current probabilities of landing on the starting square v=M[,starting[i]+1] ind=which(v>0) # Set no probability of falling on the starting squares M[ind,starting[i]+1]=0 # Move all existing probabilities to the ending squares M[ind,ending[i]+1]=M[ind,ending[i]+1]+v[ind]} |
Мы также можем упростить функцию powermat, которая используется для имитации того, как будет выглядеть доска после определенного количества бросков костей:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
|
# originalpowermat=function(P,h){ Ph=P if(h>1) { for(k in 2:h) { Ph=Ph%*%P } } return(Ph)} #newlibrary(expm)powermat = function(P,h) { return (P %^% h)} |
|
1
2
3
4
5
6
7
|
initial=c(1,rep(0,n))h = 1> (initial%*%powermat(M,h))[1:15] 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45[1,] 0 0.1666667 0.1666667 0.1666667 0 0.1666667 0.1666667 0 0 0 0 0 0 0 0.1666667 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100[1,] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
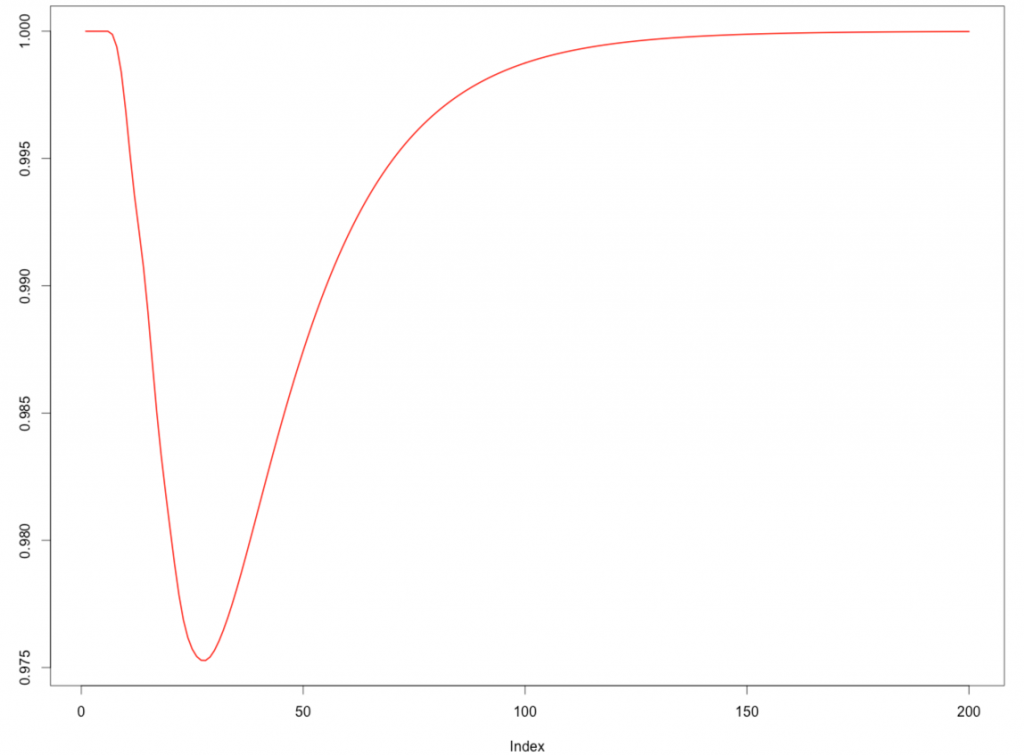
Одна интересная вещь, которую я заметил, заключается в том, что теперь для завершения игры в среднем требуется больше ходов, чем когда вам не нужно было набирать ровно 100 очков, чтобы выиграть:
|
1
2
|
> sum(1 - game)[1] 999 |
|
1
2
3
4
5
6
7
|
distrib=initial%*%Mgame=rep(NA,1000)for(h in 1:length(game)){game[h]=distrib[n+1]distrib=distrib%*%M}plot(1-game[1:200],type="l",lwd=2,col="red",ylab="Probability to be still playing") |
Я ожидал, что это займет больше времени, чтобы закончить игру, но не так долго! Я думаю, что, вероятно, ошибся, но я не уверен, где …
Обновить
Антониос обнаружил ошибку, которую я сделал — когда на 100-м квадрате у нас должна быть 1 как вероятность попасть на 100-й квадрат. т.е. нам нужно обновить M примерно так:
|
1
|
M[101,101] = 1 |
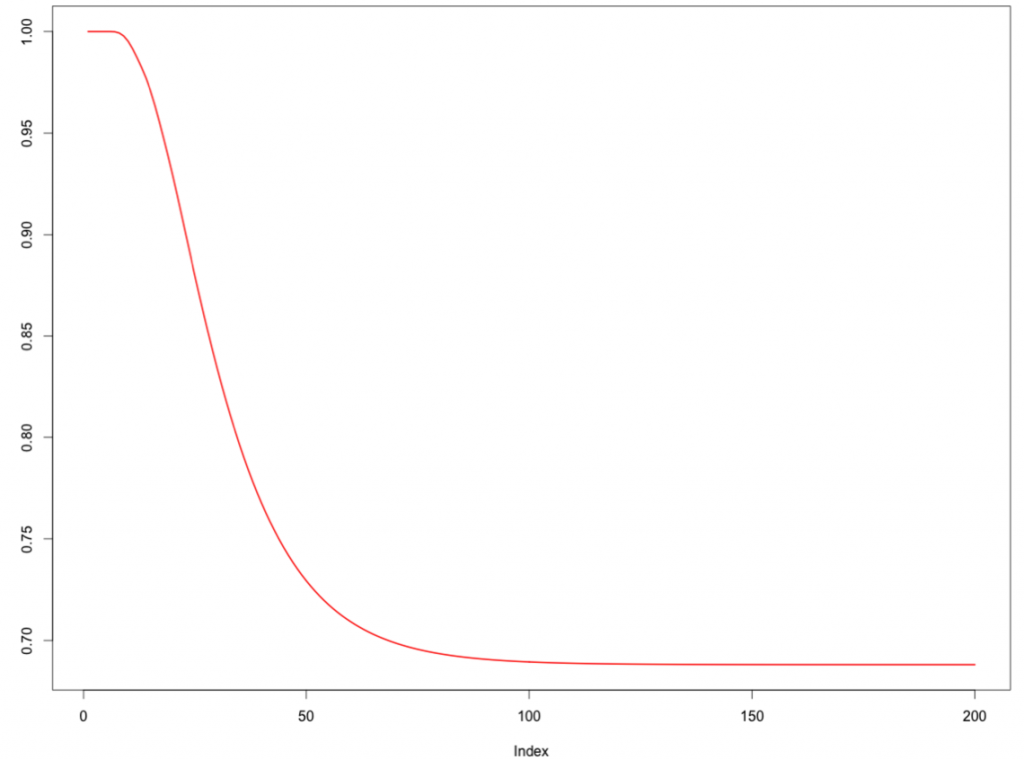
Теперь, если мы представим, что он все еще играет, мы получим более точную кривую:
|
1
2
3
4
5
6
7
|
distrib=initial%*%Mgame=rep(NA,1000)for(h in 1:length(game)){game[h]=distrib[n+1]distrib=distrib%*%M}plot(1-game[1:200],type="l",lwd=2,col="red",ylab="Probability to be still playing") |
| Ссылка: | Р: Марковская сеть Snakes and ladders от нашего партнера JCG Марка Нидхэма в блоге Марка Нидхэма . |