В предыдущих статьях мы обсуждали различные методы машинного обучения, в том числе линейную регрессию с регуляризацией, SVM, нейронную сеть, ближайший сосед, наивный байесовский алгоритм, модели дерева решений и ансамбля. Как мы выбираем, какая модель лучше? или даже лучше ли выбранная нами модель, чем случайное предположение? В этих постах мы расскажем, как мы оцениваем производительность модели и что мы можем делать дальше, чтобы улучшить производительность.
Лучшая догадка без модели
Прежде всего, нам нужно понять цель нашей оценки. Мы пытаемся выбрать лучшую модель? Мы пытаемся количественно оценить улучшение каждой модели? Независимо от нашей цели я обнаружил, что всегда полезно подумать о том, какой должна быть базовая линия. Обычно базовый уровень — это то, что вы считаете наиболее вероятным, если у вас нет модели.
Для задачи классификации один из подходов состоит в том, чтобы сделать случайное предположение (с равномерной вероятностью), но лучший подход состоит в том, чтобы угадать выходной класс, который имеет наибольшую долю в обучающих выборках. Для задачи регрессии лучшим предположением будет среднее значение выходных обучающих выборок.
Подготовить данные для оценки
В типичном случае набор данных делится на 3 непересекающиеся группы; Данные 20% откладываются в качестве данных тестирования для оценки модели, которую мы обучили. Оставшиеся 80% данных делятся на k разделов. k-1 разделы будут использоваться в качестве обучающих данных для обучения модели с настройкой определенного значения параметра, а 1 раздел будет использоваться в качестве данных перекрестной проверки для выбора наилучшего значения параметра, минимизирующего ошибку данных перекрестной проверки.
В качестве конкретного примера, скажем, у нас есть 100 доступных записей. Мы выделим 20%, что составляет 20 записей для целей тестирования, и используем оставшиеся 80 записей для обучения модели. Допустим, модель имеет некоторые настраиваемые параметры (например, k в KNN, λ в регуляризации линейной модели). Для каждого конкретного значения параметра мы проведем 10 раундов обучения (т.е.: k = 10). В каждом раунде мы случайным образом выбираем 90%, что составляет 72 записи, чтобы обучить модель и вычислить ошибку прогнозирования по 8 невыбранным записям. Затем мы берем среднюю ошибку этих 10 раундов и выбираем оптимальное значение параметра, которое дает минимальную среднюю ошибку. После выбора оптимального параметра настройки мы переобучаем модель, используя целых 80 записей.
Чтобы оценить прогнозирующую производительность модели, мы проверим ее по 20 записям тестирования, которые мы откладывали в начале. Детали будут описаны ниже.
Измерение производительности регрессии
Для задачи регрессии измерение расстояния между расчетным выходом и фактическим выходом используется для количественной оценки производительности модели. Обычно используются три показателя: среднеквадратическая ошибка, относительная квадратная ошибка и коэффициент определения. Обычно среднеквадратичное значение используется для измерения абсолютной величины точности.
Среднеквадратическая ошибка MSE = (1 / N) * ∑ (
прошлый —
фактический )
2
ошибка
RMSE = (MSE)
1/2
Чтобы измерить точность относительно базовой линии, мы используем соотношение MSE
Относительная квадратная ошибка RSE = MSE / MSE
baseline
yst — y
фактическое )
2 / ∑ (y
среднее — y
фактическое )
2
Коэффициент определения (также называемый квадрат R) измеряет дисперсию, которая объясняется моделью, которая представляет собой уменьшение дисперсии при использовании модели. Квадрат R колеблется от 0 до 1, в то время как модель обладает сильной предсказательной силой, когда она близка к 1, и ничего не объясняет, когда она близка к 0.
R
2 = (
базовый уровень MSE — MSE) / базовый уровень MSE
Вот некоторый код R для вычисления этих мер
> > Prestige_clean <- Prestige[!is.na(Prestige$type),] > model <- lm(prestige~., data=Prestige_clean) > score <- predict(model, newdata=Prestige_clean) > actual <- Prestige_clean$prestige > rmse <- (mean((score - actual)^2))^0.5 > rmse [1] 6.780719 > mu <- mean(actual) > rse <- mean((score - actual)^2) / mean((mu - actual)^2) > rse [1] 0.1589543 > rsquare <- 1 - rse > rsquare [1] 0.8410457 >
Ошибка среднего квадрата штрафует большую разницу больше из-за эффекта квадрата. С другой стороны, если мы хотим уменьшить штраф за большую разницу, мы можем сначала преобразовать числовое значение в лог.
Среднеквадратичная ошибка журнала MSLE = (1 / N) * ∑ (log (y)
est — log (y)
фактическая )
2
ошибка журнала
RMSLE = (MSLE)
1/2
Измерение эффективности классификации
Для классификации проблемы есть несколько мер.
- TP = прогноз + ве, когда факт + ве
- TN = предсказать -ve, когда фактический -ve
- FP = Predict + ve, когда Actual -ve
- FN = предсказать -ve когда фактический + ve
Точность = TP / Прогноз + ve = TP / (TP + FP)
Отзыв или чувствительность = TP / Фактический + ve = TP / (TP + FN)
Специфичность = TN / Actual -ve = TN / (FP + TN)
Точность = ( TP + TN) / (TP + TN + FP + FN)
Одной точности недостаточно для представления качества прогноза, поскольку стоимость создания FP может отличаться от стоимости создания FN. F меры обеспечивает настраиваемый назначенный вес для вычисления окончательной оценки и обычно используется для измерения качества модели классификации.
1 / Fmeasure = α / отзыв + (1-α) / точность
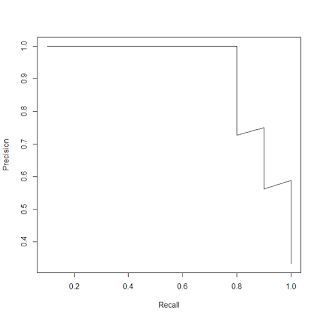
Обратите внимание, что большая часть модели классификации основана на оценке числовой оценки для каждого выходного класса. Выбирая точку отсечения этой оценки, мы можем контролировать компромисс между точностью и отзывом. Мы можем построить соотношение между точностью и отзывом в различных точках отсечения следующим образом …
> library(ROCR)
> library(e1071)
> nb_model <- naiveBayes(Species~., data=iristrain)
> nb_prediction <- predict(nb_model,
iristest[,-5],
type='raw')
> score <- nb_prediction[, c("virginica")]
> actual_class <- iristest$Species == 'virginica'
> # Mix some noise to the score
> # Make the score less precise for illustration
> score <- (score + runif(length(score))) / 2
> pred <- prediction(score, actual_class)
> perf <- performance(pred, "prec", "rec")
> plot(perf)
>
Другим распространенным графиком является кривая ROC, которая отображает «чувствительность» (истинно положительный показатель) против 1 — «специфичность» (ложно положительный показатель). Область под кривой «auc» используется для сравнения качества между различными моделями с различными точками среза. Вот как мы получаем кривую ROC.
> library(ROCR)
> library(e1071)
> nb_model <- naiveBayes(Species~.,
data=iristrain)
> nb_prediction <- predict(nb_model,
iristest[,-5],
type='raw')
> score <- nb_prediction[, c("virginica")]
> actual_class <- iristest$Species == 'virginica'
> # Mix some noise to the score
> # Make the score less precise for illustration
> score <- (score + runif(length(score))) / 2
> pred <- prediction(score, actual_class)
> perf <- performance(pred, "tpr", "fpr")
> auc <- performance(pred, "auc")
> auc <- unlist(slot(auc, "y.values"))
> plot(perf)
> legend(0.6,0.3,c(c(paste('AUC is', auc)),"\n"),
border="white",cex=1.0,
box.col = "white")
>
Мы также можем назначить относительную стоимость принятия ложного + ve и ложного-ve решения, чтобы найти наилучший порог отсечки. Вот как мы строим кривую стоимости
> # Plot the cost curve to find the best cutoff > # Assign the cost for False +ve and False -ve > perf <- performance(pred, "cost", cost.fp=4, cost.fn=1) > plot(perf) >
Из кривой, лучшая точка отсечения 0,6, где стоимость минимальна.
Источник ошибки: смещение и дисперсия
В основанном на модели машинном обучении мы предполагаем, что базовые данные следуют некоторой базовой математической модели, и во время обучения мы пытаемся вписать обучающие данные в эту предполагаемую модель и определить наилучшие параметры модели, которые дают минимальную ошибку.
Один из источников ошибок — это когда наша предполагаемая модель в корне неверна (например, если выход имеет нелинейную связь с входом, но мы предполагаем линейную модель). Это известно как проблема высокого смещения, которую мы используем для упрощения представления упрощенной модели.
Другим источником ошибки является то, что параметры модели слишком точно соответствуют обучающим данным и плохо обобщаются на базовый шаблон данных. Это известно как проблема высокой дисперсии и обычно возникает, когда недостаточно обучающих данных, сравниваемых с количеством параметров модели.
Проблема высокого смещения имеет признак того, что как при обучении, так и при перекрестной проверке наблюдается высокая частота ошибок, и частота ошибок уменьшается по мере увеличения сложности модели. В то время как ошибка обучения продолжает уменьшаться по мере увеличения сложности модели, ошибка перекрестной проверки будет увеличиваться после определенной сложности модели, и это указывает на начало проблемы с высокой дисперсией. Когда размер обучающих данных фиксирован, и единственное, что мы можем выбрать, — это сложность модели, тогда мы должны выбрать сложность модели в точке, где ошибка перекрестной проверки минимальна.
Поможет ли получить больше данных?
При сборе большего количества данных, как времени, так и денег, мы должны тщательно оценить ситуацию, прежде чем затрачивать на это наши усилия. Эндрю Нг из Стэнфорда предложил очень прагматичную методику, отображающую ошибку в зависимости от размера данных. В этом подходе мы выбираем различный размер данных обучения для обучения разных моделей и наносим на график как ошибку перекрестной проверки, так и ошибку обучения относительно размера обучающей выборки.
Если проблема связана с высоким смещением, кривая ошибки будет выглядеть следующим образом.
В этом случае сбор дополнительных данных не поможет. Мы должны потратить наши усилия, чтобы сделать следующее.
- Добавьте больше возможностей ввода, поговорив с экспертами по предметной области, чтобы определить больше входных сигналов и собрать их.
- Добавьте дополнительные функции ввода, комбинируя существующие функции ввода нелинейным способом.
- Попробуйте более сложные модели машинного обучения. (например, увеличить количество скрытых слоев в нейронной сети или увеличить количество нейронов на каждом слое)
Если проблема является проблемой высокой дисперсии, потому что мы переоцениваем сложность модели, то мы должны уменьшить сложность модели, отбрасывая атрибуты, которые имеют низкое влияние на результат. Нам не нужно собирать больше данных.
Единственная ситуация, когда полезно иметь больше данных, — это когда базовая модель данных действительно сложна. Поэтому мы не можем просто уменьшить сложность, так как это немедленно приведет к проблеме с большим смещением. В этом случае кривая ошибки будет иметь следующую форму.
И единственный способ состоит в том, чтобы собрать больше данных о тренировках, чтобы вероятность переобучения была меньше.
Оценка эффективности модели очень важна в общем цикле прогнозной аналитики. Надеемся, что этот вводный пост дает основную идею о том, как это можно сделать.