Это короткий отрывок из главы 5 (Коллекции и обобщения) Pro Pro. Performance , которая должна появиться в августе 2012 года. Возможно, я опубликую еще несколько из них до и после выхода книги.
Выбор правильной коллекции касается не только ее производительности. Способ размещения данных в памяти часто более критичен для приложений, связанных с ЦП, чем любой другой критерий, и коллекции сильно влияют на этот макет. Основным фактором тщательного изучения размещения данных в памяти является кэш-память процессора.
Современные системы поставляются с большими основными воспоминаниями. Восемь ГБ памяти достаточно стандартно для рабочей станции среднего класса или игрового ноутбука. Блоки памяти Fast DDR3 SDRAM имеют задержку доступа к памяти около 15 нс и теоретическую скорость передачи около 15 ГБ / с. Быстрые процессоры, с другой стороны, могут выдавать миллиарды инструкций в секунду; теоретически, остановка на 15 нс в ожидании доступа к памяти может помешать выполнению десятков (а иногда и сотен) инструкций процессора. Задержка доступа к памяти — явление, известное как удар по стене памяти .
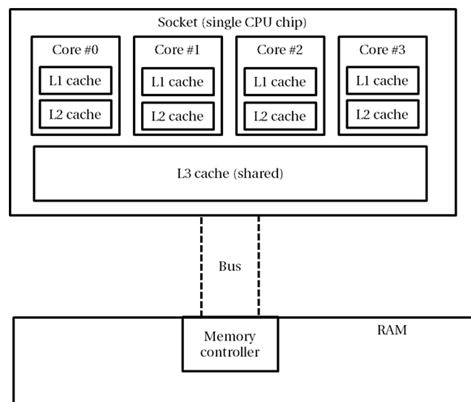
Чтобы дистанцировать приложения от этой стены, современные процессоры оснащены несколькими уровнями кэш-памяти , которая имеет внутренние характеристики, отличные от основной памяти, и, как правило, очень дорогая и относительно небольшая. Например, процессор Intel i7-860 моего компьютера поставляется с тремя уровнями кэша:
- Кэш 1-го уровня для программных инструкций, 32 КБ, по одному на каждое ядро (всего 4 кеша).
- Кэш 1-го уровня для данных, 32 КБ, по одному для каждого ядра (всего 4 кеша).
- Кэш 2-го уровня для данных, 256 КБ, по одному на каждое ядро (всего 4 кеша).
- Кэш 3-го уровня для данных, 8 МБ, общий (всего 1 кэш).
Когда процессор пытается получить доступ к адресу памяти, он начинает с проверки того, находятся ли данные в его кэше L1. Если это так, доступ к памяти выполняется из кеша, что занимает ~ 5 циклов ЦП (это называется попаданием в кеш ). Если это не так, проверяется кэш L2; Удовлетворение доступа из кэша L2 занимает около 10 циклов. Аналогично, для удовлетворения доступа из кэша L3 требуется около 40 циклов. Наконец, если данные не находятся ни на одном из уровней кэша, процессор остановится для основной памяти системы (это называется отсутствием кэша ). Когда процессор обращается к основной памяти, он читает из него не один байт или слово, а строку кэша, который в современных системах состоит из 32 или 64 байтов. Доступ к любому слову в той же строке кэша не повлечет за собой повторного пропуска кэша, пока строка не будет удалена из кэша.
Чтобы рассчитать задержки доступа к кэшу на реальном оборудовании, вы можете обратиться к спецификациям оборудования или использовать живую утилиту для тестирования производительности, такую как инструмент вычисления задержки CPUID . Вот пример его вывода на моем настольном ПК:
Cache latency computation, ver 1.0 www.cpuid.com Computing ... <diagnostic output skipped> 3 cache levels detected Level 1 size = 32Kb latency = 3 cycles Level 2 size = 256Kb latency = 10 cycles Level 3 size = 8192Kb latency = 39 cycles
Хотя это описание не отражает истинную аппаратную сложность работы кэшей SRAM и памяти DRAM, оно дает достаточную информацию для размышлений и обсуждения того, как на наши программные алгоритмы высокого уровня может повлиять размещение данных в памяти. Теперь рассмотрим простой пример, который включает кеш одного ядра. (Есть интересные случаи, когда нужно рассмотреть, где задействованы несколько кешей из разных ядер — глава 6 книги описывает их более подробно.)
Предположим, что задача состоит в том, чтобы обойти большую коллекцию целых чисел и выполнить некоторую их агрегацию, например найти их сумму или среднее значение. Ниже приведены две альтернативы; один обращается к данным из LinkedList <int>, а другой — из массива целых чисел ( int [] ), двух из встроенных коллекций .NET.
LinkedList<int> numbers = new LinkedList<int>(
Enumerable.Range(0, 20000000));
int sum = 0;
for (LinkedListNode<int> curr = numbers.First;
curr != null; curr = curr.Next)
{
sum += curr.Value;
}
int[] numbers = Enumerable.Range(0, 20000000).ToArray();
int sum = 0;
for (int curr = 0; curr < numbers.Length; ++curr)
{
sum += numbers[curr];
}
Вторая версия кода работает в 2 раза быстрее, чем первая на моем рабочем столе. Это существенная разница, и если вы учитываете только количество выпущенных инструкций процессора, вы можете не быть уверены, что разница должна быть вообще. В конце концов, обход связанного списка включает в себя переход от одного узла к другому, а обход массива — увеличение индекса в массив. (На самом деле, без JIT-оптимизации доступ к элементу массива потребовал бы также проверки диапазона, чтобы убедиться, что индекс находится в пределах массива.)
; possible x86 assembly for the first loop ; assume ‘sum’ is in EAX and ‘numbers’ is in ECX xor eax, eax mov ecx, dword ptr [ecx+4] ; curr = numbers.First test ecx, ecx jz LOOP_END LOOP_BEGIN: add eax, dword ptr [ecx+10] ; sum += curr.Value mov ecx, dword ptr [ecx+8] ; curr = curr.Next test ecx, ecx jnz LOOP_BEGIN ; total of 4 instructions per iteration LOOP_END: ... ; possible x86 assembly for the second loop ; assume ‘sum’ is in EAX and ‘numbers’ is in ECX mov edi, dword ptr [ecx+4] ; numbers.Length test edi, edi jz LOOP_END xor edx, edx ; loop index LOOP_BEGIN: add eax, dword ptr [ecx+edx*4+8] ; sum += numbers[i] inc edx cmp esi, edx jg LOOP_BEGIN ; total of 4 instructions per iteration LOOP_END: ...
Учитывая это генерирование кода для обоих циклов (и оптимизацию запрета, такую как использование SIMD-инструкций для обхода массива, который является непрерывным в памяти), трудно объяснить существенную разницу в производительности, проверяя только выполненные инструкции. Действительно, мы должны проанализировать шаблоны доступа к памяти этого кода, чтобы сделать какие-либо приемлемые выводы.
В обоих циклах к каждому целому числу обращаются только один раз, и может показаться, что соображения о кеше не столь критичны, потому что нет данных многократного использования, чтобы извлечь выгоду из обращений к кешу. Тем не менее, способ размещения данных в памяти сильно влияет на производительность этой программы — не потому, что данные используются повторно, а из-за того, как они заносятся в память. При доступе к элементам массива пропадание кэша в начале строки кэша приводит к попаданию в кэш 16 последовательных целых чисел (строка кэша = 64 байта = 16 целых чисел). Поскольку доступ к массиву является последовательным, следующие 15 целых чисел теперь находятся в кэше и могут быть доступны без промаха кэша. Это почти идеальный сценарий с коэффициентом пропадания кэша 1:16. С другой стороны, при доступе к элементам связанного списка, пропадание кеша в начале строки кеша может привести к кешуне более 3 последовательных узлов связанного списка, коэффициент пропуска кэша 1: 4! (Узел состоит из обратного указателя, прямого указателя и целочисленных данных, которые занимают 12 байтов в 32-битной системе; заголовок ссылочного типа приводит к подсчету до 20 байтов на узел.)
Гораздо более высокий коэффициент пропадания кэша является причиной большей разницы в производительности между двумя фрагментами кода, которые мы тестировали выше. Кроме того, мы предполагаем идеальный сценарий, при котором все узлы связанного списка располагаются последовательно в памяти, что будет иметь место только в том случае, если они были распределены одновременно без других распределений, и это довольно маловероятно. Если бы узлы связанного списка распределялись в памяти менее идеально, коэффициент пропадания кэша был бы еще выше, а производительность была бы еще ниже.
Более практичные примеры — и все, что вы когда-либо захотите узнать о кэшах ЦП и соображениях производительности системной памяти — описаны в прекрасном эссе Ульриха Дреппера «Что каждый программист должен знать о памяти» . Я рекомендую перечитывать эту статью хотя бы раз в год ?