График распределения степеней с использованием R над Hadoop

Существует два распространенных типа графических движков. Один тип ориентирован на предоставление алгоритмов прохождения в реальном времени по графам связанных списков, представленных на одном сервере. Такие механизмы обычно называют графовыми базами данных, и некоторые из поставщиков включают Neo4j , OrientDB , DEX и InfiniteGraph . Другой тип графического движка ориентирован на пакетную обработку с использованием вершинно-ориентированных сообщений, передаваемых в графе, представленном в кластере машин. Графовые движки этой формы включают в себя Hama , Golden Orb , Giraph и Pregel .

Цель этого поста — показать, как выразить вычисление двух основных статистических графов — каждый в виде обхода графа и алгоритма MapReduce . Для этой цели были использованы графические движки Neo4j и Hadoop . Однако, что касается Hadoop, вместо того, чтобы сосредотачиваться на конкретном вершинно-ориентированном BSP -пакете для обработки графов, таком как Hama или Giraph, представленные результаты получены с помощью собственного Hadoop (HDFS + MapReduce). Более того, вместо разработки алгоритмов MapReduce в Java используется язык программирования R. RHadoop — это небольшой пакет с открытым исходным кодом, разработанный Revolution Analytics, который связывает R с Hadoop и позволяет представлять алгоритмы MapReduce с использованием нативного R.

Два графовых алгоритма представляют статистику степеней вычислений: степень вершины и распределение степени графа . Оба связаны, и фактически результаты первого могут использоваться как входные данные для второго. То есть распределение графа по степени является функцией вершины по степени. Вместе эти две фундаментальные статистики служат основой для более количественной статистики, разработанной в областях теории графов и сетевой науки .

1. Вершинная степень : сколько входящих ребер имеет вершина X ?
2. Распределение графа в градусах : Сколько вершин имеют число входных ребер по X ?

Эти два алгоритма рассчитываются на основе искусственно созданного графа, который содержит 100 000 вершин и 704 002 ребер. Подмножество изображено слева. Алгоритм, используемый для генерации графа, называется преимущественным вложением . Преимущественное вложение дает графы с «естественной статистикой», которые имеют распределения степеней, аналогичные реальным графам / сетям. Соответствующий код iGraph R приведен ниже. После построения и упрощения (т. Е. Не более одного ребра между любыми двумя вершинами и без самопетлей) вершины и ребра считаются. Затем первые пять ребер повторяются и отображаются. Первое ребро гласит: «Вершина 2 соединена с вершиной 0.» Наконец, график сохраняется на диске в виде файла GraphML .

График статистики с использованием Neo4j

Когда граф порядка 10 миллиардов элементов (вершины + ребра), тогда для выполнения анализа графа достаточно базы данных с одним сервером. В качестве примечания, когда эти аналитики / алгоритмы являются «эгоцентричными» (то есть, когда обход исходит от одной вершины или небольшого набора вершин), тогда они обычно могут оцениваться в режиме реального времени (например, <1000 мс). Для вычисления этих статистических данных используется Gremlin . Gremlin — это язык обхода графов, разработанный TinkerPop, который распространяется с Neo4j, OrientDB, DEX, InfiniteGraph и движком RDF Stardog . Код Gremlin ниже загружает файл GraphML, созданный R в предыдущем разделе, в Neo4j. Затем выполняется подсчет вершин и ребер графа.

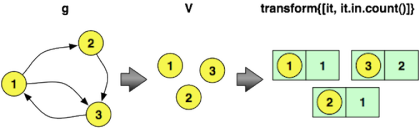
Код Гремлин для вычисления вершины в градусах приведен ниже. Первая строка перебирает все вершины и выводит вершину и ее степень. Вторая строка предоставляет фильтр диапазона для отображения только первых пяти вершин и их количества в градусах. Обратите внимание, что поясняющие диаграммы демонстрируют преобразования на игрушечном графе, а не на графе 100 000 вершин, использованном в эксперименте.

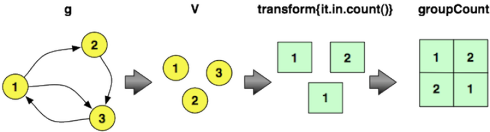
Затем, чтобы вычислить распределение графа в градусах, можно выполнить следующий обход Гремлин. Это выражение перебирает все вершины графа, выдает их в градусах, а затем подсчитывает, сколько раз встречается конкретный градус. Эти подсчеты сохраняются во внутренней карте, поддерживаемой groupCount . Последний шаг cap дает внутреннюю карту groupCount . Чтобы отображать только первые пять отсчетов, применяется фильтр диапазона. В первой строке написано: «Есть 52 611 вершин, у которых нет входящих ребер». Вторая строка гласит: «16 168 вершин имеют одно входящее ребро».

Чтобы вычислить обе статистики, используя результаты предыдущего вычисления в последнем, можно выполнить следующий обход. Это представление имеет прямую корреляцию с тем, как вычисляется вершина в градусах и график в градусах с использованием MapReduce (продемонстрировано в следующем разделе).

График статистики с использованием Hadoop

Когда граф порядка 100+ миллиардов элементов (вершины + ребра), тогда база данных графа с одним сервером не сможет представлять или обрабатывать граф. Требуется много-машинный графовый движок. Хотя нативный Hadoop не является графическим механизмом, граф может быть представлен в его распределенной файловой системе HDFS и обработан с использованием инфраструктуры распределенной обработки MapReduce. Ранее сгенерированный граф загружается в R и проводится подсчет его вершин и ребер. Далее график представляется в виде списка ребер. Список ребер (для однореляционного графа) — это список пар, где каждая пара упорядочена и обозначает идентификатор хвостовой вершины и идентификатор головной вершины ребра. Список границ может быть передан в HDFS с помощью RHadoop. Переменная edge.list представляет указатель на этот файл HDFS.

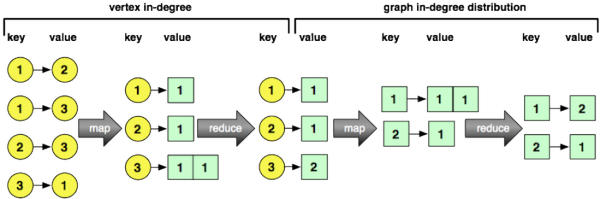
Для вычисления вершины в edge.list задание MapReduce оценивается в edge.list . Функция map подается парам ключ / значение, где ключ — это идентификатор ребра, а значение — это идентификаторы хвостовой и головной вершин ребра (представленные в виде списка). Для каждого ввода ключ / значение, верхняя вершина (т. Е. Входящая вершина) испускается вместе с номером 1. Функция сокращения подает пары ключ / значение, где ключи — вершины, а значения — список из 1 с. Выходные данные задания сокращения — это идентификатор вершины и длина списка 1 с (т. Е. Сколько раз эта вершина рассматривалась как входящая / головная вершина ребра). Результаты этого задания MapReduce сохраняются в HDFS, а degree.V — указатель на этот файл. Последнее выражение в фрагменте кода ниже считывает первую пару ключ / значение из степени. degree.V — вершина 10030 имеет степень 5.

Чтобы вычислить распределение графа в degree.V задание MapReduce оценивается по degree.V . Функция карты подается на результаты ключ / значение, хранящиеся в degree.V . Функция выдает степень вершины с номером 1 в качестве значения. Например, если вершина 6 имеет степень в 100, то функция карты выдает ключ / значение [100,1]. Затем, функция уменьшения представляет собой клавиши, которые представляют градусы со значениями, которые представляют собой число раз, когда градус рассматривался как список из 1 с. Вывод функции Reduce является ключом вместе с длиной списка 1 с (т. Е. Сколько раз встречался градус определенного подсчета). Последний фрагмент кода ниже захватывает первую пару ключ / значение из degree.g — степень 1354 встречалась 1 раз.

Вместе эти два вычисления могут быть объединены в одно выражение MapReduce.

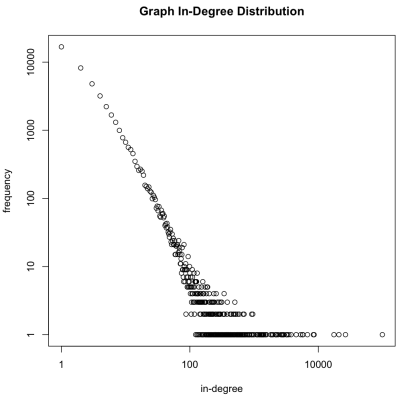
Обратите внимание, что хотя граф может иметь порядок более 100 миллиардов элементов, распределение степеней намного меньше и обычно может помещаться в память. В общем, edge.list > degree.V > degree.g . Из-за этого факта можно degree.g файл degree.g из HDFS, поместить его в основную память и вывести на degree.g результаты, сохраненные в нем. Распределение degree.g построено на графике / журнале . Как и предполагалось, алгоритм предпочтительного присоединения генерировал граф с естественной « безмасштабной » статистикой — большинство вершин имеют небольшую степень и очень немногие имеют большую степень.

Связанные материалы

• Коэн, Дж., « Поворот графика в мире MapReduce» , «Компьютеры в науке и технике», IEEE, 11 (4), с. 29-41, июль 2009