Это глубокое погружение в криптографию было первоначально опубликовано на сайте Бруно в Bitfalls и воспроизводится здесь с разрешения.
Средства массовой информации забиты контентом о криптовалюте, и все бушуют о важности открытых и закрытых ключей. Вы слышали о шифровании, но знаете ли вы, что это такое и как оно работает?
Этот пост вернет вас к основам и объяснит шифрование , опишет различные типы и продемонстрирует примеры алгоритмов, все для новичков. Если вы когда-нибудь хотели понять это, но это казалось слишком сложным, вам понравится этот пост.
криптография
Криптография, в двух словах, превращает сообщение в такой формат, который имеет смысл только для получателя, а не для любого, кто мог бы получить его между ними.
Какую проблему мы пытаемся решить?
Предположим, есть два человека, которые хотят обмениваться зашифрованными сообщениями, независимо от канала связи, который они используют — письма, SMS, электронная почта … Сначала они должны прийти к соглашению о наборе правил, которые должны применяться при шифровании или дешифровании сообщения. Эти правила представляют собой набор из одной или нескольких функций, которые должны иметь контрфункцию . То есть, если данная функция используется для шифрования сообщения, то должна существовать контрфункция для его дешифрования. На математическом языке такая функция является биективной .
Отправитель сообщения применяет функцию к набору информации и получает зашифрованную версию этой информации, которая затем может быть отправлена получателю. Получатель применяет контрфункцию для извлечения достоверной информации из зашифрованной версии сообщения. Если кто-то посередине перехватывает это сообщение, но у него нет контрфункции, с помощью которой можно расшифровать сообщение, он не сможет прочитать его.
Алиса и Боб
Давайте проясним это с помощью тривиального примера. Предположим, что Боб хочет отправить Алисе SMS-сообщение с надписью «Я тебя люблю», но не может рисковать, если его увидит кто-то другой. (Кто-нибудь, снимающий трубку Алисы, увидит сообщение.) Чтобы успешно обмениваться зашифрованными сообщениями, Алисе и Бобу необходимо прийти к соглашению о способе шифрования / дешифрования сообщений. Давайте предположим, что это соглашение:
Каждая буква в сообщении будет заменена двузначным индексом номера последнего в английском алфавите. «A» будет «01», «B» будет «02» и т. Д. «00» будет указывать пробел. Это их функция шифрования / дешифрования, и это биективно.
| код: символ | код: символ | код: символ |
|---|---|---|
| 00: пробел | 09: я | 18: R |
| 01: A | 10: J | 19: S |
| 02: B | 11: К | 20: T |
| 03: C | 12: L | 21: U |
| 04: D | 13: М | 22: V |
| 05: E | 14: N | 23: W |
| 06: F | 15: O | 24: X |
| 07: G | 16: P | 25: Y |
| 08: H | 17: Q | 26: Z |
Поэтому Боб отправит сообщение:
09001215220500251521
Если кто-то перехватит это сообщение, оно не будет иметь для них особого смысла. Их любовь останется в секрете. Алиса, с другой стороны, сможет легко ее расшифровать и покраснеть.
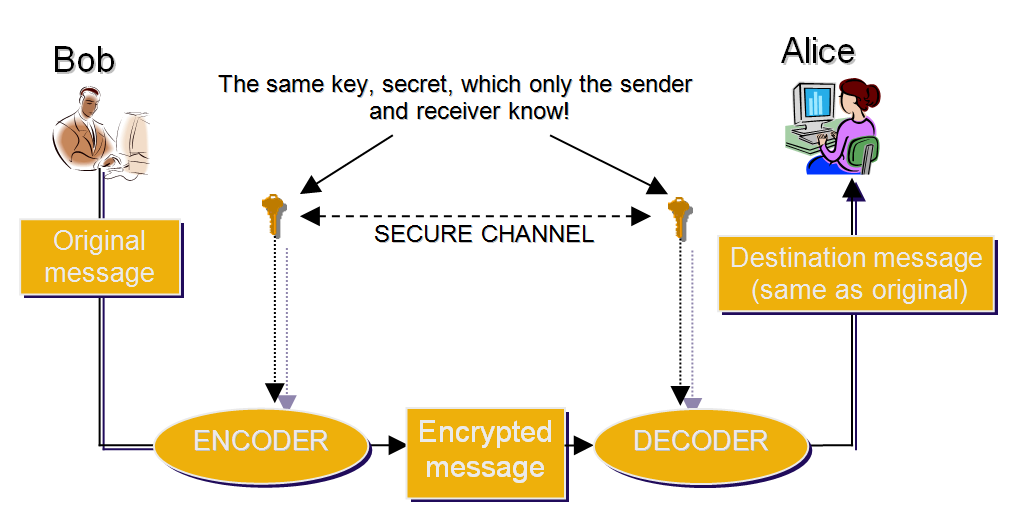
Симметричное шифрование (с закрытым ключом)
Вышеуказанный подход называется симметричным шифрованием с закрытым ключом . «Симметричный» означает, что сообщение может быть зашифровано и расшифровано с использованием одного и того же ключа (секретного). Ключ (секретный) на самом деле является функцией замены букв на цифры в буквы, которую мы описали. Это выглядит примерно так:
Такая система может показаться идеальной на первый взгляд. Конечно, более сложная биективная функция необходима, чтобы сделать это общение действительно безопасным. Система как таковая совершенно безопасна до тех пор, пока Алиса и Боб могут встретиться и заранее организовать метод шифрования / дешифрования. Но что, если, как в большинстве случаев сегодня, общающиеся люди на самом деле не находятся в непосредственной физической близости или, может быть, даже не знают друг друга? Как они могут безопасно обменять секретный ключ, не рискуя попасть в чужие руки?
Это самый большой недостаток такого шифрования с общим ключом: должен быть заранее установлен безопасный канал для обмена ключами.
Возможное решение
Понятно, что, если безопасный канал уже не существует, практически невозможно безопасно обменять секретный ключ. Если канал уже существует, тогда нет необходимости в другом.
Решение состоит не в том, чтобы найти безопасный способ обмена ключами, а в том, чтобы полностью исключить необходимость такого обмена. Это может быть достигнуто путем добавления еще одного ключа в микс. Один из них будет использоваться только для шифрования, другой для расшифровки.
Ключ шифрования может быть доступен каждому. На самом деле, он должен быть доступен каждому, потому что без него невозможно зашифровать сообщения и отправить их получателю. Этот ключ называется открытым ключом .
Другой ключ используется только для расшифровки и не должен никому отправляться. Только получатель зашифрованной информации имеет его, и мы называем его закрытым ключом .
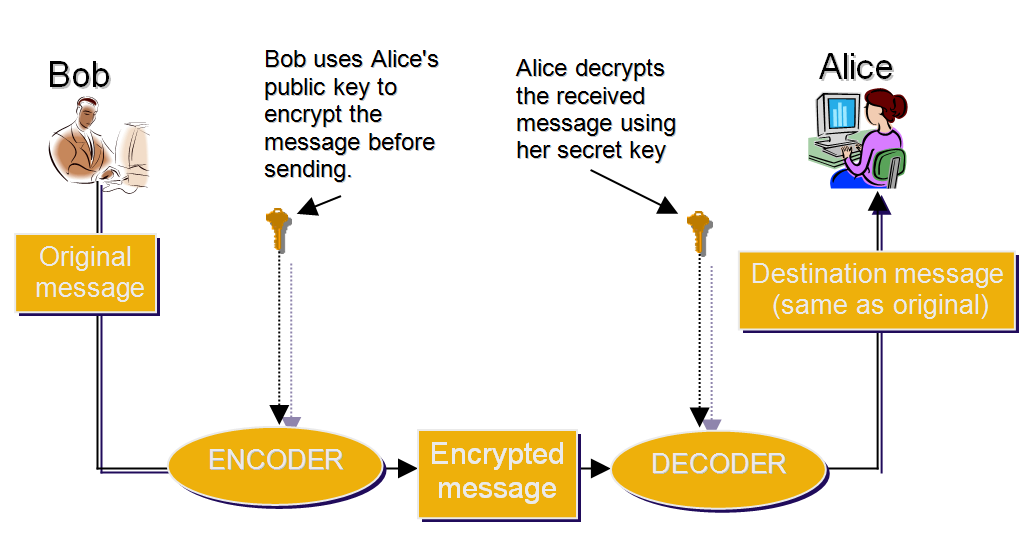
Асимметричное шифрование (с открытым ключом)
Глядя на изображение выше, мы видим, что нет необходимости в безопасном канале для обмена ключами. Асимметрия заключается в том, что невозможно зашифровать и расшифровать сообщение одним и тем же ключом. Отдельный нужен для каждого действия.
Если Боб хочет отправить Алисе зашифрованное сообщение, он должен иметь ее открытый ключ. Этот открытый ключ может быть передан ему непосредственно Алисой, или она может просто опубликовать его на своем веб-сайте, где любой, кто захочет отправить ей зашифрованное сообщение, сможет найти его. Когда Алиса получает сообщение, зашифрованное ее открытым ключом, она использует закрытый ключ для его расшифровки, что делает сообщение снова читаемым.
Если Алиса хочет отправить ответ, ей нужен открытый ключ Боба. Процедура идентична: она шифрует сообщение, отправляет его, и только Боб может расшифровать его с помощью своего закрытого ключа.
Важно отметить, что для обеспечения такого рода связи ключи должны быть сгенерированы с помощью процедур, достаточно сложных, чтобы компенсировать способность любого компьютера угадывать их в течение неоправданного времени.
Как это работает?
Если вы не до конца понимаете термины в разделе ниже, не беспокойтесь. Прочитайте их поверхностно; они будут объяснены на примере сразу после этого.
Чтобы сделать невозможным дешифрование сообщения с использованием только открытого ключа или получение секретного ключа из открытого ключа, используются однонаправленные математические функции. Однонаправленная функция такова, что f(x)x Например, если мы знаем, что сумма равна 950, мы не можем угадать, какие числа мы суммировали, чтобы получить ее, потому что число возможных комбинаций бесконечно.
Существует множество алгоритмов для вычисления таких функций. Ниже мы продемонстрируем один такой алгоритм: он называется алгоритмом RSA, основанным на инициалах имен его создателей в 1977 году (Рон Ривест, Ади Шамир, Леонард Адлеман).
-
Выберите 2 основных числа — числа, которые делятся только на 1 или на себя. Например:
- р = 61
- q = 53
-
Умножьте их
n = p x q
n = 61 x 53 = 3233 -
Вычислить наименьшее общее кратное
λ(n) (p-1) i (q-1)
nzv (p-1,q-1) = nzv (60,52) = 780Это можно сделать с помощью алгоритма, представленного здесь . -
Выберите любое число от 1 до кратного, рассчитанного ранее, чтобы это число было относительно простым или взаимно простым по отношению к начальным двум числам. Числа являются взаимно простыми, если единственное положительное число, которое разделяет их обоих, равно 1. В данном случае это
e = 17 -
Вычислить модульную мультипликативную инверсию
e(mod nzv)Мы ищемd-
(d x e) mod nzv = 1 -
(d x 17) mod 780 = 1 -
d = 413
-
-
Эти вычисления производят все необходимые компоненты набора открытого и закрытого ключей. Открытый ключ — это пара
(n, e)(n, d)Таким образом, открытый ключ(n = 3233, e = 17)Открытый ключ служит для шифрования сообщений по следующей формуле:с (м) = м 17 мод 3233
Закрытый ключ
(n=3233, d=413)Он используется для расшифровки сообщения:m (c) = c 413 mod 3233
Теперь, когда у нас есть функции шифрования и дешифрования, мы можем вернуться к нашему сценарию Алисы и Боба. Поскольку эти функции могут обрабатывать только числа, нам нужно сначала превратить буквы в числа. Таблица ASCII — стандарт, используемый компьютерами при работе с буквами в компьютерных системах — может пригодиться. Давайте сосредоточимся только на заглавных буквах здесь.
| код: символ | код: символ | код: символ |
|---|---|---|
| 32: пробел | 73: я | 82: R |
| 65: А | 74: J | 83: S |
| 66: B | 75: K | 84: Т |
| 67: C | 76: L | 85: U |
| 68: D | 77: М | 86: V |
| 69: E | 78: N | 87: W |
| 70: F | 79: O | 88: X |
| 71: G | 80: P | 89: Y |
| 72: H | 81: Q | 90: Z |
Для каждого кода ASCII из сообщения Боба нам нужно вычислить c(m) Поскольку сообщение «Я ЛЮБЛЮ ТЕБЯ», ASCII первой буквы 73. c(73)
с (м) = м 17 мод 3233
с (73) = 73 17 мод 3233
с (73) = 47477585226700098686074966922953 мод 3233
с (73) = 1486
Давайте также посчитаем остальное.
Пробел: c (32) = 32 17 mod 3233 = 1992
L: c (76) = 76 17 mod 3233 = 2726
O: c (79) = 79 17 mod 3233 = 1307
V: c (86) = 86 17 mod 3233 = 1906
E: c (69) = 69 17 mod 3233 = 28
Y: c (89) = 89 17 mod 3233 = 99
U: c (85) = 85 17 mod 3233 = 2310
Функция шифрования вычисляет mod 3233 Поэтому мы дополняем каждое число нулями с левой стороны: 1486, 1992, 2726, 1307, 1906, 0028, 1992, 0099, 1307, 2310.
Полное отправляемое сообщение:
1486199227261307190600281992009913072310
У Алисы есть свой закрытый ключ, и он может использовать его для расшифровки. Она будет использовать ранее определенную инвертированную функцию m (c) = c 413 mod 3233, где c Инвертированная функция показывает, что рассчитывается mod 3233 Таким образом, Алиса знает, что сообщение должно быть разделено на четыре набора, причем первые нули каждого из них не имеют смысла:
1486 1992 2726 1307 1906 (00)28 1992 (00)99 1307 2310
Давайте расшифруем 1486:
m (c) = c 413 mod 3233
м (1486) = 1486 413 мод 3233
m (1486) = 1,1060335282256977039647849058382e + 1310 mod 3233
м (1486) = 73
Мы получили число 73, которое согласно таблице ASCII соответствует букве «I». Следуя тому же процессу, мы можем расшифровать оставшуюся часть сообщения:
м (1992) = 1992 413 мод 3233 = 32 , ASCII 32 = размак
м (2726) = 2726 413 мод 3233 = 76 , ASCII 76 = L
m (1307) = 1307 413 mod 3233 = 79 , ASCII 79 = O
м (1906) = 1906 413 мод 3233 = 86 , ASCII 86 = V
m (28) = 28 413 mod 3233 = 69 , ASCII 69 = E
м (1992) = 1992 413 мод 3233 = 32 , ASCII 32 = размак
m (99) = 99 413 mod 3233 = 89 , ASCII 89 = Y
m (1307) = 1307 413 mod 3233 = 79 , ASCII 79 = O
m (2310) = 2310 413 mod 3233 = 85 , ASCII 85 = U
Давайте еще раз повторим, почему асимметричное шифрование лучше, чем симметричное шифрование. При симметричном шифровании есть только один ключ, который используется как для расшифровки, так и для шифрования сообщений. Если участники хотят общаться безопасно, им сначала нужно безопасно обменяться этим ключом. Если они физически удалены, это становится большой проблемой. С асимметричным шифрованием есть открытый ключ, который мы можем свободно выдавать и который люди могут использовать для шифрования сообщений, предназначенных для нас. Наш закрытый ключ остается секретным и используется только для расшифровки полученных нами сообщений. Нет необходимости в безопасном канале, по которому можно обмениваться секретным ключом, что делает асимметричное шифрование намного безопаснее, чем симметричное шифрование.
Но можно ли рассчитать закрытый ключ из открытого ключа?
Гадание частного ключа RSA
Давайте посмотрим на функции еще раз:
- Зашифровать: F (x) = x e mod (pxq)
- Расшифровать: F -1 (c) = c d мод (pxq)
Функция шифрования, то есть пара (p x q, e) Если мы знаем эту пару и хотим вычислить закрытый ключ, нам нужно найти числа pq Это означает, что мы должны факторизовать произведение pq Если мы предположим, что числа pq Чтобы факторизовать такое большое число, даже самому мощному современному суперкомпьютеру потребовалось бы абсурдное количество времени, что делало процесс математически невозможным.
Технически невозможно факторизовать число. Для этой цели разработаны специальные алгоритмы, и наиболее эффективным на данный момент является GNFS (General Number Field Sieve) . Это особенно удобно для факторизации чисел с более чем 110 цифрами. В приведенной ниже таблице указано время, необходимое для факторизации большого числа, выраженного в MIPS ( миллионах инструкций в секунду ). Соответственно, один год MIPS — это число компьютерных операций, выполняемых за один год компьютером с мощностью 1 MIPS. Это число составляет 3,1536 х 10 13 .
| Длина ключа | MIPS-годы, необходимые для его факторизации |
|---|---|
| 512-bitni | +30,000 |
| 768-bitni | 200.000.000 |
| 1024-bitni | 300.000.000.000 |
| 2048-bitni | 300.000.000.000.000.000.000 |
Если предположить, что применяемый алгоритм умножает 1024-битные числа, производя 2048-битный продукт, и что самые мощные на сегодняшний день процессоры персональных компьютеров имеют около 300 000 MIPS , это число становится довольно высоким. Даже самым мощным современным квантовым компьютерам с мощностью 100 миллионов MIPS (что является редкостью, если они вообще существуют) потребовалось бы 3 000 000 000 000 лет для факторизации 2048-разрядного числа.
Простые числа Мерсенна
Учитывая, что большие простые числа являются основной идеей алгоритма RSA, все более важно найти большие простые числа. Существует подкласс простых чисел, называемых простыми числами Мерсенна, и они выглядят так: 2 n -1. Их назвали в честь французского монаха, который первым (ошибочно) опознал 11 из них. В наши дни происходит большое движение по поиску максимально возможных простых чисел Мерсенна. (Подробную информацию можно найти на сайте Mersenne.org .) Последнее (49-е) и самое большое число Мерсенна до сих пор было найдено 7 января 2016 года. Это 2 74,207,281 -1 и 22,338,618 цифр. Тот, который был обнаружен 1 января 2013 года: это было 2 57 885 161 -1, и в нем почти на 5 миллионов меньше цифр, чем в 49-м номере.
Еще один забавный факт о простых числах: EFF, Electronic Frontier Foundation, имеет награды за большие простые числа. Их веб-сайт перечисляет эти вознаграждения и показывает, что вознаграждение в 50 000 долларов за поиск простого числа в 1 миллион и вознаграждение в 100 000 долларов за поиск простого числа в 10 миллионов было выдано с вознаграждениями в размере 150 000 и 250 000 долларов за 100 миллионов и 1 миллиард долларов. цифры соответственно еще ожидаются. Есть хорошая идея алгоритма? Может быть, вы сможете найти номер!
Асимметричное шифрование и биткойны
Так что же все это имеет отношение к криптовалюте, кроме того, что делится названием «крипто»?
Хотя приведенное ниже применимо почти ко всем криптовалютам, давайте возьмем в качестве примера самую известную — биткойны. Биткойн также использует пару открытый / закрытый ключ. Открытый ключ — или, по крайней мере, его форма — это адрес, на который вы можете отправить несколько биткойнов. Как и в зашифрованных сообщениях, где нужен открытый ключ, чтобы кто-то мог отправить нам сообщение, а с биткойнами открытый ключ нужен, чтобы кто-то мог отправить нам деньги. С другой стороны, закрытый ключ позволяет нам подтвердить, одобрить и выполнить транзакцию, с помощью которой мы отправляем некоторые из наших биткойнов с нашего адреса (аккаунта) на чей-либо открытый ключ (адрес).
Идея похожа, но у Биткойна другой подход к вычислению закрытого и открытого ключа. Закрытый ключ биткойна представляет собой 256-битное число. Как правило, мы имеем дело с большим числом, случайно выбранным из набора из 2 256 чисел. Это чуть более 10 77 возможных вариантов. Это может показаться не таким уж большим, но, учитывая оценку, что во всей вселенной насчитывается 10 80 атомов, размер этого числа может заставить нас задуматься. Простой подсчет всех этих чисел со скоростью один миллиард в секунду занял бы больше времени, чем возраст вселенной.
Таким образом, у нас есть закрытый ключ, который известен только нам и который не может быть угадан кем-либо или каким-либо компьютером в разумные сроки. В протоколе Биткойн закрытый ключ используется для вычисления открытого ключа с использованием алгоритма ECC, криптографии с эллиптической кривой . Этот алгоритм основан на кривой, функция которой может быть математически выражена как y 2 = x 3 + ax + b . Результатом является открытый ключ. Этот URL и этот URL подробно объясняют алгоритм, если вам интересно.
В Биткойне открытый ключ — это не адрес для отправки денег, но его можно легко рассчитать по следующей формуле:
address = RIPEMD160 (SHA256 (public key))
Этот URL содержит подробную информацию о процессе, если вы заинтересованы.
Вывод
Важно помнить разницу между кодированием и шифрованием. Кодирование — это процесс создания отправленного сообщения, максимально идентичного оригиналу, чтобы минимизировать ошибки. Шифрование делает сообщение нечитаемым для всех, кроме предполагаемого получателя.
Существует несколько видов шифрования, основные из которых асимметричные и симметричные. Мы рассмотрели первое в этой статье и объяснили, что в отличие от симметричного шифрования асимметричное шифрование вводит открытый и закрытый ключ, а не только один закрытый ключ, общий для сторон, что делает возможным безопасную связь по незащищенным каналам.
Преимущество асимметричного шифрования становится очевидным в криптовалюте, где открытый ключ используется для получения средств и проверки баланса и транзакций, тогда как закрытый ключ является единственным способом фактически подписывать сообщения и отправлять токены.