Вы когда-нибудь сталкивались с шумным изображением? Я имею в виду изображение, которое было не очень четким при просмотре? Я думаю, что мы очень часто сталкиваемся с такими изображениями, особенно когда многие изображения в настоящее время делаются нашими камерами мобильных телефонов или цифровыми камерами низкого разрешения.
Если бы у вас было только то шумное изображение, которое что-то для вас значит, но проблема в том, что его нельзя просмотреть должным образом, будет ли решение для восстановления после такого шума?
Это где фильтрация изображений вступает в игру, и это то, что я буду описывать в этом уроке. Давайте начнем!
Фильтрация изображений
Фильтрация изображений — популярный инструмент, используемый при обработке изображений. В конце концов, мы используем фильтрацию изображений, чтобы удалить шум и любые нежелательные функции из изображения, создавая лучшую и улучшенную версию этого изображения. Существуют два типа фильтров: линейный и нелинейный . Примерами линейных фильтров являются средние и лапласовские фильтры. Нелинейные фильтры представляют собой фильтры, такие как медиана, минимум, максимум и фильтры Собеля.
Каждый из этих фильтров имеет определенное назначение и предназначен для удаления шума или улучшения некоторых аспектов изображения. Но как осуществляется фильтрация? Это то, что мы увидим в следующем разделе.
Как мы выполняем фильтрацию изображения?
Чтобы выполнить процесс фильтрации изображений, нам нужен фильтр , также называемый маской . Этот фильтр обычно представляет собой двумерное квадратное окно, то есть окно с равными размерами (шириной и высотой).
Фильтр будет включать числа. Эти числа называются коэффициентами , и именно они фактически определяют эффект фильтра и то, как будет выглядеть выходное изображение. На рисунке ниже показан пример фильтра 3x3 , имеющего девять значений (коэффициентов).
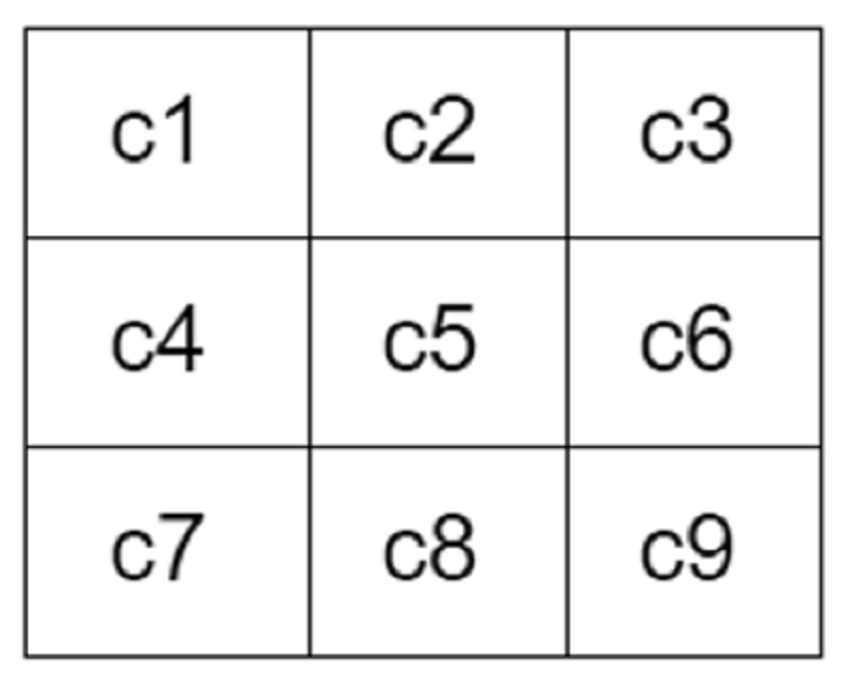
Чтобы применить фильтр, окно 3x3 скользит по изображению. Этот процесс скольжения окна фильтра по изображению называется сверткой в пространственной области . Окно будет размещено на каждом пикселе (т. Е. Думать о нем как о ячейке в матрице) на изображении, где центр фильтра должен перекрывать этот пиксель.
Как только это перекрытие произойдет, пиксели в подизображении, над которым находится фильтр, будут умножены на соответствующие коэффициенты фильтра. В этом случае у нас будет новая матрица с новыми значениями, похожими на размер фильтра (т.е. 3x3 ). Наконец, значение центрального пикселя будет заменено новым значением с использованием конкретного математического уравнения в зависимости от типа используемого фильтра (то есть медианного фильтра).
Я знаю, что вышеупомянутый параграф немного многословен. Давайте рассмотрим пример того, как фильтр изображений применяется в действии. Предположим, у нас есть следующее подизображение, где наш фильтр перекрывается ( i и j относятся к расположению пикселя в подизображении, а I относится к изображению):
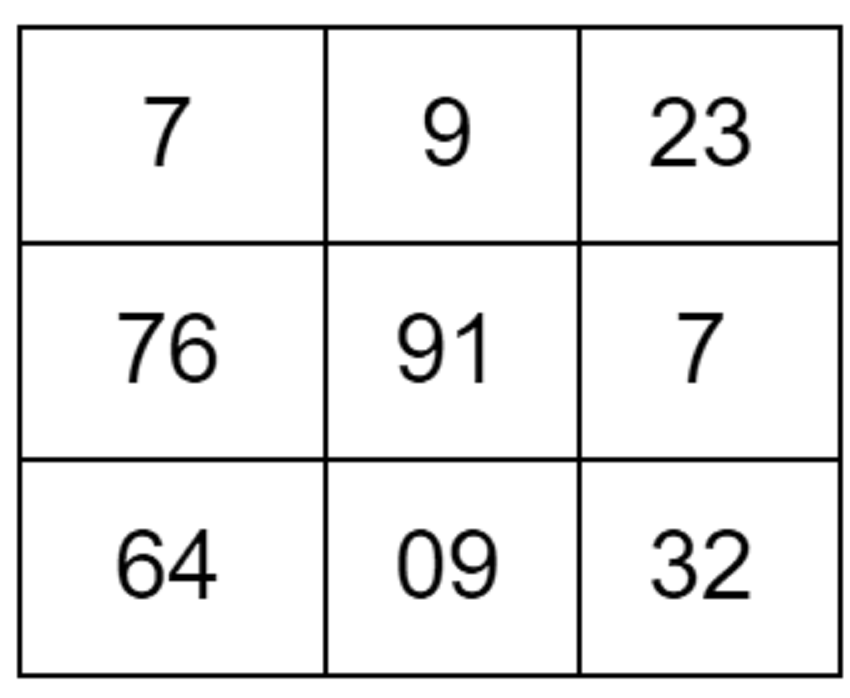
Свертка нашего фильтра, показанного на первом рисунке с изображением выше, будет выглядеть, как показано ниже, где I_new(i,j) представляет результат в местоположении (i,j) .
|
1
2
3
|
I_new(i,j) = v1 x I(i-1,j-1) + v2 x I(i-1,j) + v3 x I(i-1,j+1) +
v4 x I(i,j-1) + v5 x I(i,j) + v6 x I(i,j+1) + v7 x I(i+1,j-1) +
v8 x I(i+1,j) + v9 x I(i+1,j+1)
|
Процесс повторяется для каждого пикселя в изображении, включая пиксели на границе изображения. Но, как вы можете догадаться, при установке фильтра на граничных пикселях часть фильтра будет находиться за пределами изображения. В этом случае мы выполняем заполнение .
Этот процесс просто означает, что мы вставляем новые значения пикселей в подизображение под частью фильтра, которая выходит за пределы изображения перед процессом свертки, поскольку эта часть, очевидно, не содержит никаких значений пикселей. Это за пределами изображения! Эти дополненные пиксели могут быть нулями или постоянным значением. Существуют и другие методы установки значений отступов, но они выходят за рамки этого руководства.
Я думаю, что на данный момент достаточно теории, так что давайте пойдем и запачкаем руки программированием! В этом уроке я расскажу о медианном фильтре (то есть нелинейном) и среднем фильтре (то есть линейном) и о том, как мы можем реализовать их в Python.
Медианный фильтр
В медианном фильтре мы выбираем скользящее окно, которое будет перемещаться по всем пикселям изображения. Здесь мы собираем значения пикселов, которые попадают под фильтр, и принимаем медиану этих значений. Результат будет присвоен центральному пикселю.
Скажем, наш фильтр 3x3 имел следующие значения после размещения его на фрагмент изображения:
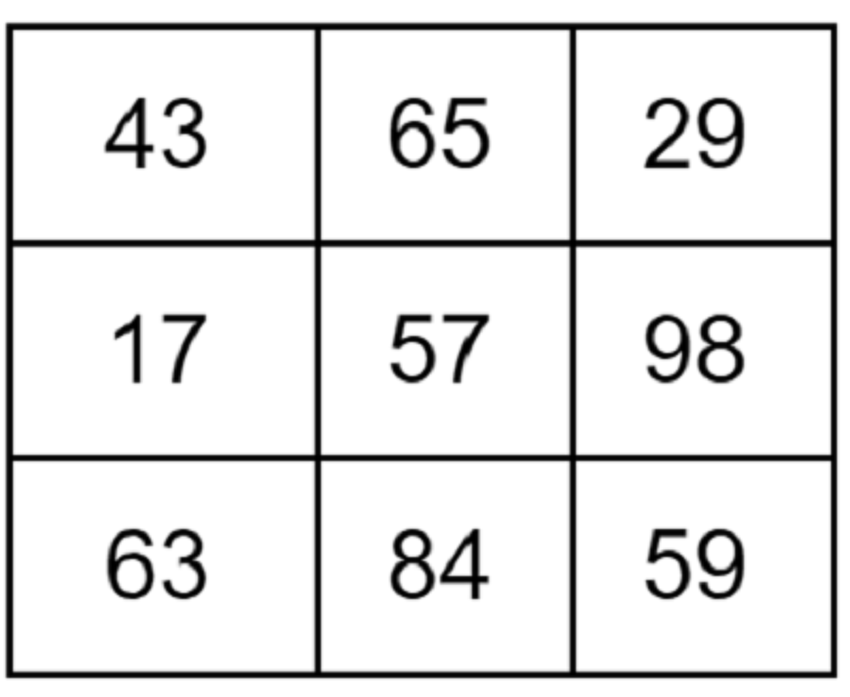
Посмотрим, как рассчитать медиану. Медиана, по своей сути, является средним числом отсортированного списка чисел. Таким образом, чтобы найти медиану для указанного выше фильтра, мы просто сортируем числа по убыванию, и середина этих чисел будет нашим медианным значением. Сортировка значений в нашем окне 3x3 даст нам следующее:
|
1
|
17 29 43 57 59 63 65 84 98
|
Чтобы найти среднее число (медиану), мы просто посчитаем количество имеющихся у нас значений, добавим 1 к этому числу и разделим на 2. Это даст нам местоположение среднего значения в окне, которое является нашим медианным значением. Таким образом, медиана будет в местоположении 9+1/2 = 5 , что составляет 59 . Это значение будет новым значением пикселя под центром нашего окна 3x3 .
Этот тип фильтра используется для удаления шума и лучше всего работает с изображениями, которые страдают от шума соли и перца . На изображении ниже показан пример изображения, страдающего от такого шума:

Теперь давайте напишем скрипт Python, который будет применять медианный фильтр к изображению выше. Для этого примера мы будем использовать библиотеку OpenCV. Пожалуйста, проверьте Установить OpenCV-Python в Windows и Установите OpenCV 3.0 и Python 2.7+ в Ubuntu для установки OpenCV.
Чтобы применить медианный фильтр, мы просто используем cv2.medianBlur() . Наш скрипт может выглядеть следующим образом:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
|
import cv2
import argparse
# create the argument parser and parse the arguments
ap = argparse.ArgumentParser()
ap.add_argument(‘-i’, ‘—image’, required = True, help = ‘Path to the input image’)
args = vars(ap.parse_args())
# read the image
image = cv2.imread(args[‘image’])
# apply the 3×3 median filter on the image
processed_image = cv2.medianBlur(image, 3)
# display image
cv2.imshow(‘Median Filter Processing’, processed_image)
# save image to disk
cv2.imwrite(‘processed_image.png’, processed_image)
# pause the execution of the script until a key on the keyboard is pressed
cv2.waitKey(0)
|
Обратите внимание, что я использовал argparse , так как это хорошая практика, чтобы проявлять гибкость и использовать командную строку для передачи изображения, к которому мы хотим применить медианный фильтр, в качестве аргумента нашей программы.
После передачи нашего изображения в качестве аргумента командной строки, мы читаем это изображение с помощью функции cv2.imread() . Затем мы применяем медианный фильтр, используя medianBlur() , передавая наше изображение и размер фильтра в качестве параметров. Изображение отображается с помощью функции cv2.imshow() и сохраняется на диск с помощью cv2.imwrite() .
Результат приведенного выше сценария выглядит следующим образом:

Ну, что вы думаете? Очень красивый — красивый и чистый образ без шума.
Вы можете скачать приведенный выше код из моего хранилища медианного фильтра на GitHub.
Средний фильтр
Средний фильтр является примером линейного фильтра. Он в основном заменяет каждый пиксель в выходном изображении на среднее (среднее) значение окрестности. Это приводит к сглаживанию изображения (уменьшению количества вариаций интенсивности между пикселем и следующим), удалению шума с изображения и повышению яркости изображения.
Таким образом, при средней фильтрации каждый пиксель изображения будет заменен средним значением его соседей, включая сам пиксель. Ядро 3x3 используемое для средней фильтрации, показано на рисунке ниже, хотя можно использовать и другие размеры ядра (например, 5×5):
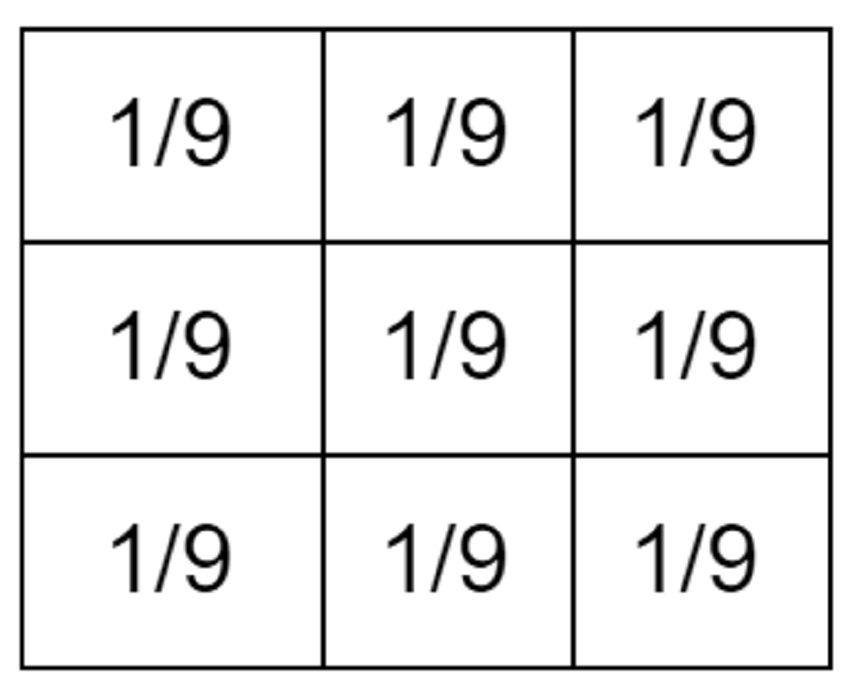
То, что вышеописанное ядро на самом деле пытается нам сказать, это то, что мы суммируем все элементы под ядром и берем среднее (среднее) от суммы.
Здесь важно упомянуть, что все элементы среднего ядра должны:
- сумма до 1
- быть таким же
Давайте рассмотрим пример, чтобы прояснить ситуацию. Скажем, у нас есть следующее изображение:
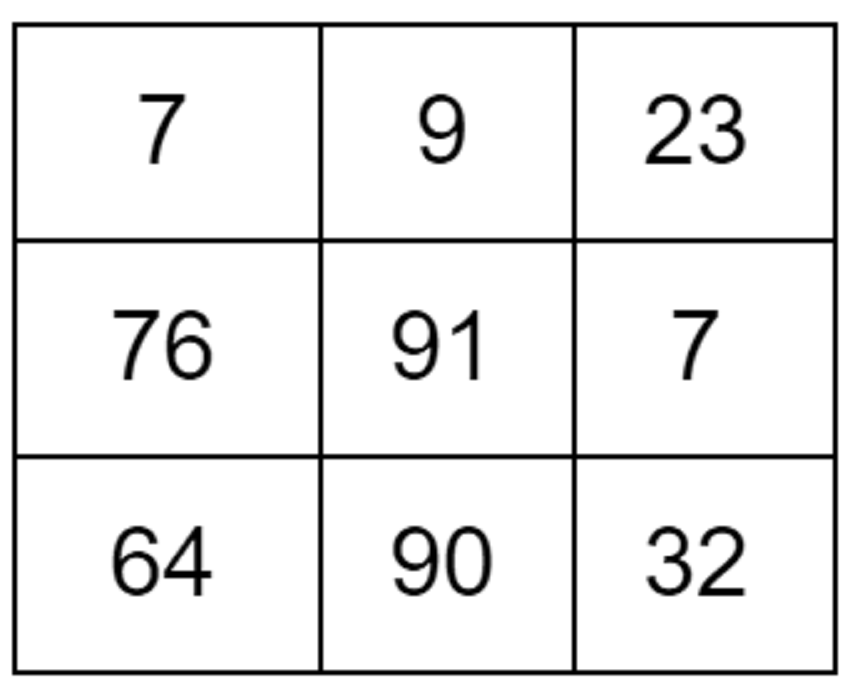
При применении фильтра средних значений мы будем делать следующее:
|
1
|
(7+9+23+76+91+7+64+90+32)/9 = 44
|
Точный результат — 44.3 , но я округлил результат до 44 . Таким образом, новое значение для центрального пикселя — 44 вместо 91 .
Теперь к части кодирования. Допустим, у нас есть следующее шумное изображение:

На этом этапе мы хотим применить фильтр средних значений к изображению выше и увидеть результаты применения такого фильтра.
Код для выполнения этой операции выглядит следующим образом:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
|
import cv2
import numpy as np
import argparse
# create the argument parser and parse the arguments
ap = argparse.ArgumentParser()
ap.add_argument(‘-i’, ‘—image’, required = True, help = ‘Path to the input image’)
args = vars(ap.parse_args())
# read the image
image = cv2.imread(args[‘image’])
# apply the 3×3 mean filter on the image
kernel = np.ones((3,3),np.float32)/9
processed_image = cv2.filter2D(image,-1,kernel)
# display image
cv2.imshow(‘Mean Filter Processing’, processed_image)
# save image to disk
cv2.imwrite(‘processed_image.png’, processed_image)
# pause the execution of the script until a key on the keyboard is pressed
cv2.waitKey(0)
|
Из кода обратите внимание, что мы использовали ядро 3x3 для нашего среднего фильтра. Мы также использовали filter2D() для применения среднего фильтра. Первый параметр этой функции — наше входное изображение, второй — желаемая глубина ddepth выходного изображения, а третий параметр — наше ядро. Присвоение -1 для параметра ddepth означает, что выходное изображение будет иметь ту же глубину, что и входное изображение.
После запуска кода на нашем шумном изображении, это был результат, который я получил:

Если вы наблюдаете выходное изображение, мы видим, что оно более плавное, чем изображение с шумом. Миссия выполнена!
Вы можете скачать приведенный выше код из моего среднего хранилища фильтров на GitHub.
Вывод
Как мы видели в этом руководстве, Python позволяет нам выполнять сложные задачи, такие как фильтрация изображений, особенно с помощью библиотеки OpenCV, простым способом.
Кроме того, не стесняйтесь посмотреть, что у нас есть в наличии для продажи и для изучения на рынке , и не стесняйтесь задавать любые вопросы и предоставлять ценные отзывы, используя канал ниже.