Статьи

Еще один способ научиться рекурсии

Декабрь 16, 2018

Каждый семестр я провожу опрос, чтобы получить отзывы о моем преподавании. В прошлом семестре кто-то наконец дал мне идею для новой статьи. В частности, они хотели узнать больше о рекурсии, поэтому я решил собрать несколько советов.

Обзор рекурсии

Для тех из вас, кто впервые изучает рекурсию, я решил дать краткий обзор этой концепции.

В частности, рекурсия — это метод решения проблем, основанный на решении небольших подзадач. Другими словами, вместо непосредственного решения проблемы мы продолжаем разбирать проблему до тех пор, пока не доберемся до более мелкой проблемы, которую мы можем реально решить. Затем мы используем ответ на наименьшую подзадачу, чтобы двигаться назад, пока у нас не будет ответа на наш первоначальный вопрос.

Например, допустим, мы хотим вычислить 2 6 . Обычно мы разбили бы это на повторное умножение. Другими словами, мы взяли бы 2 и умножили бы это на себя 6 раз, чтобы получить 64. В Информатике мы называем эту итерацию метода решения проблем, и мы обычно видим это в форме цикла:

1
2
3
4
5
6
7
def iterative_power(base, exponent):
  product = 1
  for i in range(exponent):
    product *= base
  return product
 
print(iterative_power(2, 6))

Конечно, что если мы уже знали ответ на какую-то меньшую подзадачу. Например, что если бы мы знали, что 2 5 — это 32? Затем мы могли бы напрямую вычислить 2 6 , умножив 2 5 на 2. Вот идея рекурсии:

1
2
3
4
5
def recursive_power(base, exponent):
  if exponent == 0:
    return 1
  else:
    return recursive_power(base, exponent - 1) * base

В этой статье мы рассмотрим другой способ мышления рекурсии. Надеюсь, это поможет вам понять концепцию лучше, чем раньше.

Почему рекурсия так сложна?

Хотя функциональное программирование в настоящее время возвращается, оно не оказало большого влияния на то, как мы учимся кодировать. В результате, большинство людей начинают писать с C-подобного императивного языка программирования. Например, я начал работать с Java и перешел на такие языки, как C, C ++, C # и Python.

К сожалению, недостатком изучения языков, таких как C, является то, что мы ограничены в том, как мы думаем о решении проблем. Другими словами, набор инструментов, который предоставляется нам на этих языках, в значительной степени смещен в сторону ветвления (т. Е. Операторов и циклов).

В результате, интуиция за рекурсией не встроена с самого начала. Вместо этого мы вынуждены вводить рекурсию с использованием надуманных примеров, которые связаны с итеративными решениями. В противном случае, как еще мы будем связаны.

Кроме того, императивные языки, такие как C, требуют много накладных расходов, прежде чем вводить рекурсию. Например, вам, вероятно, пришлось выучить такие понятия, как переменные, ветвления и функции, прежде чем вы могли даже подумать о рекурсии. На самом деле, я не был лично знаком с этой концепцией до моего первого курса по структурам данных.

В целом, может быть трудно понять рекурсию, потому что это требует, чтобы ваше понимание кодирования перевернулось с ног на голову. К счастью, есть способы разорвать цикл (каламбур абсолютно предназначен).

Изучение рекурсии через дизайн по контракту

Недавно я готовился преподавать курс по программным компонентам в Университете штата Огайо, и одной из тем, которые они освещали в этом курсе, была рекурсия. Конечно, в то время я уже был хорошо знаком с рекурсией, но я думал, что способ преподавания предмета был действительно элегантным. В результате я решил, что смогу передать вам этот метод. Тем не менее, нам нужно сначала заняться дизайном по контракту.

Введение в дизайн по контракту

Я прошу прощения, если я немного повторюсь, поскольку в прошлом немного писал о Design by Contract — главным образом в связи с тестированием JUnit . Естественно, я думаю, что сейчас я немного лучше пишу, но не стесняйтесь ссылаться и на эту статью.

В любом случае, Design by Contract (DbC) — это философия программирования, в которой мы думаем о функциях с точки зрения контрактов. Другими словами, мы хотим предоставить какую-то гарантию нашим пользователям, когда они используют одну из наших функций. В частности, мы просим наших пользователей выполнять каждую функцию при определенных условиях (или предварительных условиях). Как следствие, мы обещаем, что каждая функция будет вести себя определенным образом (так называемые постусловия).

DbC важен в рекурсии, потому что он позволяет нам точно указать, что функция будет делать при определенных условиях. Например, степенные функции, которые мы определили ранее, работают только до тех пор, пока мы указываем несколько предварительных условий:

  • Оба параметра должны быть целыми числами (можно позаботиться о некоторых подсказках типов)
  • Параметр power не может быть отрицательным

В результате мы обещаем, что обе функции вернут base поднятую до некоторой power . Если пользователь вводит неверные данные, мы не даем никаких обещаний, поскольку они явно нарушили договор. Конечно, мы всегда можем предоставить некоторую проверку ввода, чтобы предотвратить неприятные ошибки, но это выходит за рамки DbC.

Бесплатный обед для всех

В OSU мы вводим рекурсию, полностью игнорируя идею рекурсии. Вместо этого мы используем то, что мы знаем о Проектировании по Контракту, чтобы начать неявную реализацию рекурсивных функций.

Например, давайте еще раз посмотрим на эту функцию мощности, о которой мы продолжаем говорить:

1
2
3
4
5
6
7
def power(base: int, exponent: int) -> int:
  """Computes the base ^ exponent.
 
  Precondition: exponent >= 0
  Postcondition: base ^ exponent
  """
  return FreeLunch.power(base, exponent)

В этом примере мы представляем новую мощную функцию из волшебной библиотеки под названием FreeLunch . Насколько нам известно, эта новая функция мощности точно такая же, как та, которую мы написали, — точно такой же контракт.

Теперь, ради аргумента, допустим, что у этой FreeLunch мощности FreeLunch есть требование: ее вход должен быть «меньше», чем вход нашей функции мощности. Что мы можем сделать, чтобы это работало?

Что ж, если мы уменьшим показатель степени, мы можем добавить его обратно, умножив основание (то есть x 5 = x 4 * x). Давайте попробуем это:

1
2
3
4
5
6
7
def power(base: int, exponent: int) -> int:
  """Computes the base ^ exponent.
 
  Precondition: exponent >= 0
  Postcondition: base ^ exponent
  """
  return FreeLunch.power(base, exponent - 1) * base

На этом этапе, как мы можем проверить, что это работает? Что ж, давайте попробуем некоторые материалы. Например, мы могли бы попробовать 2 6 снова. Если мы проследим за кодом, мы заметим, что мы вызываем FreeLunch.power(2, 5) который является полностью допустимым вводом. Другими словами, мы получим 32 обратно, которые мы умножаем на 2, чтобы получить 64, правильный ответ.

Тем не менее, есть ли входные данные, которые потерпят неудачу? Абсолютно! Поскольку FreeLunch мощности FreeLunch имеет тот же контракт, что и наша функция мощности, существуют недействительные входные данные. Например, нам следует избегать любой ситуации, когда FreeLunch мощности FreeLunch передается значение меньше 0:

01
02
03
04
05
06
07
08
09
10
def power(base: int, exponent: int) -> int:
  """Computes the base ^ exponent.
 
  Precondition: exponent >= 0
  Postcondition: base ^ exponent
  """
  if exponent == 0:
    return 1
  else:
    return FreeLunch.power(base, exponent - 1) * base

Теперь мы можем быть уверены, что наша силовая функция работает.

Там нет бесплатного обеда

Как вы, вероятно, можете себе представить, реализация функции power таким запутанным способом была всего лишь упражнением, чтобы заставить вас использовать рекурсию. Другими словами, мы можем полностью удалить класс FreeLunch выше, и у нас будет полностью функционирующее рекурсивное решение:

01
02
03
04
05
06
07
08
09
10
def power(base: int, exponent: int) -> int:
  """Computes the base ^ exponent.
 
  Precondition: exponent >= 0
  Postcondition: base ^ exponent
  """
  if exponent == 0:
    return 1
  else:
    return power(base, exponent - 1) * base

Теперь возникает вопрос: зачем нам все эти усилия вводить рекурсию? В конце концов, почти в каждом другом руководстве по рекурсии используется какой-то стек. Почему бы нам не сделать это?

Хотя учить рекурсию с использованием стека совершенно справедливо, для студентов это бывает довольно обременительно. Например, представьте трассировку через функцию питания, описанную выше, без использования нашего трюка с FreeLunch. Если мы предоставим два случайных входа — скажем, основание 2 и показатель степени 6 — нам придется прослеживать каждый вызов функции степени, пока мы не достигнем наименьшей подзадачи. На бумаге это шесть следов для одного простого примера!

При таком обучении ученики часто теряются в рекурсии, когда они пробуют различные материалы в своей программе. Если бы они вместо этого приостановили свое неверие и доверие к контракту, они могли бы доказать свою функциональную работу за один проход. Конечно, им нужно будет обратить внимание на их входные данные ( см. Математическую индукцию ).

Рекурсивные корни

Теперь, когда мы увидели несколько примеров, я хочу немного рассказать о том, откуда взялась рекурсия. В конце концов, рекурсия часто является этим страшным предметом, который, кажется, появляется, когда удобно в лекциях по информатике. К счастью, у него гораздо более интересная история, чем эта.

Помните, как мы смотрели на степенную функцию ранее? Это было не случайно. На самом деле, существует множество математических формул, которые можно записать рекурсивно. Например, формула мощности выглядит следующим образом:

a n = a n-1 * a (если n> 0)

Естественно, a n может непрерывно разлагаться до тех пор, пока показатель степени не станет равным 1 или 0, в зависимости от того, как мы хотим завершить нашу рекурсию. В наших примерах выше мы игнорировали, когда n = 1, потому что n = 0 дает нам 1, который работает нормально. Другими словами, добавление дополнительного регистра для n = 1 не влияет на результат.

Как и власть, есть несколько других рекурсивных формул, которые вы, вероятно, уже знаете. Например, последовательность Фибоначчи определяется рекурсивной формулой:

a n = a n-1 + a n-2

Чтобы убедиться, что эта формула работает, мы должны определить первые два термина. Затем все работает отлично. В зависимости от того, кого вы спрашиваете, первые два условия могут быть 0 и 1 или 1 и 1. Независимо от того, обе пары чисел работают.

Если мы хотим затем вычислить любой произвольный член в последовательности, мы разлагаем исходную функцию до тех пор, пока не достигнем ни одного из наших базовых случаев. Например, следующая диаграмма иллюстрирует, как мы вычислим пятый член в последовательности Фибоначчи:

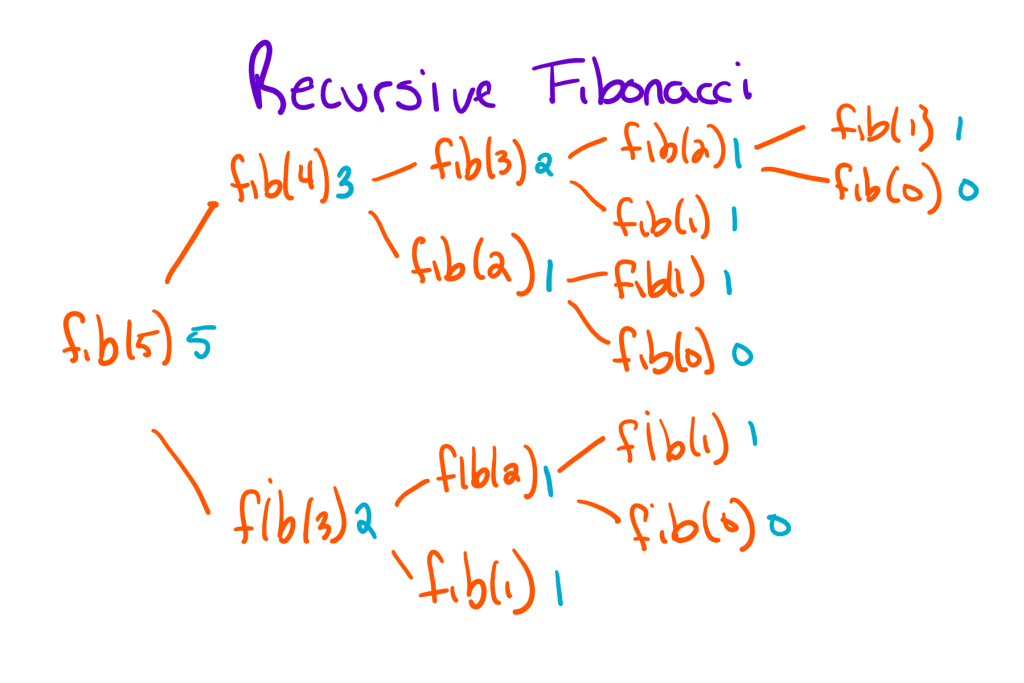
Мы можем спорить об эффективности рекурсивного алгоритма, подобного этому, весь день, но это верный способ решения проблемы. Вместо того, чтобы решать проблему поэтапно, мы разбиваем ее на более мелкие, пока не найдем проблему, которую можем решить. Затем мы используем этот результат, чтобы вернуться назад, пока не получим наш окончательный ответ.

Рекурсивные структуры

Теперь, когда мы рассмотрели рекурсию через призму математики и дизайна по контракту, возникает вопрос: как мы распознаем проблемы, в которых рекурсия была бы полезной? Другими словами, есть ли проблемы, которые имеют рекурсивную структуру? Давайте поговорим об этом.

Оказывается, вокруг нас есть рекурсивные структуры. Например, последовательность Фибоначчи явно определяется как рекурсивная формула. Конечно, есть и другие типы рекурсивных структур. Например, вышеприведенная древовидная диаграмма является рекурсивной структурой. В конце концов, каждый вызов «fib» создает еще одно дерево. Другими словами, внутри деревьев есть деревья.

Помимо технологий, существуют и другие примеры рекурсивных структур, таких как фракталы, которые представляют собой наборы геометрических фигур, сохраняющих свою структуру в любом масштабе. Для тех из вас, кто знаком с Triforce , это идеальный пример простого фрактала: треугольник из треугольников.

Аналогично, существует несколько повседневных рекурсивных структур, таких как каталоги (папки, содержащие папки) и лук (лук, содержащий лук). Другими словами, иерархические и вложенные структуры обычно являются хорошими показателями рекурсии.

Из этих примеров можно ли распознать какие-либо шаблоны? Да, конечно! Ключевым моментом здесь является наблюдение за структурой проблемы. Сама проблема состоит из подобных проблем? Если это так, рекурсия, вероятно, путь. Если нет, возможно, имеет смысл попробовать что-то еще.

Знаменитые рекурсивные алгоритмы

Учитывая все вышесказанное, я думаю, что полезно составить короткий список известных рекурсивных алгоритмов для вдохновляющих целей. Не стесняйтесь поделиться некоторыми из ваших любимых в комментариях:

И с этим, я думаю, что мы покрыли все. Если у вас есть какие-либо вопросы, которые не были рассмотрены в статье, не стесняйтесь направлять их в комментарии ниже.

Посмотреть рекурсию

Если вы хотите узнать больше о рекурсии, я рекомендую проверить эту действительно замечательную статью под названием « Ещё один способ узнать рекурсию» (извините, мне пришлось сделать хотя бы одну шутку с рекурсией). В противном случае, спасибо, что заглянули!

Если вы хотите остаться, у меня есть много других статей для вас:

Еще раз спасибо за вашу поддержку. Каждый маленький кусочек проходит долгий путь!

Смотрите оригинальную статью здесь: еще один способ научиться рекурсии

Мнения, высказанные участниками Java Code Geeks, являются их собственными.

38
Share: