TL; DR: я сделал компьютерную симуляцию эволюции поведения обезьян, продолжаю читать, чтобы увидеть, как проблема была изначально сформулирована в «Эгоистичном гене» . Первая часть показывает мою реализацию Java , вторая часть отображает результаты и выводы.
Эта проблема
Недавно я прочитал книгу «Эгоистичный ген » Ричарда Докинза , очень широкую книгу, несмотря на то, что мне 40 лет. Хотя первоначальный текст иногда устарел (« вы могли бы упаковать в череп всего несколько сотен транзисторов — больше, как триллионы в наши дни , закон Мура» ), общие утверждения так же привлекательны, как и раньше.
Одна из глав, которая особенно привлекла мое внимание, как компьютерного инженера, была о животных, выполняющих социальную груминг , как некоторые виды обезьян (см. Рисунок выше). Позвольте мне процитировать соответствующую главу :
Предположим, что вид […] паразитируется особенно неприятным видом клеща, который несет опасное заболевание. Очень важно, чтобы эти клещи были удалены как можно скорее. […] Человек может быть не в состоянии достичь своей собственной головы, но нет ничего проще, чем для друга сделать это для него. Позже, когда друг сам паразитирует, доброе дело может быть окуплено. […] Это имеет непосредственный интуитивный смысл. Любой, обладающий сознательным предвидением, может понять, что разумно вступать во взаимные договоренности по поводу возвращения к царапинам. […]
Предположим, у B есть паразит на макушке. А тянет его от себя. Позже приходит время, когда у А на голове паразит. Естественно, он ищет В, чтобы В мог вернуть свой добрый поступок. Б просто поворачивает нос и уходит. Б — это обман, человек, который принимает пользу от альтруизма других людей, но который не окупает его или который платит недостаточно. Читы работают лучше, чем беспорядочные альтруисты, потому что они получают выгоды, не оплачивая расходы. Безусловно, стоимость ухода за головой другого человека кажется небольшой по сравнению с выгодой удаления опасного паразита, но она не является незначительной. Немного ценной энергии и времени нужно потратить.
Пусть население состоит из людей, которые принимают одну из двух стратегий. […] Назовите две стратегии Sucker и Cheat. Присоски ухаживают за всеми, кто в этом нуждается, без разбора. Читы принимают альтруизм от лохов, но они никогда не ухаживают за кем-либо еще, даже за кого-то, кто их ранее готовил. […] Читы будут лучше, чем лохи. Даже если все население склоняется к вымиранию, никогда не будет времени, когда лохи будут лучше, чем читы. Поэтому, пока мы рассматриваем только эти две стратегии, ничто не может остановить вымирание лохов и, весьма вероятно, вымирание всего населения.
Но теперь, предположим, есть третья стратегия, называемая Grudger. Grudgers ухаживают за незнакомцами и людьми, которые ранее ухаживали за ними. Однако, если кто-то обманывает их, они запоминают инцидент и обижаются: они отказываются ухаживать за этим человеком в будущем. В популяции недоброжелателей и лохов невозможно сказать, что есть что. Оба типа ведут себя альтруистически по отношению ко всем остальным […]. Если по сравнению с читами хруджеры редки, то ген вырубится. Однако, как только злоумышленникам удастся нарастить численность, чтобы они достигли критической пропорции, их шансы встретиться друг с другом становятся достаточно большими, чтобы компенсировать их напрасные усилия по подготовке читов. Когда эта критическая пропорция будет достигнута, они начнут получать в среднем более высокую отдачу, чем читы, и читы будут двигаться с ускоряющейся скоростью к исчезновению. […]
Цитата: Эгоистичный ген Ричарда Докинза , ISBN 0-19-857519-X.
Позже автор проводит серию компьютерных симуляций, чтобы наблюдать, как эти три стратегии играют вместе в различных условиях. Очевидно, что исходный код недоступен, и я на самом деле рад этому. Во-первых, потому что у меня была возможность написать код для удовольствия. Во-вторых: книга была опубликована в 1976 году, спустя 4 года после изобретения C и за много лет до C ++ (чтобы представить вас в перспективе), и я не совсем в настроении (я полагаю) Fortran .
Реализация
Поэтому я взломал несколько классов, чтобы провести симуляцию мошенников, лохов и недовольных по всему населению. Я хочу увидеть, как различные типы поведения влияют на численность населения. Какое поведение является стабильным и гарантирует выживание. Наконец, как смягчают случайные мутации и смерти. Я решил поэкспериментировать с некоторыми методами, а именно:
- Ручная инъекция зависимостей, без контейнера вообще
- Полностью однопоточный
- Логические часы, которые выдвинуты явно для имитации времени
Мы собираемся смоделировать популяцию обезьян (от нескольких до миллионов), каждая с независимым поведением, случайным временем жизни и так далее. Кажется очевидным использование мультиагентных решений, таких как актеры или хотя бы потоки. Однако курс « Принципы реактивного программирования» научил меня, что это часто чрезмерная инженерия. По сути, такая симуляция представляет собой последовательность событий, которые должны произойти в будущем: обезьяна должна родиться через 2 года, размножиться через 5 лет и умереть через 10. Конечно, есть еще много таких событий и больше обезьян. Однако достаточно выбросить все эти события в одну очередь с приоритетами, где ближайшие события будут первыми. Вот как Planner по сути реализован:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
public abstract class Action implements Comparable<Action> { private final Instant schedule; public Action(Clock simulationTime, Duration delay) { this.schedule = simulationTime.instant().plus(delay); } @Override public int compareTo(Action other) { return this.schedule.compareTo(other.schedule); } public abstract void run(); } //... public class Planner implements Runnable { private final Queue<Action> pending = new PriorityQueue<>(); private final SimulationClock simulationClock; public void schedule(Action action) { pending.add(action); } @Override public void run() { while (!pending.isEmpty()) { Action nearestAction = pending.poll(); simulationClock.advanceTo(nearestAction.getSchedule()); nearestAction.run(); } }} |
У нас есть Action с предопределенным schedule ( когда оно должно быть выполнено) и pending очередь будущих действий. Не нужно ждать, мы просто выбираем ближайшее действие из будущего и опережаем время симуляции:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
|
import java.time.Clock; public class SimulationClock extends Clock { private Instant simulationNow = Instant.now(); @Override public Instant instant() { return simulationNow; } public void advanceTo(Instant instant) { simulationNow = instant; } } |
Таким образом, мы по существу реализовали цикл событий, где события могут быть добавлены в любом месте в очереди (не обязательно в конце). Теперь, когда у нас есть базовая структура, давайте реализуем поведение обезьян:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
public class Sucker extends Monkey { //... @Override public boolean acceptsToGroom(Monkey monkey) { return true; } } public class Cheater extends Monkey { private final double acceptProbability; //... @Override public boolean acceptsToGroom(Monkey monkey) { return Math.random() < acceptProbability; }} public class Grudger extends Monkey { private final Set<Monkey> cheaters = new HashSet<>(); @Override public boolean acceptsToGroom(Monkey monkey) { return !cheaters.contains(monkey); } @Override public void monkeyRejectedToGroomMe(Monkey monkey) { cheaters.add(monkey); } } |
Как вы можете видеть, эти три класса фиксируют три различных поведения. Sucker всегда принимают запросы на груминг, Cheater только иногда (в оригинальной симуляции — никогда, но я сделал это настраиваемым), вспоминают Grudger которые ранее отклоняли их запрос. Обезьяны собраны в пределах класса Population , вот небольшой фрагмент:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
public class Population { private final Set<Monkey> monkeys = new HashSet<>(); private final MonkeyFactory monkeyFactory; private Population addMonkey(Monkey child) { if (!full()) { newMonkey(child); } return this; } private boolean full() { return monkeys.size() >= environment.getMaxPopulationSize(); } private void newMonkey(Monkey child) { monkeys.add(child); planner.scheduleMonkeyLifecycle(child, this); log.debug("New monkey in population {}total {}", child, monkeys.size()); } //...} |
Для каждой новой обезьяны мы планируем ее так называемый жизненный цикл, то есть события, связанные с разведением, уходом и смертью (в Planner ):
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
void scheduleMonkeyLifecycle(Monkey child, Population population) { askForGrooming(child, environment.getParasiteInfection().make(), population); scheduleBreedings(child, population); kill(child, environment.getLifetime().make(), population);} void askForGrooming(Monkey child, Duration parasiteInfection, Population population) { schedule(new AskForGrooming(child, parasiteInfection, population));} private void scheduleBreedings(Monkey child, Population population) { final int childrenCount = RANDOM.nextInt(environment.getMaxChildren() + 1); IntStream. rangeClosed(1, childrenCount) .forEach(x -> breed(child, environment.getBreeding().make(), population));} void kill(Monkey child, Duration lifetime, Population population) { schedule(new Kill(child, lifetime, population));} private void breed(Monkey child, Duration breeding, Population population) { schedule(new Breed(child, breeding, population));} |
AskForGrooming , Kill , Breed и т. Д. Являются примерами уже упомянутого класса Action , например, Kill :
|
01
02
03
04
05
06
07
08
09
10
11
12
13
|
public class Kill extends MonkeyAction { private final Population population; public Kill(Monkey monkey, Duration lifetime, Population population) { super(monkey, lifetime); this.population = population; } @Override public void run(Monkey monkey) { population.kill(monkey); }} |
Я инкапсулирую все параметры моделирования в простой Environment значений класса, многие параметры, такие как parasiteInfection , lifetime или breeding , не являются константами, а являются экземплярами класса RandomPeriod :
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
|
@Valuepublic class RandomPeriod { private static final Random RANDOM = new Random(); Period expected; Period stdDev; public Duration make() { final long shift = Periods.toDuration(expected).toMillis(); final long stdDev = Periods.toDuration(this.stdDev).toMillis(); final double gaussian = RANDOM.nextGaussian() * stdDev; double randomMillis = shift + gaussian; return Duration.ofMillis((long) randomMillis); } } |
Это позволило мне охватить концепцию случайного периода времени с ожидаемым значением, стандартным отклонением и нормальным распределением . Метод make() просто генерирует один такой случайный период. Я не собираюсь исследовать полный исходный код этого моделирования, он доступен на GitHub . Теперь, наконец, пришло время запустить его несколько раз и понаблюдать за ростом (или вымиранием) населения. Кстати, я использую один и тот же планировщик и механизм действий, чтобы посмотреть, что происходит: я просто внедряю действие Probe один раз в год (логическое время!) И выводю текущий размер популяции.
Как и во многих циклах событий, должен быть только один поток, обращающийся к событиям. Мы придерживались этой практики, моделирование является однопоточным, поэтому нет необходимости выполнять какую-либо синхронизацию или блокировку, мы также можем использовать стандартные, небезопасные, но более быстрые коллекции. Меньше переключений контекста и улучшенная локальность кэша также помогают. Также мы можем легко вывести состояние симуляции на диск, например, чтобы восстановить его позже. Конечно, есть и недостатки. С тысячами обезьян симуляция замедляется, и мы ничего не можем с этим поделать, кроме тщательной оптимизации и покупки более быстрого процессора (даже не больше процессоров!)
Эксперимент
В качестве контрольной группы мы начинаем с крошечной (10 особей) популяции, состоящей исключительно из присосок и смеси присосок и скотин. В отсутствие мошенников эти два поведения неразличимы. Мы отключаем мутацию (вероятность того, что ребенок от присоски и скотины станет обманщиком, а не от присоски или скотины) и посмотрим, как растет популяция (ось X представляет время, ось Y — размер популяции):
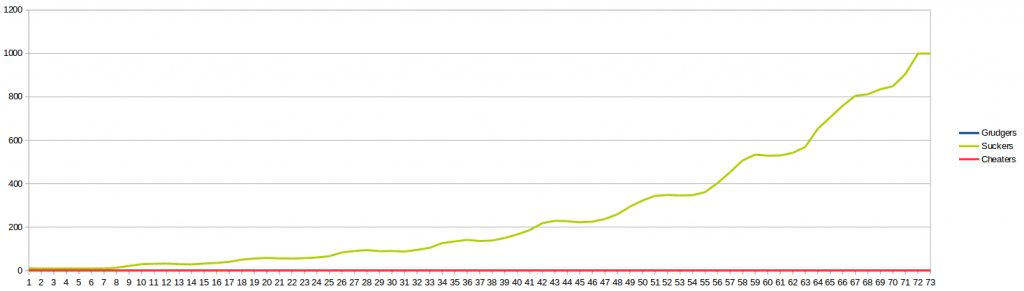
Обратите внимание, что доля лохов и недугов колеблется около 50%, поскольку эти два поведения ведут себя одинаково. Нет смысла проводить симуляцию только с несколькими читерами. Так как они обычно не ухаживают друг за другом, они быстро умирают, стирая « изменяющий ген ». С другой стороны, только присоски (без мутаций) растут в геометрической прогрессии (вы можете ясно видеть, как новые поколения рождаются после плато):
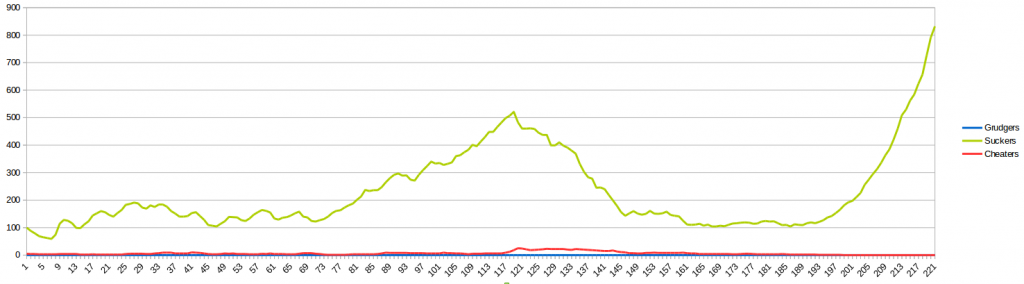
Однако что произойдет, если мы смоделируем население с 100 присосками и всего 5 обманщиками? Мутации снова отключены, чтобы сохранить чистоту симуляции:
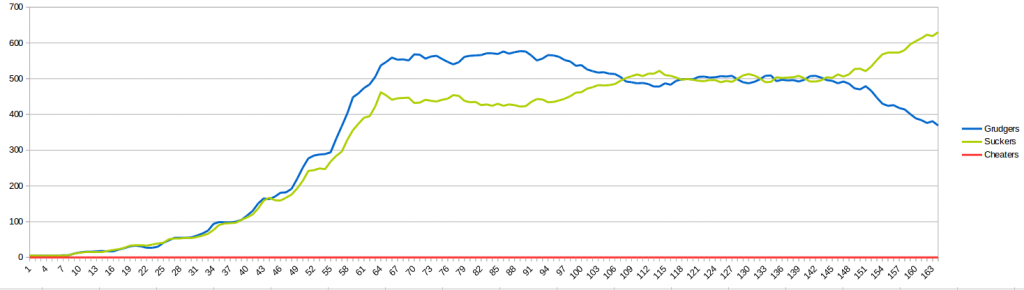
Есть два возможных сценария: либо ген мошенников исчезает, либо распространяется, что приводит к вымиранию населения. Это своего рода парадокс — если этот конкретный ген победит, вся популяция (включая этот ген!) Обречена. Теперь давайте смоделируем что-то более интересное. Мы включаем 5% вероятности мутаций и просим мошенников ухаживать в 9 из 10 случаев (чтобы они вели себя как присоски). Начнем со здоровой популяции из 5 присосок и 5 негодяев:
Видите ли вы, как грубияны быстро расширяются и почти всегда превосходят по численности присоски? Это потому, что присоски гораздо более уязвимы в среде, где мошенники иногда появляются из-за мутации. Вы заметили, как население быстро сокращается каждый раз, когда появляется небольшое количество присосок? Grudgers также уязвимы: они ухаживают за новорожденными обманщиками, еще не зная, кто они. Однако они не повторяют эту ошибку, как лохи. Вот почему лохи всегда болеют, но они не вымирают полностью, потому что они в некоторой степени защищены негодяями. Не напрямую, но злодеи убивают мошенников, не ухаживая за ними, уменьшая угрозу. Вот как взаимодействуют разные модели поведения. Так почему же все-таки вымерло население? Посмотрите внимательно на конец таблицы, в какой-то момент по случайной причине присоски превзошли численностью недоброжелателей — это было особенно возможно в отсутствие мошенников в то время. Итак, что случилось? Несколько мошенников появились внезапно из-за мутации, и это общество обезьян было обречено.
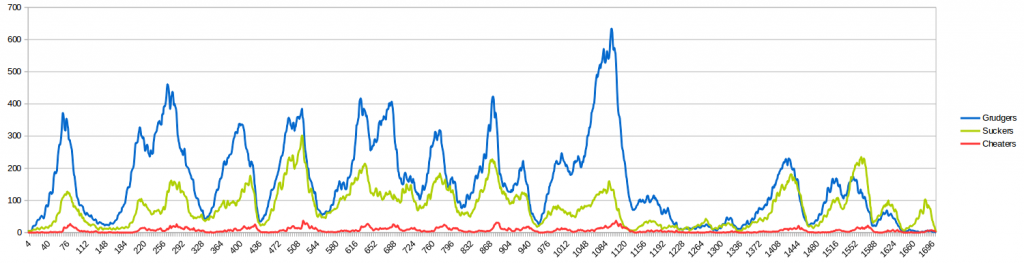
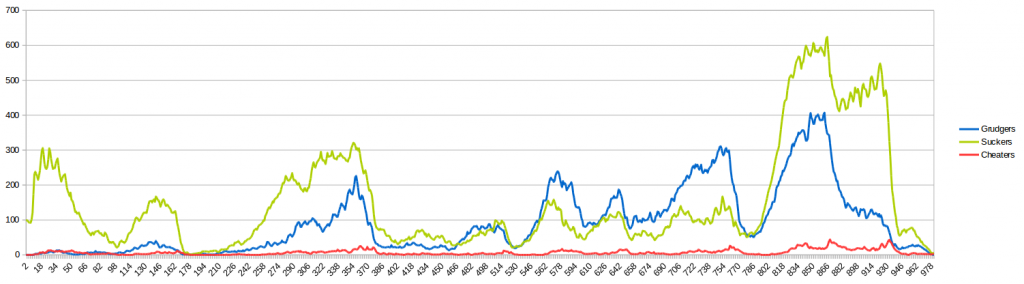
Теперь давайте рассмотрим другой пример: зрелое общество, в котором уже живут 100 присосок, других видов поведения не наблюдается. Конечно из-за мутации быстро появляются негодяи и мошенники. В большинстве случаев это моделирование заканчивается очень быстро, через несколько поколений. Вероятность рождения мошенника такая же, как и вероятность грубияна, но нам нужно гораздо больше грубых, чтобы защитить лохов. Таким образом, население умирает. Но мне удалось провести несколько симуляций, где такое общество какое-то время действительно существовало:
Интересно, что присоски доминировали в популяции довольно долгое время, но еще одна эпидемическая атака мошенников убила большинство присосок. К сожалению, последний рост числа мошенников привел к тому, что количество недоброжелателей дошло до того, что они уже не могли защитить лохов и внезапно все умирают.
Резюме
С точки зрения реализации использование однопоточной модели и очереди действий работало действительно хорошо, несмотря на сложность масштабирования. Однако биологические выводы гораздо интереснее:
- Альтруистическое население (только лохи ) может жить счастливо вечно, пока нет мошенников, пытающихся использовать систему
- Присутствие одного мошенника в альтруистической популяции может привести к ее разрушению.
- Население нуждается в охранниках, которые защищают от мошенников
- Даже в присутствии охранников есть место для небольшого количества читеров, которые остаются незамеченными
- Если число мошенников превышает какое-то критическое соотношение, население больше не может себя защитить и сдается. Каждый образец умирает, включая мошенников
- Гены, которые обычно вредны для вымершей популяции, даже если это затягивает всю популяцию
Вы можете распространять выводы для человеческого общества.
- Полный исходный код доступен на GitHub, не стесняйтесь экспериментировать, также приветствуются запросы на извлечение!
| Ссылка: | Биологическое компьютерное моделирование эгоистичных генов от нашего партнера JCG Томаша Нуркевича в блоге Java и соседстве . |