Одной из захватывающих вещей в 1980-х годах было программирование симуляций для решения сложных аналитических задач, и одним из наиболее полезных методов был запуск симуляции Монте-Карло. Этот подход многократно запускает моделирование, чтобы рассчитать наиболее вероятный результат.
Хотя PHP не известен как научный или исследовательский язык программирования, симуляции Монте-Карло можно легко написать в веб-приложении PHP. В этой статье я покажу вам как.
Проблема реального мира
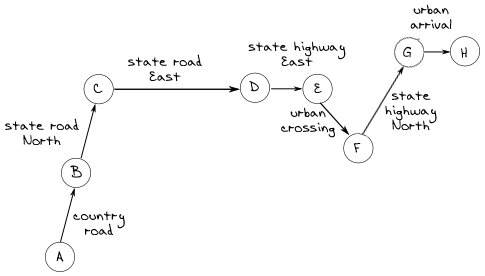
Позавчера у меня была встреча в 9:00, примерно в 100 милях от моего дома. В 6:30 я проснулся и оделся, а во время завтрака я начал тренироваться следующие несколько часов на блокноте. Я, очевидно, хотел прибыть на встречу безопасно и вовремя, поэтому я начал делать набросок разбивки на восемь этапов: городской выезд, проселочная дорога, государственная дорога на север, государственная дорога на восток, государственная трасса на восток, городской переход, государственная трасса на север и городское прибытие. Эскиз более или менее выглядел так:
Накануне вечером моя жена наполнила бензобак, и в идеале я мог выехать прямо на проселочную дорогу. Когда я смотрел на них, шины казались нормальными, но сомневаюсь, что мне нужно было сделать 10-минутный обход, чтобы должным образом проверить их давление. Если бы я остановился и проверил шины, я был бы уверен в их давлении. Иначе мне пришлось бы путешествовать с неопределенностью. Плохое давление в шинах может повлиять на мою устойчивость и скорость вождения.
Я мог уйти уже в 6:40, но тогда моей жене пришлось бы брать нашу дочь в школу, а не идти прямо на работу. Если бы я подождал еще 10 минут, я мог бы быть в школе, поскольку их ворота открылись на утро и избавили мою жену от неприятностей. Школа уже выезжает из города, поэтому не будет значительного дополнительного времени в пути.
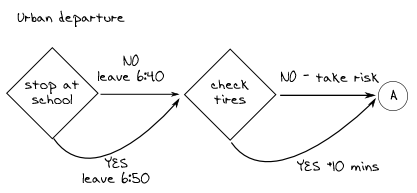
Я вернулся к своему рисунку и добавил следующее:
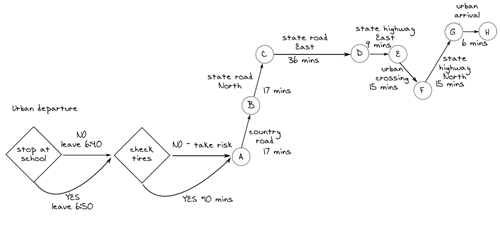
Потягивая вторую чашку кофе, я стоял у окна. Чистое сумеречное небо и бодрый утренний ветерок согласились с идеальным прогнозом дня на моем смартфоне, который заставил меня поверить, что поездка будет быстрой. Чтобы закончить планирование, я использовал прошлый опыт и записал примерное время поездки:
Ожидаемое время в пути составило 115 минут (1 час 55 минут), которые я мог покрыть без остановок. Мой ETA был 8:35, если я уехал прямо на дорогу, и 8:55, если я решил взять мою дочь в школу и проверить шины.
Но ни один план не доживет до первой встречи с врагом! По какой-то таинственной причине многие другие родители решили бросить своих детей в школу раньше, чем обычно, и я потерял более 5 минут на то, что планировалось как быстрый обход. Зная, что моя базовая линия уже была скомпрометирована, я решил пропустить проверку шин и поехать прямо к проселочной дороге.
Я достиг дороги на пять минут раньше, чем предполагалось в первоначальном наихудшем случае, и поездка шла хорошо, пока где-то между вехами B и C я не столкнулся с густым туманом, который уменьшил мою видимость. Это уменьшило мою среднюю скорость и усложнило обгон медленных, но длинных грузовиков.
Городское движение в городе, через который я должен был перейти, было намного легче, чем обычно, и мне понадобилось не более 10 минут, чтобы пересечь его. И в нескольких милях от шоссе на юг туман поднялся, и я смог ехать на полной легальной скорости. Но когда я приблизился к месту назначения, я понял, что некоторые дорожные работы, которые велись, заблокировали выезд, который я планировал сделать. Это добавило еще 10 минут к моему времени в пути и, разумеется, я опоздал.
Моделирование поездки в PHP
Я считаю, что большая часть PHP-кодирования предназначена для коммерческих и некоммерческих бизнес-сайтов. Но PHP может быть прекрасным инструментом для научных исследований, и с таким же успехом его легче обучать непрофессиональным программистам, таким как инженеры и ученые, чем другим языкам, таким как мой любимый Python.
Давайте напишем основной код, который поможет мне понять, насколько раньше или позже я мог прийти на собрание, если бы один или несколько этапов моего плана существенно отличались от их базовых оценок. Мы можем начать моделировать поездку следующим образом:
<?php
class MyTrip
{
protected $departureTime;
protected $meetingTime;
protected $travelTimes;
public function __construct() {
$this->setDepartureTime('0640');
$this->setMeetingTime('0900');
// travel times in minutes between milestones
$this->setTravelTimes(array(
'AB' => 17,
'BC' => 17,
'CD' => 36,
'DE' => 9,
'EF' => 15,
'FG' => 15,
'GH' => 6
));
}
// for convenience convert time string to minutes past
// midnight
protected static function convertToMinutes($timeStr) {
return substr($timeStr, 0, 2) * 60 +
substr($timeStr, 2, 2);
}
public function setDepartureTime($timeStr) {
$this->departureTime = self::convertToMinutes($timeStr);
}
public function setMeetingTime($timeStr) {
$this->meetingTime = self::convertToMinutes($timeStr);
}
public function setTravelTimes(array $travelTimes) {
$this->travelTimes = $travelTimes;
}
public checkPlan($stopAtSchool = true, $checkTires = true) {
// ...
}
} Планы должны быть выполнимыми, и подходящим критерием для оценки этого является то, является ли сумма всех времен плюс самое раннее время отправления меньше или равна времени собрания. Вот что определяет метод checkPlan()
<?php
public checkPlan($stopAtSchool = true, $checkTires = true) {
// calculate the sum of travel times between milestones
$travelTime = array_sum($this->travelTimes);
// add delay if dropping kid off at school
$schoolDelay = ($stopAtSchool) ? 10 : 0;
// add delay if checking tire pressure
$tiresDelay = ($checkTires) ? 10 : 0;
// find the total schedule baseline
$meetingArriveTime = $this->departureTime + $travelTime +
$schoolDelay + $tiresDelay;
// does the traveller make the meeting on time?
$arriveOnTime = $meetingArriveTime <= $this->meetingTime;
return array($meetingArriveTime, $this->meetingTime,
$arriveOnTime);
}
Теперь все, что нам нужно сделать, это создать экземпляр класса и попросить его проверить мой план:
<?php
$trip = new MyTrip();
print_r($trip->checkPlan());
Учитывая значения по умолчанию, выше будет выводить, что мой первоначальный план был в порядке:
массив ( [0] => 535 [1] => 540 [2] => 1 )
Я должен быть там через 535 минут после полуночи, а встреча происходит через 540 минут после полуночи. Согласно исходным данным, я прибуду на собрание в 8:45, всего за 5 минут до назначенного времени!
Но как насчет неизбежных изменений? Как мы можем объяснить неопределенные элементы?
Монте-Карло и добавление случайности
Очень упрощенно мы можем определить запас прочности для каждого события и сказать, что это может произойти на 10% раньше и на 25% позже запланированного времени. Такие поля могут быть случайным образом добавлены к задержкам вылета и каждому времени в пути между этапами путем умножения каждого фактора на rand(90,125)/100
Мы также можем назначить 50% вероятности, что оба решения бросят мою дочь в школу и проверят шины. Снова нам помогает функция rand()
$this->checkTires = rand(1, 100) > 50;
Собрав все это вместе, мы можем определить метод checkPlanRisk()
<?php
public function checkPlanRisk() {
// adjust and sum travel times between milestones
$travelTime = 0;
foreach ($this->travelTimes as $t) {
$travelTime += $t * rand(90, 125) / 100;
}
// decide whether to drop kid off at school and randomly set
// the delay time
$schoolDelay = 0;
if (rand(1, 100) > 50) {
$schoolDelay = 10 * rand(90, 125) / 100;
}
// ditto for checking tires
$tiresDelay = 0;
if (rand(1, 100) > 50) {
$tiresDelay = 10 * rand(90, 125) / 100;
}
// find the total schedule baseline
$meetingArriveTime = $this->departureTime + $travelTime +
$schoolDelay + $tiresDelay;
// does the traveller make the meeting on time?
$arriveOnTime = $meetingArriveTime <= $this->meetingTime;
return array($schoolDelay, $tiresDelay, $meetingArriveTime,
$this->meetingTime, $arriveOnTime);
}
Теперь возникает вопрос, насколько вероятно, что путешественник прибудет вовремя, учитывая начальные условия и предполагаемую неопределенность? Моделирование методом Монте-Карло дает ответ на этот вопрос, выполняя большое количество раз и вычисляя «уровень достоверности», определяемый как отношение числа прибывших вовремя к общему количеству испытаний.
Если мы запустим этот метод достаточное количество раз и запишем, как часто путешественник прибывает вовремя, мы можем установить некоторый запас уверенности в том, что поездка осуществима, как планировалось.
<?php
public function runCheckPlanRisk($numTrials) {
$arriveOnTime = 0;
for ($i = 1; $i <= $numTrials; $i++) {
$result = $this->checkPlanRisk();
if ($result[4]) {
$arriveOnTime++;
}
echo "Trial: " . $i;
echo " School delay: " . $result[0];
echo " Tire delay: " . $result[1];
echo " Enroute time: " . $result[2];
if ($result[4]) {
echo " -- Arrive ON TIME";
}
else {
echo " -- Arrive late";
}
$confidence = $arriveOnTime / $i;
echo "nConfidence level: $confidencenn";
}
}
Создать новый экземпляр MyTrip
<?php
$trip = new MyTrip();
$trip->runCheckPlanRisk(1000);
Результатом будет распечатка с 1000 записей, например:
Пробная версия: 1000 Школьная задержка: 0 Задержка шин: 11,3 Время в пути: 530,44 - Прибытие по времени Уровень доверия: 0.716
С указанными выше параметрами уровень достоверности, по-видимому, приближается к 0,72, что примерно указывает на то, что у путешественника есть 72% шансов попасть на встречу вовремя.
Grosso modo , Monte Carlo полагается на сходимость среднего результата последовательности идентичных экспериментов. Средний результат также известен как ожидаемое значение и может рассматриваться как вероятность достижения желаемого результата. Конечно, это довольно старая концепция, и такие симуляции были сделаны задолго до появления цифрового компьютера.
Вывод
Сегодня в нашем распоряжении имеются чрезвычайно мощные ресурсы и очень удобный язык, такой как PHP, который можно использовать для создания как логики симуляции, так и удобного для пользователя веб-интерфейса. С помощью нескольких строк кода мы создали модель и применили к ней моделирование по методу Монте-Карло, что дало понятный результат, полезный для бизнес-решений. Это область, которую стоит изучить, и было бы неплохо увидеть некоторые функции научных вычислений, добавленные в PHP, чтобы ученые и инженеры могли воспользоваться преимуществами этого универсального, нонсенс-языка.
Код для этой статьи доступен на GitHub.
Изображение через Fotolia