Структуры данных для разработчиков PHP: куча

В прошлой паре статей я познакомил вас с тремя основными структурами данных: стек, очередь и дерево . В этой статье я познакомлю вас с другим абстрактным типом данных, который тесно связан: куча. Кучи — это специализированные древовидные структуры данных, которые удовлетворяют свойству кучи — значение узла (ключ) любого родителя всегда упорядочено относительно значений его дочерних узлов по всему дереву. Давайте внимательнее посмотрим!

Кучи

Есть несколько вариантов кучи. Например, если родительские ключи упорядочены таким образом, что они имеют равное или большее значение, чем их дочерние элементы, и самый высокий ключ находится в корне, куча называется maxheap . Если родительские ключи упорядочены так, что они имеют равное или более низкое значение, чем их дочерние элементы, с самым низким ключом в корне, куча называется minheap . SPL (PHP> = 5.3.0) предоставляет базовую кучу, minheap, maxheap и специализированный тип данных, называемый приоритетной очередью.

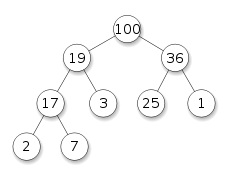
Итак, вот пример того, как выглядит куча:

На рисунке выше изображена полная двоичная maxheap. Это двоичный файл, потому что каждый узел имеет ровно два дочерних элемента, и maxheap, потому что ключ с самым высоким значением находится в корневом узле, а все родительские узлы имеют значения, превышающие их дочерние элементы.

Хотя кучи обычно реализуются как полные двоичные деревья, в отличие от двоичных деревьев не существует подразумеваемого упорядочения братьев и сестер и двоюродных братьев, а также нет никакой подразумеваемой последовательности для обхода по порядку.

Кучи являются вариантом типа данных таблицы, поэтому они также имеют те же основные операции:

• создать — создать пустую кучу.
• isEmpty — определить, пуста ли куча.
• вставить — добавить элемент в кучу.
• Извлечь — удалить самый верхний элемент (корневой) из кучи.

В отличие от таблицы, операции извлечения и удаления для кучи объединяются в одну операцию извлечения, поэтому давайте сосредоточимся на том, как операция извлечения работает в первую очередь.

Условием удаления элемента из кучи является то, что мы можем удалить только корневой узел. Допустим, мы удалили корневой узел (100) из приведенного выше примера. Мы остались бы с двумя непересекающимися кучами. Нам нужен метод преобразования оставшихся узлов обратно в одну кучу после удаления корня. Присоединение к ним легко осуществить, переместив последний узел в корень, но у нас осталась получившаяся структура, которая не имеет свойства heap. Такая структура называется полугрудом .

Теперь нам нужен способ превратить полугучи в кучу. Одна стратегия состоит в том, чтобы опустить корневой элемент вниз по дереву, пока он не достигнет узла, где он не будет не на своем месте. Мы итеративно сравниваем значение корневого узла с его потомками и меняемся местами с более крупным потомком, пока он не достигнет узла, где ни один из потомков не имеет большего (или равного) значения, чем он сам.

Реализация кучи как массива

Мы можем наивно реализовать бинарный maxheap как массив. У двоичного боде не более двух дочерних элементов, поэтому для любого n числа узлов двоичная куча будет иметь не более 2n + 1 узлов.

Вот как выглядит реализация:

<?php
class BinaryHeap
{
    protected $heap;

    public function __construct() {
        $this->heap  = array();
    }

    public function isEmpty() {
        return empty($this->heap);
    }

    public function count() {
        // returns the heapsize
        return count($this->heap) - 1;
    }

    public function extract() {
        if ($this->isEmpty()) {
            throw new RunTimeException('Heap is empty');
        }

        // extract the root item
        $root = array_shift($this->heap);

        if (!$this->isEmpty()) {
            // move last item into the root so the heap is
            // no longer disjointed
            $last = array_pop($this->heap);
            array_unshift($this->heap, $last);

            // transform semiheap to heap
            $this->adjust(0);
        }

        return $root;
    }

    public function compare($item1, $item2) {
        if ($item1 === $item2) {
            return 0;
        }
        // reverse the comparison to change to a MinHeap!
        return ($item1 > $item2 ? 1 : -1);
    }

    protected function isLeaf($node) {
        // there will always be 2n + 1 nodes in the
        // sub-heap
        return ((2 * $node) + 1) > $this->count();
    }

    protected function adjust($root) {
        // we've gone as far as we can down the tree if
        // root is a leaf
        if (!$this->isLeaf($root)) {
            $left  = (2 * $root) + 1; // left child
            $right = (2 * $root) + 2; // right child

            // if root is less than either of its children
            $h = $this->heap;
            if (
              (isset($h[$left]) &&
                $this->compare($h[$root], $h[$left]) < 0)
              || (isset($h[$right]) &&
                $this->compare($h[$root], $h[$right]) < 0)
            ) {
                // find the larger child
                if (isset($h[$left]) && isset($h[$right])) {
                  $j = ($this->compare($h[$left], $h[$right]) >= 0)
                      ? $left : $right;
                }
                else if (isset($h[$left])) {
                  $j = $left; // left child only
                }
                else {
                  $j = $right; // right child only
                }

                // swap places with root
                list($this->heap[$root], $this->heap[$j]) = 
                  array($this->heap[$j], $this->heap[$root]);

                // recursively adjust semiheap rooted at new
                // node j
                $this->adjust($j);
            }
        }
    }
}

Стратегия вставки является полной противоположностью извлечения: мы вставляем элемент в конец кучи и добавляем его в нужное место. Поскольку мы знаем, что полное двоичное дерево с полным последним уровнем содержит n / 2 + 1 узлов, мы можем пройти через кучу с помощью простого двоичного поиска.

 public function insert($item) {
    // insert new items at the bottom of the heap
    $this->heap[] = $item;

    // trickle up to the correct location
    $place = $this->count();
    $parent = floor($place / 2);
    // while not at root and greater than parent
    while (
      $place > 0 && $this->compare(
        $this->heap[$place], $this->heap[$parent]) >= 0
    ) {
        // swap places
        list($this->heap[$place], $this->heap[$parent]) =
            array($this->heap[$parent], $this->heap[$place]);
        $place = $parent;
        $parent = floor($place / 2);
    }
}

 <?php
$heap = new BinaryHeap();
$heap->insert(19);
$heap->insert(36);
$heap->insert(54);
$heap->insert(100);
$heap->insert(17);
$heap->insert(3);
$heap->insert(25);
$heap->insert(1);
$heap->insert(67);
$heap->insert(2);
$heap->insert(7);

  массив
 (
     [0] => 100
     [1] => 67
     [2] => 54
     [3] => 36
     [4] => 19
     [5] => 7
     [6] => 25
     [7] => 1
     [8] => 17
     [9] => 2
     [10] => 3
 ) 

 <?php
while (!$heap->isEmpty()) {
    echo $heap->extract() . "n";
}

  100
 67
 54
 36
 25
 19
 17
 7
 3
 2
 1 

 <?php
class MyHeap extends SplMaxHeap
{
    public function compare($item1, $item2) {
        return (int) $item1 - $item2;
    }
}

 <?php
class PriQueue extends SplPriorityQueue
{
    public function compare($p1, $p2) {
        if ($p1 === $p2) return 0;
        // in ascending order of priority, a lower value
        // means higher priority
        return ($p1 < $p2) ? 1 : -1;
   }
}

 <?php
$pq = new PriQueue();
$pq->insert('A', 4);
$pq->insert('B', 3);
$pq->insert('C', 5);
$pq->insert('D', 8);
$pq->insert('E', 2);
$pq->insert('F', 7);
$pq->insert('G', 1);
$pq->insert('H', 6);
$pq->insert('I', 0);
 
while ($pq->valid()) {
    print_r($pq->current());
    echo "n";
    $pq->next();
}

  я
 грамм
 Е
 В

 С
 ЧАС
 F
 D 

 <?php
// extract just the priority
$pq->setExtractFlags(SplPriorityQueue::EXTR_PRIORITY);

// extract both data and priority (returns an associative
// array for each element)
$pq->setExtractFlags(SplPriorityQueue::EXTR_BOTH);