В одной из моих предыдущих статей я познакомил вас с древовидной структурой данных . Теперь я хотел бы изучить связанную структуру — график. Графики имеют ряд реальных приложений, таких как оптимизация сети, маршрутизация трафика и анализ социальных сетей. Google PageRank, Facebook Graph Graph Search и рекомендации Amazon и NetFlix являются некоторыми примерами приложений, основанных на графике.
В этой статье я расскажу о двух распространенных проблемах, в которых используются графики, — задачах с наименьшим количеством прыжков и кратчайшим путем.
График — это математическая конструкция, используемая для моделирования отношений между парами ключ / значение. Граф содержит набор вершин (узлов) и произвольное количество ребер (линий), которые их соединяют. Эти края могут быть направлены или не направлены. Направленное ребро — это просто ребро между двумя вершинами, и ребро A → B не считается тем же, что B → A. Ненаправленный край не имеет ориентации или направления; ребро AB эквивалентно BA. Древовидная структура, о которой мы узнали в прошлый раз, может рассматриваться как тип неориентированного графа, где каждая вершина соединена хотя бы с одной другой вершиной простым путем.
Графики также могут быть взвешенными или не взвешенными. Взвешенный график или сеть — это график, в котором весу или стоимости присваивается каждому из его ребер. Взвешенные графики обычно используются при определении наиболее оптимального пути, наиболее целесообразного или самого дешевого пути между двумя точками. Направления движения GoogleMap — это пример, в котором используются взвешенные графики.
Наименьшее количество прыжков
Обычное применение теории графов — нахождение наименьшего числа прыжков между любыми двумя узлами. Как и в случае с деревьями, графики можно просматривать одним из двух способов: сначала в глубину, либо в ширину. Мы рассмотрели поиск в глубину в предыдущей статье, поэтому давайте рассмотрим поиск в ширину.
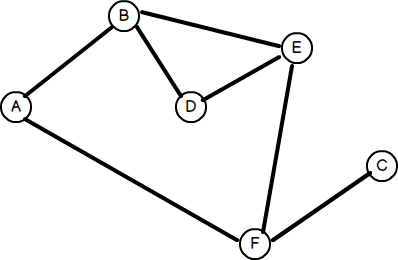
Рассмотрим следующий график:
Для простоты предположим, что граф не является ненаправленным, то есть ребра в любом направлении идентичны. Наша задача — найти наименьшее количество прыжков между любыми двумя узлами.
При поиске в ширину мы начинаем с корневого узла (или любого узла, обозначенного как корневой) и проходим вниз по дереву уровень за уровнем. Для этого нам нужна очередь для ведения списка не посещенных узлов, чтобы мы могли возвращаться и обрабатывать их после каждого уровня.
Общий алгоритм выглядит так:
1. Создайте очередь 2. Поставьте в очередь корневой узел и отметьте его как посещенный. 3. Пока очередь не пуста, выполните: 3a. освободить текущий узел 3b. если текущий узел - тот, который мы ищем, тогда остановитесь 3в. еще поставьте в очередь каждый не посещенный соседний узел и отметьте как посещенный
Но как мы узнаем, какие узлы являются смежными, не говоря уже о том, что они не посещены, не пройдя сначала график? Это подводит нас к проблеме того, как графическая структура данных может быть смоделирована.
Представление графа
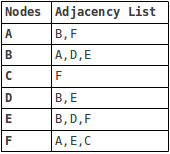
Обычно существует два способа представления графа: либо в виде матрицы смежности, либо в виде списка смежности. Приведенный выше график, представленный в виде списка смежности, выглядит следующим образом:
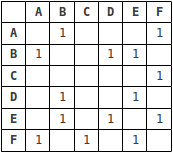
Представленный в виде матрицы, график выглядит следующим образом, где 1 указывает «падение» ребра между 2 вершинами:
Списки смежности более экономичны, особенно для разреженных графов, в которых большинство пар вершин не связаны, а матрицы смежности способствуют более быстрому поиску. В конечном счете, выбор представления будет зависеть от того, какой тип графовых операций может потребоваться.
Давайте использовать список смежности для представления графа:
<?php $graph = array( 'A' => array('B', 'F'), 'B' => array('A', 'D', 'E'), 'C' => array('F'), 'D' => array('B', 'E'), 'E' => array('B', 'D', 'F'), 'F' => array('A', 'E', 'C'), ); А теперь давайте посмотрим, как выглядит реализация общего алгоритма поиска в ширину:
<?php class Graph { protected $graph; protected $visited = array(); public function __construct($graph) { $this->graph = $graph; } // find least number of hops (edges) between 2 nodes // (vertices) public function breadthFirstSearch($origin, $destination) { // mark all nodes as unvisited foreach ($this->graph as $vertex => $adj) { $this->visited[$vertex] = false; } // create an empty queue $q = new SplQueue(); // enqueue the origin vertex and mark as visited $q->enqueue($origin); $this->visited[$origin] = true; // this is used to track the path back from each node $path = array(); $path[$origin] = new SplDoublyLinkedList(); $path[$origin]->setIteratorMode( SplDoublyLinkedList::IT_MODE_FIFO|SplDoublyLinkedList::IT_MODE_KEEP ); $path[$origin]->push($origin); $found = false; // while queue is not empty and destination not found while (!$q->isEmpty() && $q->bottom() != $destination) { $t = $q->dequeue(); if (!empty($this->graph[$t])) { // for each adjacent neighbor foreach ($this->graph[$t] as $vertex) { if (!$this->visited[$vertex]) { // if not yet visited, enqueue vertex and mark // as visited $q->enqueue($vertex); $this->visited[$vertex] = true; // add vertex to current path $path[$vertex] = clone $path[$t]; $path[$vertex]->push($vertex); } } } } if (isset($path[$destination])) { echo "$origin to $destination in ", count($path[$destination]) - 1, " hopsn"; $sep = ''; foreach ($path[$destination] as $vertex) { echo $sep, $vertex; $sep = '->'; } echo "n"; } else { echo "No route from $origin to $destinationn"; } } }
Запустив следующие примеры, мы получим:
<?php $g = new Graph($graph); // least number of hops between D and C $g->breadthFirstSearch('D', 'C'); // outputs: // D to C in 3 hops // D->E->F->C // least number of hops between B and F $g->breadthFirstSearch('B', 'F'); // outputs: // B to F in 2 hops // B->A->F // least number of hops between A and C $g->breadthFirstSearch('A', 'C'); // outputs: // A to C in 2 hops // A->F->C // least number of hops between A and G $g->breadthFirstSearch('A', 'G'); // outputs: // No route from A to G
Если бы мы использовали стек вместо очереди, обход становится поиском в глубину.
Нахождение кратчайшего пути
Другая распространенная проблема — найти наиболее оптимальный путь между любыми двумя узлами. Ранее я упомянул направление движения GoogleMap в качестве примера этого. Другие приложения включают планирование маршрутов, управление дорожным движением и планирование движения поездов / автобусов.
Один из самых известных алгоритмов для решения этой проблемы был изобретен в 1959 году 29-летним программистом по имени Эдсгер В. Дейкстра. В общих чертах, решение Дейкстры включает изучение каждого ребра между всеми возможными парами вершин, начиная с исходного узла и поддерживая обновленный набор вершин с наименьшим общим расстоянием, пока целевой узел не будет достигнут или не достигнут, в зависимости от того, в каком случае это происходит.
Существует несколько способов реализации этого решения, и, действительно, за годы, прошедшие после 1959 года, многие улучшения — с использованием MinHeaps, PriorityQueues и Fibonacci Heaps — были внесены в оригинальный алгоритм Дейкстры. Некоторые улучшили производительность, в то время как другие были разработаны для устранения недостатков в решении Дейкстры, поскольку оно работало только с положительно взвешенными графиками (где веса — положительные значения).
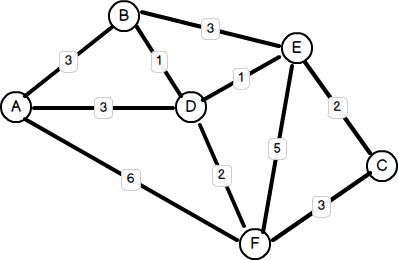
Вот пример (положительного) взвешенного графика:
Мы можем представить этот граф в виде списка смежности следующим образом:
<?php $graph = array( 'A' => array('B' => 3, 'D' => 3, 'F' => 6), 'B' => array('A' => 3, 'D' => 1, 'E' => 3), 'C' => array('E' => 2, 'F' => 3), 'D' => array('A' => 3, 'B' => 1, 'E' => 1, 'F' => 2), 'E' => array('B' => 3, 'C' => 2, 'D' => 1, 'F' => 5), 'F' => array('A' => 6, 'C' => 3, 'D' => 2, 'E' => 5), );
А вот реализация, использующая PriorityQueue для поддержки списка всех «неоптимизированных» вершин:
<?php class Dijkstra { protected $graph; public function __construct($graph) { $this->graph = $graph; } public function shortestPath($source, $target) { // array of best estimates of shortest path to each // vertex $d = array(); // array of predecessors for each vertex $pi = array(); // queue of all unoptimized vertices $Q = new SplPriorityQueue(); foreach ($this->graph as $v => $adj) { $d[$v] = INF; // set initial distance to "infinity" $pi[$v] = null; // no known predecessors yet foreach ($adj as $w => $cost) { // use the edge cost as the priority $Q->insert($w, $cost); } } // initial distance at source is 0 $d[$source] = 0; while (!$Q->isEmpty()) { // extract min cost $u = $Q->extract(); if (!empty($this->graph[$u])) { // "relax" each adjacent vertex foreach ($this->graph[$u] as $v => $cost) { // alternate route length to adjacent neighbor $alt = $d[$u] + $cost; // if alternate route is shorter if ($alt < $d[$v]) { $d[$v] = $alt; // update minimum length to vertex $pi[$v] = $u; // add neighbor to predecessors // for vertex } } } } // we can now find the shortest path using reverse // iteration $S = new SplStack(); // shortest path with a stack $u = $target; $dist = 0; // traverse from target to source while (isset($pi[$u]) && $pi[$u]) { $S->push($u); $dist += $this->graph[$u][$pi[$u]]; // add distance to predecessor $u = $pi[$u]; } // stack will be empty if there is no route back if ($S->isEmpty()) { echo "No route from $source to $targetn"; } else { // add the source node and print the path in reverse // (LIFO) order $S->push($source); echo "$dist:"; $sep = ''; foreach ($S as $v) { echo $sep, $v; $sep = '->'; } echo "n"; } } }
Как видите, решение Дейкстры — это просто вариант поиска в ширину!
Выполнение следующих примеров дает следующие результаты:
<?php $g = new Dijkstra($graph); $g->shortestPath('D', 'C'); // 3:D->E->C $g->shortestPath('C', 'A'); // 6:C->E->D->A $g->shortestPath('B', 'F'); // 3:B->D->F $g->shortestPath('F', 'A'); // 5:F->D->A $g->shortestPath('A', 'G'); // No route from A to G
Резюме
В этой статье я представил основы теории графов, два способа представления графов и две фундаментальные проблемы в применении теории графов. Я показал вам, как поиск в ширину используется, чтобы найти наименьшее количество прыжков между любыми двумя узлами, и как решение Дейкстры используется для поиска кратчайшего пути между любыми двумя узлами.
Изображение через Fotolia