В предыдущей статье я представил две основные структуры данных: стек и очередь. Статья была хорошо принята, поэтому я решил поделиться структурами данных в периодической серии здесь, на SitePoint. В этой записи я познакомлю вас с деревьями, другой структурой данных, используемой в разработке программного обеспечения и архитектуре. Другие статьи и структуры данных будут следовать!
Задача поиска
Управление структурой данных обычно включает 3 типа операций:
- вставка — операции, которые вставляют данные в структуру.
- удаление — операции, которые удаляют данные из структуры.
- traversal — операции, которые извлекают данные из структуры.
В случае стеков и очередей эти операции ориентированы на положение, то есть они ограничены положением элемента в структуре. Но что, если нам нужно хранить и извлекать данные по их значению?
Рассмотрим следующий список (в произвольном порядке):
Очевидно, что ни стек, ни очередь не подойдут; мы потенциально должны были бы пересечь всю структуру, чтобы найти конкретную запись, если значение является последним в списке или отсутствует в списке вообще. Предполагая, что требуемое значение находится в списке, и что каждый элемент с равной вероятностью будет содержать требуемое значение, нам нужно будет посетить в среднем n / 2 элементов — где n — длина списка. Чем длиннее список, тем больше времени потребуется, чтобы найти то, что мы ищем. В этом случае требуется возможность упорядочить данные таким образом, чтобы облегчить поиск, в который входят деревья.
Мы можем абстрагировать эти данные в виде «таблицы» с помощью следующих основных операций:
- создать — создать пустую таблицу.
- вставить — добавить элемент в таблицу.
- удалить — удалить элемент из таблицы.
- восстановить — найти элемент в таблице.
Если это выглядит примерно как операции создания, чтения, обновления, удаления (CRUD) базы данных, то это потому, что деревья тесно связаны с базами данных и тем, как они представляют записи данных внутри.
Один из способов, которым мы можем представить нашу «таблицу», — это линейная реализация, которая отражает плоский, похожий на список вид таблицы. Линейные реализации могут быть как отсортированными, так и несортированными, а также последовательными (т.е. записи фиксированной длины или переменной длины с использованием разделителей записей) или связанными (с использованием указателей записей). Что бы это ни стоило, ранние разработки баз данных, такие как метод индексированного последовательного доступа IBM (ISAM) и устаревшие файловые системы, такие как таблица размещения файлов MS-DOS (FAT), были основаны на линейных реализациях.
Недостатком последовательных реализаций является то, что они являются более дорогостоящими с точки зрения вставки и удаления, тогда как связанные реализации допускают динамическое распределение памяти. Поиск последовательной реализации фиксированной длины, однако, значительно более эффективен, чем связанная реализация, поскольку он может облегчить бинарный поиск.
деревья
Итак, как мы узнали, иногда может быть более эффективно использовать реализацию нелинейного поиска, такую как дерево. Деревья предоставляют лучшие возможности как последовательных, так и связанных реализаций таблиц и очень эффективно поддерживают все операции с таблицами. По этой причине многие современные базы данных и файловые системы теперь используют деревья для облегчения индексации. Например, механизм хранения MyISAM MySQL использует деревья для индексов, а Apple HFS +, Microsoft NTFS и btrfs для Linux используют деревья для индексации каталогов.
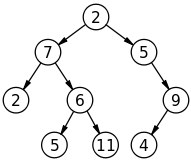
Как видите, деревья, как правило, являются иерархическими и подразумевают отношения родитель-потомок между узлами. Узел без родителей называется корнем , а узел без детей называется листом . Дочерние узлы одного и того же родителя называются братьями и сестрами . Термин ребра относится к соединениям (обозначены стрелками) между узлами.
Вы заметите, что двоичное дерево на рисунке выше является разновидностью двусвязного списка. На самом деле, если бы мы переставили узлы, чтобы сгладить дерево, это выглядело бы в точности как двусвязный список!
Узел, имеющий не более двух дочерних элементов, является самой простой формой дерева, и мы можем использовать это свойство для создания двоичного дерева в виде рекурсивной коллекции двоичных узлов:
<?php
class BinaryNode
{
public $value; // contains the node item
public $left; // the left child BinaryNode
public $right; // the right child BinaryNode
public function __construct($item) {
$this->value = $item;
// new nodes are leaf nodes
$this->left = null;
$this->right = null;
}
}
class BinaryTree
{
protected $root; // the root node of our tree
public function __construct() {
$this->root = null;
}
public function isEmpty() {
return $this->root === null;
}
}Вставка узлов
Добавление элементов в дерево немного более «интересно». Есть несколько решений, многие из которых включают вращение и восстановление баланса дерева. Действительно, различные древовидные структуры, такие как AVL, Red-Black и B-Trees, развивались для решения различных проблем производительности, связанных с вставками, удалениями и обходами узлов.
Для простоты давайте рассмотрим базовую реализацию в псевдокоде:
1. Если дерево пустое, вставьте new_node в качестве корневого узла (очевидно!) 2. while (дерево НЕ пусто): 2а. Если (current_node пуст), вставьте его здесь и остановите; 2b. В противном случае (new_node> current_node) попробуйте вставить справа этого узла (и повторите шаг 2) 2с. В противном случае (new_node <current_node) попробуйте вставить слева этого узла (и повторите шаг 2) 2d. Остальное значение уже в дереве
В этой наивной реализации используется принцип «разделяй и властвуй». Все, что меньше текущего значения узла, идет влево, все большее — вправо, а дубликаты отклоняются. Обратите внимание, что эта стратегия сразу поддается рекурсивному решению, поскольку дерево в этом случае также может быть поддеревом.
<?php
class BinaryTree
{
...
public function insert($item) {
$node = new BinaryNode($item);
if ($this->isEmpty()) {
// special case if tree is empty
$this->root = $node;
}
else {
// insert the node somewhere in the tree starting at the root
$this->insertNode($node, $this->root);
}
}
protected function insertNode($node, &$subtree) {
if ($subtree === null) {
// insert node here if subtree is empty
$subtree = $node;
}
else {
if ($node->value > $subtree->value) {
// keep trying to insert right
$this->insertNode($node, $subtree->right);
}
else if ($node->value < $subtree->value) {
// keep trying to insert left
$this->insertNode($node, $subtree->left);
}
else {
// reject duplicates
}
}
}
}
Удаление узлов — это совсем другая история, которую мы оставим в другой раз, поскольку она потребует более глубокого рассмотрения, чем позволяет эта статья.
Прогулка по дереву
Обратите внимание, как мы начали с корневого узла и пошли по дереву, узел за узлом, чтобы найти пустой узел? Есть 4 основных стратегии, используемых для обхода дерева:
- Предварительный заказ — обработать текущий узел, а затем пересечь левое и правое поддеревья.
- по порядку (симметрично) — сначала пройти влево, обработать текущий узел, а затем перейти вправо.
- post-order — сначала пройти влево и вправо, а затем обработать текущий узел.
- level-order (breadth-first) — обработать текущий узел, затем обработать все узлы-братья, прежде чем переходить узлы на следующий уровень.
Первые три стратегии также известны как поиск по глубине или по порядку глубины, когда один начинается с корня (или с произвольного узла, обозначенного как корень) и проходит как можно дальше вниз по ветви, прежде чем вернуться назад. Каждая из этих стратегий используется в различных операционных контекстах и ситуациях, например, обход по предварительному заказу подходит для вставки узла (как в нашем примере) и клонирования поддерева (прививки). Обратный порядок по порядку обычно используется для поиска бинарных деревьев, в то время как постопорядок лучше подходит для удаления (сокращения) узлов.
Чтобы проиллюстрировать, как работает обход в порядке, давайте внесем несколько изменений в наш пример:
<?php
class BinaryNode
{
...
// perform an in-order traversal of the current node
public function dump() {
if ($this->left !== null) {
$this->left->dump();
}
var_dump($this->value);
if ($this->right !== null) {
$this->right->dump();
}
}
}
class BinaryTree
{
...
public function traverse() {
// dump the tree rooted at "root"
$this->root->dump();
}
}
Вызов метода traverse()
Вывод
Ну вот мы и в конце уже! В этой статье я познакомил вас с древовидной структурой данных и ее самой простой формой — двоичным деревом. Вы видели, как узлы вставляются в дерево и как рекурсивно обходить дерево в порядке глубины.
В следующий раз я расскажу о поиске в ширину, а также представлю некоторые новые структуры данных. Будьте на связи! До тех пор я рекомендую вам изучить другие типы деревьев и их соответствующие алгоритмы для вставки и удаления узлов.
Изображение через Fotolia