Нахождение различий в изображениях с помощью PHP

Простые различия изображений

Мы можем применять эти принципы с очень небольшим количеством кода. Давайте создадим класс для загрузки изображений, создания их растровых изображений и вычисления карты различий пикселей:

 class State
{
    private $width;
    private $height;
    private $map = [];

    public function __construct($width, $height)
    {
        $this->width = $width;
        $this->height = $height;
    }
}

Каждая карта имеет определенную ширину и высоту. Чтобы заполнить карту, нам нужно загрузить изображения в память:

 private static function createImage($path)
{
    $image = null;

    $info = getimagesize($path);
    $type = $info[2];

    if ($type == IMAGETYPE_JPEG) {
        $image = imagecreatefromjpeg($path);
    }
    if ($type == IMAGETYPE_GIF) {
        $image = imagecreatefromgif($path);
    }
    if ($type == IMAGETYPE_PNG) {
        $image = imagecreatefrompng($path);
    }

    if (!$image) {
        throw new InvalidArgumentException("image invalid");
    }

    return $image;
}

Мы можем использовать библиотеку изображений GD для чтения нескольких форматов изображений. Эта функция пытается загрузить путь к файлу, который может быть JPEG, GIF или PNG. Если ничего из этого не работает, мы можем просто поднять исключение. Почему этот метод статичен? Мы собираемся использовать его в другом статическом методе:

 public static function fromImage($path)
{
    if (!file_exists($path)) {
        throw new InvalidArgumentException("image not found");
    }

    $image = static::createImage($path);
    $width = imagesx($image);
    $height = imagesy($image);

    $map = [];

    for ($y = 0; $y < $height; $y++) {
        $map[$y] = [];

        for ($x = 0; $x < $width; $x++) {
            $color = imagecolorat($image, $x, $y);

            $map[$y][$x] = [
                "r" => ($color >> 16) & 0xFF,
                "g" => ($color >> 8) & 0xFF,
                "b" => $color & 0xFF
            ];
        }
    }

    $new = new static($width, $height);
    $new->map = $map;

    return $new;
}

Эта статическая функция позволяет нам создавать новые состояния изображения (или карты) из статического вызова State::fromImage("/path/to/image.png") Если путь не существует, мы можем вызвать другое исключение. Тогда у нас есть та же логика построения сетки изображения, которую мы видели ранее. Наконец, мы создаем новое State

Теперь давайте сделаем способ сравнить несколько изображений:

 public function withDifference(State $state, callable $method)
{
    $map = [];

    for ($y = 0; $y < $this->height; $y++) {
        $map[$y] = [];

        for ($x = 0; $x < $this->width; $x++) {
            $map[$y][$x] = $method(
                $this->map[$y][$x],
                $state->map[$y][$x]
            );
        }
    }

    return $this->cloneWith("map", $map);
}

private function cloneWith($property, $value)
{
    $clone = clone $this;
    $clone->$property = $value;

    return $clone;
}

Мы проходим каждый пиксель, каждое изображение. Мы передаем их разностной функции и присваиваем полученное значение новой карте. Наконец, мы создаем клон текущего State Это гарантирует, что мы не изменяем существующие экземпляры State

Как выглядит эта разностная функция?

 class EuclideanDistance
{
    public function __invoke(array $p, array $q)
    {
        $r = $p["r"] - $q["r"];
        $r *= $r;

        $g = $p["g"] - $q["g"];
        $g *= $g;

        $b = $p["b"] - $q["b"];
        $b *= $b;

        return sqrt($r + $g + $b);
    }
}

Оказывается, мы можем использовать классы как функции, если мы дадим им метод __invoke В этом классе мы можем поместить евклидову дистанционную логику, которую мы видели ранее. Мы можем собрать все эти части вместе вот так:

 $state1 = State::fromImage("/path/to/image1.png");
$state2 = State::fromImage("/path/to/image2.png");

$state3 = $state1->withDifference(
    $state2,
    new EuclideanDistance()
);

Этот метод отлично подходит для изображений, которые практически идентичны. Когда мы пытаемся выявить различия в очень похожих фотографиях или даже в версиях с почти одинаковыми изображениями с потерями, мы сталкиваемся со многими небольшими различиями.

Среднеквадратичное отклонение

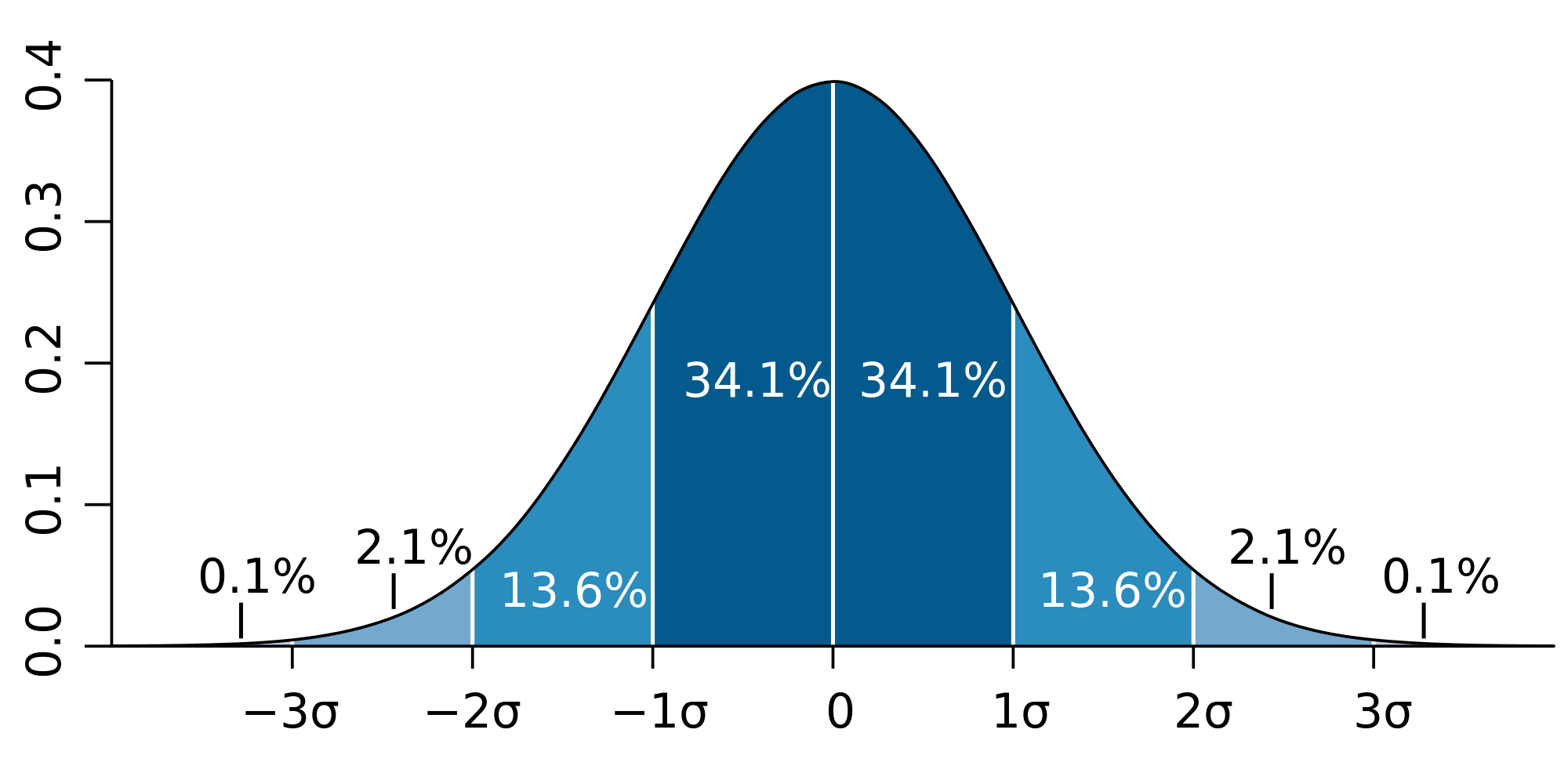
Чтобы обойти эту проблему, нам нужно убрать шум и сосредоточиться только на самой большой проблеме. Мы можем сделать это, выяснив, насколько распространены различия. Эта мера разброса чисел называется стандартным отклонением .

Изображение из Википедии

Большинство небольших различий между изображениями находятся в пределах стандартного отклонения (или темно-синяя полоса между -1σ и 1σ). Если мы устраняем все небольшие различия в стандартном отклонении, то мы должны остаться с большими различиями. Чтобы определить, какие пиксели находятся в пределах стандартного отклонения, нам нужно определить среднее значение пикселей:

 public function average()
{
    $average = 0;

    for ($y = 0; $y < $this->height; $y++) {
        for ($x = 0; $x < $this->width; $x++) {
            if (!is_numeric($this->map[$y][$x])) {
                throw new LogicException("pixel is not numeric");
            }

            $average += $this->map[$y][$x];
        }
    }

    $average /= ($this->width * $this->height);

    return $average;
}

Средние легко! Просто сложите все вместе и разделите на количество вещей, которые вы добавили вместе. В среднем две вещи их общая стоимость делится на две. В среднем 400 х 300 вещей — это их общая стоимость, разделенная на 120 000.

Обратите внимание, как мы ожидаем числовые значения во время расчета? Это означает, что сначала нам нужно сгенерировать чисто числовое состояние ( $state3EuclideanDistance

 public function standardDeviation()
{
    $standardDeviation = 0;
    $average = $this->average();

    for ($y = 0; $y < $this->height; $y++) {
        for ($x = 0; $x < $this->width; $x++) {
            if (!is_numeric($this->map[$y][$x])) {
                throw new LogicException(
                    "pixel is not numeric"
                );
            }

            $delta = $this->map[$y][$x] - $average;
            $standardDeviation += ($delta * $delta);
        }
    }

    $standardDeviation /= (($this->width * $this->height) - 1);
    $standardDeviation = sqrt($standardDeviation);

    return $standardDeviation;
}

Этот расчет немного похож на расчет расстояния, который мы делали ранее. Основная идея заключается в том, что мы определяем среднее значение всех пикселей. Затем мы выясняем, насколько далеко каждый от этого среднего, а затем вычисляем среднее для всех этих расстояний.

Мы можем применить это обратно к State

 public function withReducedStandardDeviation()
{
    $map = array_slice($this->map, 0);
    $deviation = $this->standardDeviation();

    for ($y = 0; $y < $this->height; $y++) {
        for ($x = 0; $x < $this->width; $x++) {
            if (abs($map[$y][$x]) < $deviation) {
                $map[$y][$x] = 0;
            }
        }
    }

    return $this->cloneWith("map", $map);
}

Таким образом, если различия находятся внутри полосы стандартного отклонения, мы исключаем их из нового State Результатом является более четкая картина изменений.

 public function boundary()
{
    $ax = $this->width;
    $bx = 0;
    $ay = $this->width;
    $by = 0;

    for ($y = 0; $y < $this->height; $y++) {
        for ($x = 0; $x < $this->width; $x++) {
            if ($this->map[$y][$x] > 0) {
                if ($x > $bx) {
                    $bx = $x;
                }

                if ($x < $ax) {
                    $ax = $x;
                }

                if ($y > $by) {
                    $by = $y;
                }

                if ($y < $ay) {
                    $ay = $y;
                }
            }
        }
    }

    if ($ax > $bx) {
        throw new LogicException("ax is greater than bx");
    }

    if ($ay > $by) {
        throw new LogicException("ay is greater than by");
    }

    $ax = ($ax / $this->width) * $this->width;
    $bx = ((($bx + 1) / $this->width) * $this->width) - $ax;
    $ay = ($ay / $this->height) * $this->height;
    $by = ((($by + 1) / $this->height) * $this->height) - $ay;

    return [
        "left" => $ax,
        "top" => $ay,
        "width" => $bx,
        "height" => $by
    ];
}

Последняя часть головоломки — это функция для определения границ изменений. Мы можем использовать эту функцию как способ нарисовать рамку вокруг изменений от одного изображения к другому. Коробка начинается по краям сетки и медленно перемещается внутрь, пока не достигнет изменений в сетке.

Вывод

Я начал этот эксперимент, чтобы найти различия между двумя изображениями. Видите ли, я хотел сделать скриншоты интерфейса во время автоматического тестирования и сказать, изменилось ли что-то существенное.

Евклидово расстояние, примененное к растровым изображениям, говорило мне о каждом измененном пикселе. Затем я хотел учесть небольшие изменения (например, небольшие изменения текста или цвета), поэтому я применил стандартное отклонение шума, чтобы были возможны только значительные изменения. Наконец, я мог точно определить, сколько пикселей было разным в процентах от общего количества пикселей на экране. Я мог бы сказать, был ли один скриншот в пределах 10% или 20% от изображения тестового прибора.

Возможно, вам это нужно для чего-то совершенно другого. Возможно, у вас есть идеи, как это можно улучшить. Дайте нам знать об этом в комментариях!