Обобщения позволяют вам объявить переменную, которая при исполнении может быть назначена набору типов, определенных нами.
В Swift массив может содержать данные любого типа. Если нам нужен массив целых чисел, строк или чисел с плавающей точкой, мы можем создать его с помощью стандартной библиотеки Swift. Тип, который должен содержать массив, определяется при его объявлении. Массивы являются распространенным примером использования обобщений. Если бы вы реализовали свою собственную коллекцию, вы бы наверняка захотели использовать дженерики.
Давайте рассмотрим дженерики и какие замечательные вещи они позволяют нам делать.
1. Общие функции
Мы начинаем с создания простой универсальной функции. Наша цель — создать функцию для проверки того, что любые два объекта имеют одинаковый тип. Если они одного типа, тогда мы сделаем значение второго объекта равным значению первого объекта. Если они не одного типа, мы напечатаем «не одного типа». Вот попытка реализации такой функции в Swift.
|
1
2
3
4
5
6
7
8
9
|
func sameType (one: Int, inout two: Int) -> Void {
// This will always be true
if(one.dynamicType == two.dynamicType) {
two = one
}
else {
print(«not same type»)
}
}
|
В мире без дженериков мы сталкиваемся с серьезной проблемой. В определении функции нам нужно указать тип каждого аргумента. В результате, если мы хотим, чтобы наша функция работала со всеми возможными типами, нам нужно было бы написать определение нашей функции с различными параметрами для каждой возможной комбинации типов. Это не жизнеспособный вариант.
|
1
2
3
4
5
6
7
8
9
|
func sameType (one: Int, inout two: String) -> Void {
// This would always be false
if(one.dynamicType == two.dynamicType) {
two = one
}
else {
print(«not same type»)
}
}
|
Мы можем избежать этой проблемы, используя дженерики. Посмотрите на следующий пример, в котором мы используем дженерики.
|
1
2
3
4
5
6
7
8
|
func sameType<T,E>(one: T, inout two: E) -> Void {
if(one.dynamicType == two.dynamicType) {
two = one
}
else {
print(«not same type»)
}
}
|
Здесь мы видим синтаксис использования дженериков. Общие типы обозначены символами T и E Типы указываются путем помещения <T,E> в определение нашей функции после имени функции. Думайте о T и E как о заполнителях для любого типа, с которым мы используем нашу функцию.
Однако есть серьезная проблема с этой функцией. Это не скомпилируется. Компилятор сгенерирует ошибку, указывающую, что T не конвертируется в E Обобщения предполагают, что, поскольку T и E имеют разные метки, они также будут разных типов. Это хорошо, мы все еще можем достичь нашей цели с помощью двух определений нашей функции.
|
1
2
3
4
5
6
7
|
func sameType<T,E>(one: T, inout two: E) -> Void {
print(«not same type»)
}
func sameType<T>(one: T, inout two: T) -> Void {
two = one
}
|
Есть два случая для аргументов нашей функции:
- Если они одного типа, вызывается вторая реализация. Значение
twoзатем присваиваетсяone. - Если они относятся к разным типам, вызывается первая реализация, и на консоль выводится строка «не того же типа».
Мы сократили наши определения функций с потенциально бесконечного числа комбинаций типов аргументов до двух. Наша функция теперь работает с любой комбинацией типов в качестве аргументов.
|
01
02
03
04
05
06
07
08
09
10
|
var s = «apple»
var p = 1
sameType(2,two: &p)
print(p)
sameType(«apple», two: &p)
// Output:
1
«not same type»
|
Общее программирование также может применяться к классам и структурам. Давайте посмотрим, как это работает.
2. Общие классы и структуры
Рассмотрим ситуацию, когда мы хотели бы создать наш собственный тип данных, двоичное дерево. Если мы используем традиционный подход, в котором мы не используем дженерики, то мы будем создавать двоичное дерево, которое может содержать только один тип данных. К счастью, у нас есть дженерики.
Бинарное дерево состоит из узлов, которые имеют:
- два ребенка или ветви, которые являются другими узлами
- часть данных, которая является общим элементом
- родительский узел, который обычно не является ссылкой на узел
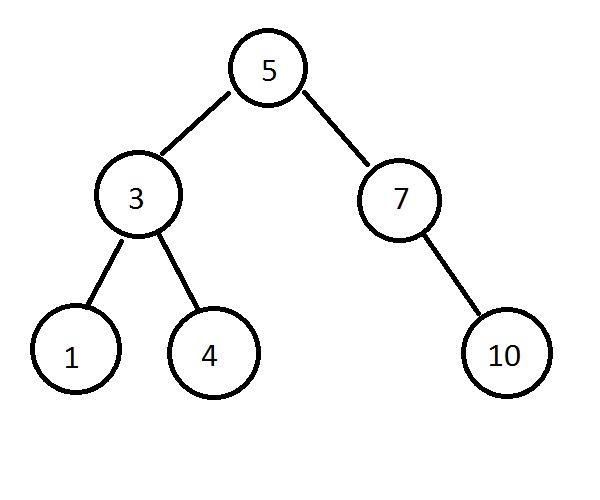
Каждое двоичное дерево имеет головной узел, у которого нет родителей. Двое детей обычно различаются как левый и правый узлы.
Любые данные в левом дочернем элементе должны быть меньше, чем родительский узел. Любые данные в правом дочернем элементе должны быть больше, чем родительский узел.
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
|
class BTree <T: Comparable> {
var data: T?
var left: BTree<T>?
var right: BTree<T>?
func insert(newData: T) {
if (self.data > newData) {
// Insert into left subtree
}
else if (self.data < newData) {
// Insert into right subtree
}
else if (self.data == nil) {
self.data = newData
return
}
}
}
|
Объявление класса BTree также объявляет универсальный T , который ограничен протоколом Comparable . Мы обсудим протоколы и ограничения немного.
Элемент данных нашего дерева определен как тип T Любой вставленный элемент также должен иметь тип T как указано в объявлении метода insert(_:) . Для универсального класса тип указывается при объявлении объекта.
|
1
|
var tree: BTree<int>
|
В этом примере мы создаем двоичное дерево целых чисел. Создать общий класс довольно просто. Все, что нам нужно сделать, это включить общее в объявление и при необходимости ссылаться на него в теле.
3. Протоколы и ограничения
Во многих ситуациях нам приходится манипулировать массивами для достижения программной цели. Это может быть сортировка, поиск и т. Д. Мы рассмотрим, как генерики могут помочь нам в поиске.
Основная причина, по которой мы используем универсальную функцию для поиска, заключается в том, что мы хотим иметь возможность поиска в массиве независимо от того, какой тип объектов он содержит.
|
01
02
03
04
05
06
07
08
09
10
|
func find <T> (array: [T], item : T) ->Int?
var index = 0
while(index < array.count) {
if(item == array[index]) {
return index
}
index++
}
return nil;
}
|
В приведенном выше примере функция find(array:item:) принимает массив универсального типа T и ищет его на item соответствия item также типа T
Хотя есть проблема. Если вы попытаетесь скомпилировать приведенный выше пример, компилятор выдаст еще одну ошибку. Компилятор говорит нам, что бинарный оператор == нельзя применять к двум T операндам. Причина очевидна, если вы думаете об этом. Мы не можем гарантировать, что универсальный тип T поддерживает оператор == . К счастью, Свифт покрыл это. Посмотрите на обновленный пример ниже.
|
01
02
03
04
05
06
07
08
09
10
|
func find <T: Equatable> (array: [T], item : T) ->Int?
var index = 0
while(index < array.count) {
if(item == array[index]) {
return index
}
index++
}
return nil;
}
|
Если мы укажем, что универсальный тип должен соответствовать протоколу Equatable , то компилятор дает нам пропуск. Другими словами, мы применяем ограничение на то, что типы T могут представлять. Чтобы добавить ограничение к универсальному, вы должны перечислить протоколы в угловых скобках.
Но что это значит для чего-то, чтобы быть Equatable ? Это просто означает, что он поддерживает оператор сравнения == .
Equatable — не единственный протокол, который мы можем использовать. Swift имеет другие протоколы, такие как Hashable и Comparable . Мы видели Comparable ранее в примере двоичного дерева. Если тип соответствует Comparable протоколу, это означает, что операторы < и > поддерживаются. Я надеюсь, что ясно, что вы можете использовать любой протокол, который вам нравится, и применять его в качестве ограничения.
4. Определение протоколов
Давайте рассмотрим пример игры, чтобы продемонстрировать ограничения и протоколы в действии. В любой игре у нас будет ряд объектов, которые нужно со временем обновлять. Это обновление может касаться положения объекта, состояния здоровья и т. Д. А пока давайте воспользуемся примером состояния объекта.
В нашей реализации игры у нас было много различных объектов со здоровьем, которые могли бы быть врагами, союзниками, нейтральными и т. Д. Они не все были бы того же класса, поскольку все наши различные объекты могли бы иметь разные функции.
Мы бы хотели создать функцию с именем check(_:) проверить состояние данного объекта и обновить его текущее состояние. В зависимости от состояния объекта мы можем вносить изменения в его здоровье. Мы хотим, чтобы эта функция работала со всеми объектами независимо от их типа. Это означает, что нам нужно сделать check(_:) универсальная функция. Таким образом, мы можем перебирать различные объекты и вызывать check(_:) для каждого объекта.
Все эти объекты должны иметь переменную для представления их здоровья и функцию для изменения их живого статуса. Давайте объявим протокол для этого и назовем его Healthy .
|
1
2
3
4
|
protocol Healthy {
mutating func setAlive(status: Bool)
var health: Int { get }
}
|
Протокол определяет, какие свойства и методы должен реализовать тип, соответствующий протоколу. Например, протокол требует, чтобы любой тип, соответствующий протоколу Healthy , реализовывал мутирующую setAlive(_:) . Протокол также требует свойство с именем health .
Давайте теперь вернемся к функции check(_:) мы объявили ранее. Мы указываем в объявлении с ограничением, что тип T должен соответствовать Healthy протоколу.
|
1
2
3
4
5
|
func check<T:Healthy>(inout object: T) {
if (object.health <= 0) {
object.setAlive(false)
}
}
|
Мы проверяем свойство health объекта. Если оно меньше или равно нулю, мы вызываем setAlive(_:) для объекта, передавая false . Поскольку T требуется для соответствия протоколу Healthy , мы знаем, что setAlive(_:) может вызываться для любого объекта, который передается функции check(_:) .
5. Связанные типы
Если вы хотите дополнительно контролировать свои протоколы, вы можете использовать связанные типы. Давайте вернемся к примеру двоичного дерева. Мы хотели бы создать функцию для выполнения операций над двоичным деревом. Нам нужен какой-то способ убедиться, что входной аргумент удовлетворяет тому, что мы определяем как двоичное дерево. Чтобы решить эту проблему, мы можем создать протокол BinaryTree .
|
1
2
3
4
5
6
|
protocol BinaryTree {
typealias dataType
mutating func insert(data: dataType)
func index(i: Int) -> dataType
var data: dataType { get }
}
|
При этом используется связанный тип typealias dataType . dataType похож на универсальный. T из ранее, ведет себя аналогично dataType . Мы указываем, что двоичное дерево должно реализовывать функции insert(_:) и index(_:) . insert(_:) принимает один аргумент типа dataType . index(_:) возвращает объект dataType . Мы также указываем, что двоичное дерево должно иметь data свойства, dataType тип dataType .
Благодаря нашему связанному типу мы знаем, что наше двоичное дерево будет согласованным. Можно предположить, что тип, переданный для insert(_:) , заданный index(_:) и содержащийся в data одинаков для каждого. Если бы типы не были одинаковыми, мы столкнулись бы с проблемами.
6. Где пункт
Swift также позволяет использовать предложения where с обобщениями. Посмотрим, как это работает. Есть две вещи, где пункты позволяют нам достигать с обобщениями:
- Мы можем обеспечить, чтобы связанные типы или переменные в протоколе были одного типа.
- Мы можем назначить протокол для связанного типа.
Чтобы показать это в действии, давайте реализуем функцию для управления бинарными деревьями. Цель состоит в том, чтобы найти максимальное значение между двумя двоичными деревьями.
Для простоты мы добавим функцию к протоколу BinaryTree , которая называется inorder() . In-order — один из трех популярных типов обхода в глубину . Это порядок узлов дерева, который перемещается рекурсивно, левое поддерево, текущий узел, правое поддерево.
|
1
2
3
4
5
6
7
8
|
protocol BinaryTree {
typealias dataType
mutating func insert(data: dataType)
func index(i: Int) -> dataType
var data: dataType { get }
// NEW
func inorder() -> [dataType]
}
|
Мы ожидаем, что функция inorder() вернет массив объектов связанного типа. Мы также реализуем функцию twoMax(treeOne:treeTwo:) , которая принимает два двоичных дерева.
|
01
02
03
04
05
06
07
08
09
10
|
func twoMax<B: BinaryTree, T: BinaryTree where B.dataType == T.dataType, B.dataType: Comparable, T.dataType: Comparable> (inout treeOne: B, inout treeTwo: T) -> B.dataType {
var inorderOne = treeOne.inorder()
var inorderTwo = treeTwo.inorder()
if (inorderOne[inorderOne.count] > inorderTwo[inorderTwo.count]) {
return inorderOne[inorderOne.count]
} else {
return inorderTwo[inorderTwo.count]
}
}
|
Наша декларация довольно длинная из-за предложения where . Первое требование B.dataType == T.dataType гласит, что связанные типы двух двоичных деревьев должны быть одинаковыми. Это означает, что их объекты data должны быть одного типа.
Второй набор требований, B.dataType: Comparable, T.dataType: Comparable , B.dataType: Comparable, T.dataType: Comparable , указывает, что связанные типы обоих должны соответствовать протоколу Comparable . Таким образом, мы можем проверить, какое максимальное значение при сравнении.
Интересно, что из-за природы двоичного дерева мы знаем, что последний элемент порядка будет максимальным элементом в этом дереве. Это потому, что в двоичном дереве самый правый узел является самым большим. Нам нужно только взглянуть на эти два элемента, чтобы определить максимальное значение.
У нас есть три случая:
- Если tree one содержит максимальное значение, то последний элемент его inorder будет наибольшим, и мы вернем его в первом операторе
if. - Если дерево два содержит максимальное значение, то последний элемент его inorder будет наибольшим, и мы вернем его в предложении
elseпервого оператораif. - Если их максимумы равны, то мы возвращаем последний элемент в дереве второго порядка, который по-прежнему является максимумом для обоих.
Вывод
В этом уроке мы сосредоточились на дженериках в Swift. Мы узнали о значении дженериков и изучили, как использовать дженерики в функциях, классах и структурах. Мы также использовали обобщения в протоколах и исследовали связанные типы и предложения where.
При хорошем понимании обобщений вы можете создавать более универсальный код и лучше справляться с трудными проблемами кодирования.