Тайна не раскрыта.
При последнем рассмотрении структура Apache Ant выглядела странно.
Что-то не совсем подходит.
Проблема касается кортежей функциональных зависимостей : Ant может похвастаться шокирующими 504776 маленькими болтунами.
То есть, если вы выстроите все функции Ant, от которых нет зависимостей, и попытаетесь отследить все пути исходных кодов от них — по сути, перечисляя все транзитивные зависимости системы — вы найдете полмиллиона различных цепочек функций.
Полмиллиона.
Для сравнения, у JUnit 2700 кортежей зависимостей. Конечно, Ant растягивается в три раза больше, чем JUnit, Ant имеет 4500 функций, JUnit, 1300. Кроме того, взаимосвязь между количеством функций и числом наборов зависимостей функций является сложной, поэтому можно ожидать, что в три раза больше функций может скажем, в пять раз больше кортежей зависимостей, скажем, в десять раз. Но увеличить это число на два порядка?
Странность лежит здесь.
И это не просто академическое любопытство. Каждый раз, когда программист обновляет функцию, существует ненулевая вероятность того, что такое обновление вызовет изменения волнового эффекта для других зависимых функций, что приведет к увеличению потенциальных затрат. Странно растущее число кортежей зависимостей, безусловно, не уменьшает такие потенциальные затраты. Корпоративная ответственность требует объяснения.
Итак, давайте перетащим труп Муравья в морг и предадимся безвозмездному монтажу врачей, выглядящих серьезно, нарезающих скальпели и окровавленные органы, взвешиваемые на весах из нержавеющей стали, и все до болезненно бедренного саундтрека.
Amplification.
На самом деле, даже прежде, чем мы рассмотрим Ant, давайте быстро взглянем на некоторые особенности кортежей зависимостей. Рассмотрим одноклассную систему, включающую функции, показанные на рисунке 1.
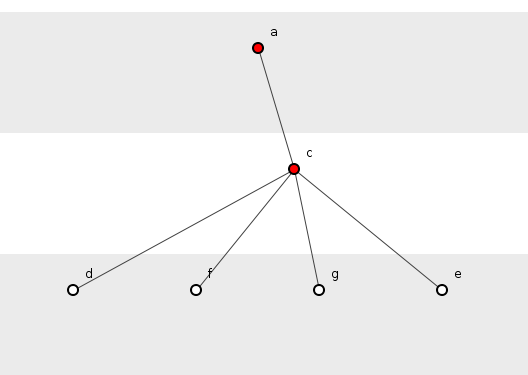
Рисунок 1: Простая система.
На рисунке 1, мы имеем четыре кортежей зависимостей: { a(), c(), d()}, { a(), c(), f()}, { a(), c(), g()} и { a(), c(), e()}, все расположены в благородном и классическом Санберст узора.
Зачем исследовать столь тривиальную систему, прежде чем углубляться в монстра? Что ж, вырезание вручную полумиллиона кортежей зависимости из безупречного цифрового мрамора звучит чрезмерно долго. Что, если какой-то комбинаторный эффект скрывается из поля зрения? Что если вместо того, чтобы программист явно создавал эти кортежи зависимостей, некоторые конфигурации функций увеличивали количество кортежей зависимостей сверх тех, которые были «намеренно» созданы?
Это конфигурации, которые мы ищем, в которых добавление одной зависимости дает более одного дополнительного кортежа зависимости. Например, на рисунке 1, что произойдет, если мы добавим еще одну функцию h(), вызываемую c()? Это показано на рисунке 2.
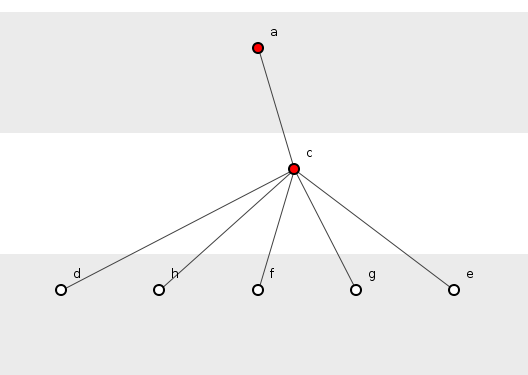
Рисунок 2: Вызвана дополнительная функция.
Рисунок 2 теперь дает пять кортежи зависимостей: { a(), c(), d()}, { a(), c(), h()}, { a(), c(), f()}, { a(), c(), g()} и { a(), c(), e()}. Таким образом, добавив еще одну зависимость, мы добавили еще один кортеж зависимости. Усиление здесь не произошло.
Однако рассмотрим, добавим ли мы новую функцию b(), которая c()скорее вызывает, чем вызывает ее.
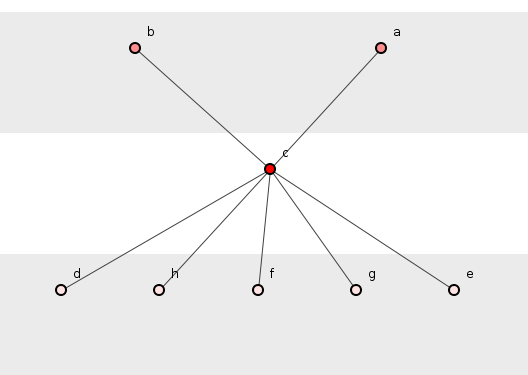
Рисунок 3: Новая функция создания усиления.
Внезапно на рисунке 3 показаны десять кортежей зависимостей, в два раза больше, чем на рисунке 2, хотя мы добавили только одну новую функцию и одну новую зависимость. Хотя именно тот эффект, к которому мы стремились, это поражает, теперь безжизненно лежащий перед нами, как восторг. Дополнительные пять кортежей происходят от вызова функции, которая в свою очередь имеет пять зависимостей. Разве это не очевидно?
Однако тонкость движется под поверхностью. Поскольку программист должен был создать новую функцию, чтобы вызвать усиление и создать — на то, что мы теперь видим как ключевой камень на рисунке 3, c()— новую зависимость. Оба влекут за собой обдуманность и недвусмысленность, которую может заметить настороженный программист, если бы этот программист интересовался такими вопросами.
Все же некоторые случаи работают на более коварных уровнях, возможно, наиболее пагубными являются те, которые связаны со скрытым преступным миром круговых зависимостей.
Вы можете подумать, что простое добавление зависимости от d()back к b()вызовет все виды циклических махинаций, но это не так. Spoiklin Soice , производитель этих диаграмм, должен, как и все такие анализаторы зависимостей, защищать от бесконечных циклов, где возникают циклические зависимости, и поэтому зависимость от функции, которая уже находится в анализируемом кортеже зависимостей, приводит к прекращению анализа, помечая этот кортеж как циклический.
«Уловка» состоит в том, чтобы включить зависимость от концентратора, которая не приходит непосредственно от двух родительских функций, a()или b(), и это, увы, происходит слишком часто.
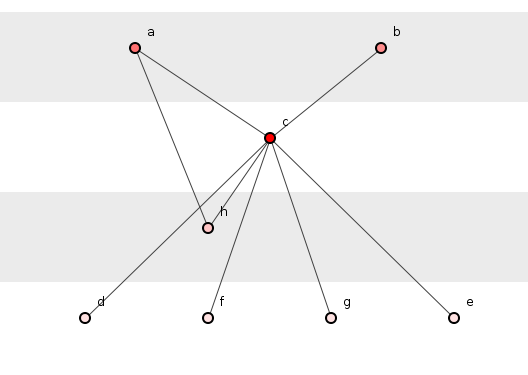
Рисунок 4: Предциклическая ловушка установлена.
На рисунке 4 показаны те же функции, что и на рисунке 3, только с добавленной дополнительной зависимостью от a()on h(). Это не вызывает усиления и создает только один дополнительный кортеж зависимости: где на рисунке 3 было десять, на рисунке 4 — одиннадцать. На следующем рисунке, однако, мы увидим эффект от введения нашей круговой зависимости между h()хабом и c().
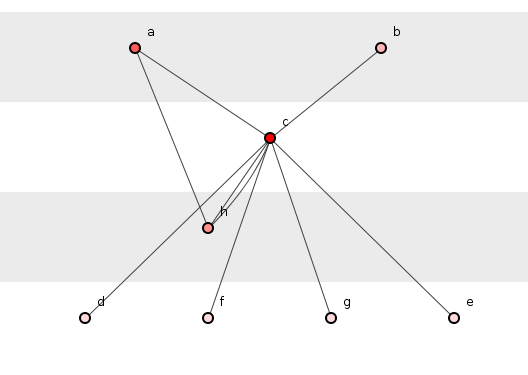
Рисунок 5: Круговое усиление.
Рисунок 5 демонстрирует усиление, вызванное новой циклической зависимостью. Там, где на рисунке 4 имеется одиннадцать кортежей зависимостей, добавление еще одной зависимости — и никаких новых функций — на рисунке 5 теперь создает пятнадцать кортежей зависимостей. (Примечание: не шестнадцать кортежей зависимостей. Почему?)
Все это, заметьте, в тривиальной системе из восьми функций, которая, несмотря на свой размер, предлагает нетривиальную задачу для прогнозирования усиления в кортеже зависимостей. Это явление, опять же, касается реальной проблемы управления затратами в условиях геометрически увеличенных векторов волновых эффектов в реальных программных продуктах. Представьте себе, насколько более болезненной становится эта проблема в системе из тысячи функций или четырех тысяч.
Для остроумия …
Еще раз в муравья.
Несмотря на невероятную сложность муравьих кортежей пятисот четырех тысяч семьсот семидесяти шести, найти место для прохождения лабиринта безумия оказывается не проблема. Одна функция торчит.
Эта функция Path.list()и через нее каскадные кортежи зависимостей 356440 составляют более половины нагрузки всей системы. Здесь мы обнаруживаем наш центр, нашу брюшную тиф Мэри.
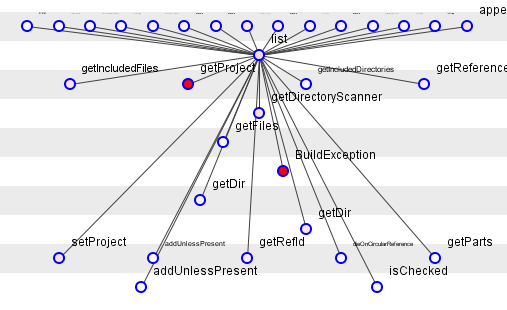
Рисунок 6: Path.list ()
Вы можете не думать, просто взглянув на list()рисунок 6, что это был такой хулиган. Да, от этого зависит шестнадцать функций, и еще семнадцать других, так что компания не стесняется, но вряд ли это выделит для особого отношения.
И это не то, что вы могли бы назвать «Смотрителем».
Взгляните на себя, хотя он показан здесь полностью для полноты; не пытайтесь распутать это:
/**
* Returns all path elements defined by this and nested path objects.
* @return list of path elements.
*/
public String[] list() {
if (!isChecked()) {
// make sure we don't have a circular reference here
Stack stk = new Stack();
stk.push(this);
dieOnCircularReference(stk, getProject());
}
Vector result = new Vector(2 * elements.size());
for (int i = 0; i < elements.size(); i++) {
Object o = elements.elementAt(i);
if (o instanceof Reference) {
Reference r = (Reference) o;
o = r.getReferencedObject(getProject());
// we only support references to paths right now
if (!(o instanceof Path)) {
String msg = r.getRefId() + " doesn\'t denote a path " + o;
throw new BuildException(msg);
}
}
if (o instanceof String) {
// obtained via append
addUnlessPresent(result, (String) o);
} else if (o instanceof PathElement) {
String[] parts = ((PathElement) o).getParts();
if (parts == null) {
throw new BuildException("You must either set location or"
+ " path on ");
}
for (int j = 0; j < parts.length; j++) {
addUnlessPresent(result, parts[j]);
}
} else if (o instanceof Path) {
Path p = (Path) o;
if (p.getProject() == null) {
p.setProject(getProject());
}
String[] parts = p.list();
for (int j = 0; j < parts.length; j++) {
addUnlessPresent(result, parts[j]);
}
} else if (o instanceof DirSet) {
DirSet dset = (DirSet) o;
DirectoryScanner ds = dset.getDirectoryScanner(getProject());
String[] s = ds.getIncludedDirectories();
File dir = dset.getDir(getProject());
addUnlessPresent(result, dir, s);
} else if (o instanceof FileSet) {
FileSet fs = (FileSet) o;
DirectoryScanner ds = fs.getDirectoryScanner(getProject());
String[] s = ds.getIncludedFiles();
File dir = fs.getDir(getProject());
addUnlessPresent(result, dir, s);
} else if (o instanceof FileList) {
FileList fl = (FileList) o;
String[] s = fl.getFiles(getProject());
File dir = fl.getDir(getProject());
addUnlessPresent(result, dir, s);
}
}
String[] res = new String[result.size()];
result.copyInto(res);
return res;
}
Опять же: противный, хотя и не явно 356440-кортеж зависимостей.
Но подождите, подождите, подождите: мы можем решить проблему, если немного обмануть. Давайте притворимся, что list()функция выглядит не так, как выше, но сводится к следующему:
/**
* Returns all path elements defined by this and nested path objects.
* @return list of path elements.
*/
public String[] list() {
Object o = elements.elementAt(0);
DirSet dset = (DirSet) o;
DirectoryScanner ds = dset.getDirectoryScanner(getProject());
return null;
}
Да, эта функция теперь не имеет смысла, даже возвращая смертельный ноль, который наверняка приведет к падению муравья. Это, однако, является не анализом реализации пользовательского опыта Ant, а его структурой и структурным анализом, которые все время вызывают странные трюки, в данном случае, выполняя локальное структурное сокращение, будь прокляты последствия во время выполнения. С мультяшным рефакторингом, приведенным выше, число кортежей зависимости Ant падает с 504776 до 450259.
Вы можете подумать, что впечатляет то, что удаление нескольких десятков строк кода может привести к сокращению 50000 кортежей зависимостей, но зверь остается: четыреста пятьдесят тысяч кортежей зависимостей все еще ткут непостижимый мат. Теперь рассмотрим, что происходит сейчас, если удалить эту строку:
DirectoryScanner ds = dset.getDirectoryScanner(getProject());
Количество кортежей зависимостей резко упало до 149014.
Эта единственная строка кода генерирует триста тысяч кортежей зависимостей, что, безусловно, является лучшим примером усиления с тех пор, как вселенная прыгающего ребенка закончила надуваться.
И почему? Потому что getDirectoryScanner()имеет транзитивную зависимость от list(): они находятся в одном кортеже зависимостей, поэтому, однажды list()вызывая getDirectoryScanner()длинный извилистый контур, завершает соединительную цепочку за цепочкой усиливающих функций, возвращаясь к себе, бездумно каскадируя.
На каких конкретных функциях между getDirectoryScanner()и list()эти усиления происходят? Кто может сказать? Ответ требует еще более тщательного отслеживания, возможно, тянет связки часами, чтобы увидеть, какие подергивающиеся органы в конечном итоге связаны.
И в этом заключается суть: плохо структурированные системы затрудняют анализ зависимостей, и это напрямую приводит к трудностям в прогнозировании затрат на обновление.
Являются ли плохо структурированные системы всегда более дорогостоящими для обновления, чем хорошо структурированные системы? Конечно, нет, но стоимость обновления плохо структурированных систем всегда сложнее предсказать.
Ant оказывается в этой ситуации, потому что он нарушил как минимум два принципа хорошей структуры : у него слишком много циклических зависимостей и он слишком глубокий .
Но поиск лекарства никогда не был частью этого анализа: мы хотели найти источник болезни, и даже в этой задаче окончательная идентификация остается труднодостижимой. С некоторой нарезкой и бурением и осторожной спекуляцией, однако, мы, по крайней мере , в пределах дома -hunch.
(Обратите внимание, что обсуждаемая здесь версия Ant — 1.6.0, и в более поздней версии list()она подверглась рефакторингу, но даже эта версия имеет такое же огромное количество кортежей зависимостей, поэтому любой рефакторинг просто перемещал усилители в другое место.)
Резюме.
Ant остается отличным программным обеспечением, обеспечивающим фантастическую ценность для бизнеса во всем мире. Он по-прежнему заслуживает своего места одним из самых популярных строительных инструментов дня.
Этот анализ, однако, касался не Ant-инструмента, ориентированного на пользователя, а Ant-структуры, и пытался объяснить, почему Ant содержит несколько кортежей зависимостей, которые значительно отличаются от его размера.
Фото кредитная атрибуция.
CC Image PICT0039.JPG предоставлено the_lost_drones на Flickr.
