Путешествует хоть логика.
Посмотри на это.
void greet() {
String hello = getHello();
String subject = getSubject(1);
showGreeting(hello, subject);
}
private String getHello() {
return "Hello";
}
private String getSubject(int i) {
if (i == 0) {
return "Fred";
}
if (i == 1) {
return "world";
}
return "everybody";
}
private void showGreeting(String hail, String subject) {
System.out.println(hail + ", " + subject + ".");
}
Утомительный, смехотворно перегруженный Java-код, но разве это теорема?
Суд по терминологии.
Первый: что такое теорема?
Хорошо, старая вики говорит нам, что «Логика … рассматривает теоремы как утверждения (называемые формулами или правильно сформированными формулами) формального языка. Должен быть предоставлен набор правил вывода, также называемых правилами преобразования или правилами вывода. Эти правила вывода точно указывают, когда формула может быть получена из набора предпосылок «. И далее: «Первоначально принятые формулы в выводе называются его аксиомами и являются основой, на которой основывается теорема».
То, что «… получено из ряда предпосылок», подразумевает, что теоремы могут быть доказаны там, где, опять же, вики «доказательство является дедуктивным аргументом для математического утверждения», и далее « Дедуктивное рассуждение связывает предпосылки с выводами. все предпосылки верны, условия понятны, и правила дедуктивной логики соблюдаются, тогда сделанный вывод обязательно верен ».
Что же это за любопытный зверь, дедуктивное мышление?
Дедуктивное мышление.
При первом изучении дедукции студенты обычно сталкиваются с силлогизмом, в котором утверждение следует из двух других:
- Все люди смертны.
- Аристотель — мужчина.
- Следовательно, Аристотель смертен.
Этот силлогизм — « Смертный Аристотель », силлогизм — имеет две предпосылки: первое, что все люди смертны, и второе, что Аристотель — человек. Затем он предлагает сделать вывод из этих предпосылок, а именно, что Аристотель смертен. Принимая во внимание то, что большинство считает, что «все люди смертны» и «Аристотель — человек» в качестве изначально принятых утверждений (или, на языке определения Вики, формул), а также учитывая, что Мортал Аристотель использует вычет для производства В заключение, силлогизм, по-видимому, отвечает всем критериям теоремы. Правда, это может быть просто частичка теоремы, гомеопатическая настойка теоремы, но, тем не менее, теорема такова.
Здесь исследование того, может ли исходный код быть теоремой, может выиграть от временной инверсии: может ли эта теорема Мортал Аристотель быть записана как исходный код? И конечно может.
class Aristotle extends Man {
.
.
.
}
boolean isMortal(Object object) {
return object instanceof Man;
}
System.out.println(isMortal(new Aristotle()));
Этот код, безусловно, выглядит со стороны. У него есть Человек, Аристотель и даже что-то вроде вычета смертности. Это безобразие instanceofне должно отвлекать ученика от того, как метод воплощает дедукцию, выводя свойства вещей из свойств других вещей. Форма, которую принимает код — тонкости вывода свойств — вряд ли имеет значение; любое количество альтернатив тоже подойдет. Например:
boolean isMortal(Creature creature) {
return creature.hasProperty(Property.Man);
}
Или метод в предлагаемом Manклассе:
@Override
boolean isMortal() {
return hasProperty(Property.MORTAL);
}
Или даже:
@Override
boolean isMortal() {
return true;
}
Основной вычет остается.
Но помимо демонстрации определенного произвола реализации, эти примеры не могут кристаллизовать основной вывод. Какое устройство могло бы придумать человечество, чтобы сделать резкий вывод из такой белой мраморной предпосылки?
Ответ: человечество в глубине древности создало устройство редкой ценности. Это устройство дает нам основание рационального мышления, непоколебимо глубокое, звучно названное «Modus ponens».
Модус поненс.
Modus ponens , одно из немногих формальных правил дедукции, позволяет делать выводы из других утверждений. Он достаточно силен, чтобы взвесить всю систему логики на широкие плечи, и находит выражение в форме:
- Утверждение P подразумевает утверждение Q.
- Утверждение P верно.
- Следовательно, утверждение Q верно.
Эти несколько строк раскрывают сущность дедуктивной логики: первая предпосылка — условная — объединяется со второй предпосылкой, чтобы логически вывести заключение. Более того, условная предпосылка разлагается на антецедент P и последующее Q. Во второй предпосылке просто утверждается P, антецедент условного, в то время как заключение выводит истинность Q, как условного следствия.
Обе предпосылки могут быть как истинными, так и ложными, если modus ponens гарантирует сохранение правды. Если оба предположения верны, то заключение должно быть верным. Таким ревом Модус Поненс.
В удивительно краткой символике логики, где → обозначает логическое значение, а ∴ обозначает «поэтому», modus ponens использует следующую приятную стенографию.
P → Q, P ∴ Q
Это читается как: «Учитывая, что P подразумевает, что Q истинно, а учитывая, что P истинно, следовательно, Q должно быть истинно».
(Логика, как правило, опускает «истинно», соглашаясь на: «Учитывая P подразумевает Q и данный P, поэтому Q.». Программисты отмечают здесь свою собственную историю, обычно интерпретируя условное выражение как: ifP thenQ.)
Смертный Аристотель, таким образом, проявляет себя как просто modus ponens в симпатичном парике, и, учитывая, что, как мы видели выше, Mortal Aristotle является одной из простейших форм теоремы, поэтому каждый modus ponens тоже носит тег «Теорема», имя , Так можем ли мы извлечь из Смертного Аристотеля три определяющих элемента modus ponens? Ответ на этот вопрос приводит нас к основному утверждению: программный метод выражает условную предпосылку modus ponens.
class Aristotle extends Man {
.
.
.
}
boolean isMortal(Object object) {
return object instanceof Man;
}
System.out.println(isMortal(new Aristotle()));
В этом случае условная предпосылка гласит: объект, являющийся экземпляром класса Man, подразумевает его смертность. Или в более дружественной для программиста формеif-then : если объект является экземпляром Manкласса, тогда этот объект смертелен . Фактический механизм реализации этого условия включает семантику имени метода и каждого последнего фрагмента его аргументов, тела и возвращаемого значения.
Сама структура класса охватывает вторую предпосылку, хотя, как видно выше, такая специфика не ограничивает общности. В Aristotleпроисходящем классе из Manкласса , таким образом , утверждает: объект является экземпляром класса Man .Aristotle
Последняя часть, заключение, с любопытством искажается, когда проецируется с языка логики на компьютерный код, потому что Java моделирует этот конкретный вывод из предпосылок и, следовательно, достижение выводов, как вызов метода. Таким образом, вывод является результатом выполнения: оцените isMortal()метод с помощью Aristotleобъекта .
Таким образом, со структурой модус поненс , отображенным на Смертельный Аристотелем исходный код, внимание может теперь перейти от Смертельной Аристотеля по отношению к попытке подобного отображения в исходном коде , с которым открыт этот пост.
getHello()Теорема.
getHello()Метод принимает этап первым, не принимая никаких аргументов и всегда возвращаются одинаковое значение строки, "Hello".
private String getHello() {
return "Hello";
}
Может ли это быть теорема? Выражает ли это условную предпосылку modus ponens? И если да, каковы его предпосылки и заключение?
В этом случае условная посылка кажется странным безусловна, а именно , что, независимо от всего остального, метод возвращает, "Hello". Однако этот метод принципиально отличается от исходного кода Mortal Aristotle тем, что isMortal()служит примером предиката, то есть он оценивает на основе своих аргументов значение true или false и ничего больше. Предикаты разделяют эту истинную / ложную дихотомию с утверждениями, оба являются логическими сущностями, над которыми счастливо действует modus ponens, ни один из которых никогда не оценивает что-либо столь же неуправляемое как String.
К счастью, исследования в логике исходного кода проводятся параллельно с самим исходным кодом, делая заявления о том, что делает исходный код. В этом случае может быть сделано утверждение, что метод оценивает "Hello"при любых обстоятельствах утверждение, которое оценивается как истинное или ложное. Логики фиксируют неизменность этого значения с помощью фразы: если true, то оценивается как"Hello" . Метод выражает эту неизменность, не принимая аргументов: он будет возвращать "Hello"строку,, при вызове, каждый раз.
Вторая предпосылка метода выражается в упущении, так как для его установления не требуются ни данные, ни логическая структура. Напомним, что вторая предпосылка просто ifсоответствует условному утверждению, которое, как было установлено выше, является константой, истинной. Поскольку true остается всегда и неизменно истинным, метод, не принимающий аргументов, эффективно отображает вторую предпосылку, просто: true .
Аналогичным образом, система устанавливает достоверность утверждения обеих предпосылок для получения заключения посредством вызова метода без аргументов. Отсюда вывод: оценивается"Hello" и, таким образом, метод в целом принимает следующую логическую форму.
getHello()= верно → оценивает до "Hello", верно ∴ оценивает до"Hello"
Мы интерпретируем это как: учитывая, что истина подразумевает, что getHello()оценивает "Hello"и, учитывая истину, затем getHello()оценивает "Hello". Ниже приведен силлогистический формат.
getHello()знак равно
- true → оценивается как
"Hello" - правда
- ∴ оценивает
"Hello"
Теперь мы можем рассуждать об этом методе, анализируя, сохраняет ли он истину, задавая вопрос: дано ли значение true для вызова этого метода "Hello"? Или немного уменьшено: верно, getHello()== оценивается как "Hello"? На что мы можем ответить: черт возьми, да.
Если бы в этот момент кто-то еще читал, этот читатель счел бы вышеперечисленное абсурдным абсурдным упражнением в очевидном. Тем не менее, этот самый абсурд служит цели, так как кажется абсурдным только в том, что он является бессмысленным повторением, лишенным ценности или понимания первоначального метода. Этот силлогизм, однако, представляет чистую логику; и если он получен незапятнанным из исходного кода, то этот исходный код должен также представлять чистую логику, таким образом идя довольно далеко к ответу на вопрос введения.
getSubject()Теорема.
private String getSubject(int i) {
if (i == 0) {
return "Fred";
}
if (i == 1) {
return "world";
}
return "everybody";
}
Метод getSubject()предлагает чуть более реалистичный пример программирования, чем Mortal Aristotle . Выражает ли это условную предпосылку modus ponens? Есть ли у него предшественник и следствие? Это действительно так.
Антецедентом является предикат, что значение аргумента i, является целым числом, которое является 0или, 1или это ни, 0ни 1. То есть, iимеет состав набора значений { 0, 1, ни ( 0, 1)}, который не обсчитывать компрессы: i∈ { 0, 1ни ( 0или 1)} . Предикат i, это оценивает как истинное или ложное точно так, как должно предшествовать modus ponens. (Чтобы избежать чрезмерной детализации, мы не написали этот третий элемент какiбыть членом набора, исключая другие значения; студент должен принять это, «ни», скорее по номинальной стоимости. На самом деле, компьютерные системы не могут перечислять множество целых чисел, которые охватывают бесконечный диапазон, поэтому здесь происходит множество защемлений и приглушений с извинениями перед логиками повсюду.)
Последовательность выражает, что этот метод оценивает к некоторому значению, x, которое является или "Fred"или "world"или "everybody"; то есть он оценивается как x| x∈ { "Fred", "world", "everybody"} . (Эта вертикальная черта гласит: «Так, что», поэтому неофициальный перевод этого результата будет: «Этот метод оценивается до некоторого значения x, такого, что этот x равен "Fred"или "world"или» "everybody".) Эти шесть терминов, конечно, не случайно нанесены друг на друга; только конкретное значение iкарты для конкретной оценки. Опять же, для того, чтобы этот пост был управляемым, должно быть достаточно сопоставления набор-набор, оставляя сопоставления элемент-элемент в качестве упражнения для ученика.
Таким getSubject()образом, метод занимает свое место в качестве условной предпосылки в силлогизме:
getSubject(i)знак равно
-
i∈ {0,1, ни (0или1)} → принимает значениеx|x∈ {"Fred","world","everybody"} -
i∈ {0,1ни (0или1)} - ∴ оценивает до
x|x∈ {"Fred","world","everybody"}
Раздражает педантизм снова. Теперь мы можем причину об этом методе, устанавливающее истинность вопроса: дается i∈ { 0, 1, ни ( 0или 1)} делает применение этого метода не вычисляться x| x∈ { "Fred", "world", "everybody"}? И снова немного снижается: i∈ { 0, 1ни ( 0или 1)}, getSubject(i)== принимает значение x| x∈ { "Fred", "world", "everybody"}? На что можно смело утверждать: да.
showGreeting()Теорема.
private void showGreeting(String hail, String subject) {
System.out.println(hail + ", " + subject + ".");
}
showGreeting()отличается от getHello()того, что принимает аргументы, но не возвращает значения. Это еще раз представляет небольшую трудность, логики утверждают, что «не возвращает значения» переводится в тривиальный логический случай, когда метод всегда оценивается как: true.
Таким образом, showGreeting()все еще можно рассматривать как условную предпосылку теоремы modus ponens с условным предшественником, состоящим в том, что два аргумента, arg1и arg2, являются Strings. Этот метод, следовательно, имеет сложное утверждение как предшествующее: это arg1a Stringи arg2есть a String. Снова заимствуя из логической символики и используя ∧ в качестве символа для логического И, мы можем написать это составное утверждение как: arg1∈ String∧ arg2∈String .
Но что за System.out.println()утверждение? Это теорема? Как это вписывается в загадку?
Здесь в ходе исследования проводится различие между исследуемым исходным кодом и функциями системы, поддерживающими этот исходный код. Исходный код можно считать «внутренним» и в центре внимания. Функции вспомогательной системы можно считать «внешними» и, несмотря на их очевидную важность, неинтересными. Логики с радостью утверждают, что такая внешняя функциональность находится «вне области дискурса», где границы этого домена — как границы домена всех логических усилий — согласованы, но в конечном итоге произвольны, причем цель заключается в самосогласованности, а не в полноте. По сути, мы будем игнорировать все вызовы функций за пределами исходного кода.
Таким образом, заключение этой теоремы гарантирует постоянную оценку: true и, следовательно, дает следующий силлогистический формат.
showGreeting(arg1, arg2)знак равно
-
arg1∈String∧arg2∈String→ верно -
arg1∈String∧arg2∈String - ∴ правда
greet()Теорема.
void greet() {
String hello = getHello();
String subject = getSubject(1);
showGreeting(hello, subject);
}
greet()объединяет теоремы, которые до сих пор рассматривались, и обнаруживает довольно слабое различие между аксиомой, леммой и теоремой. Мы будем считать метод аксиомой, если он не зависит ни от какой другой внутренней теоремы в отношении ее логической целостности. Таким образом, все изученные до сих пор теоремы являются аксиомами в том смысле, что они могут зависеть от внешних теорем (поддерживающих системные функции вне области дискурса), но внутренне они автономны и ни от чего не зависят. В своей независимости аксиома выражает простоту, достаточную, мы надеемся, сделать ее «изначально принятой» для всех. Метод должен быть леммой, если он зависит от других методов, а другие методы зависят от него, тогда как метод должен быть теоремой, только если другие методы не зависят от него.
greet()затем представляет нашу первую истинную теорему, в отличие от аксиомы, в ее очевидной зависимости от других внутренних аксиом в рассматриваемом исходном коде. Но как мы логически анализируем greet()? Это тоже модус поненс?
Не принимая аргументов и не возвращая значений, greet()кажется, что и условный антецедент, и последующий являются просто истинными , соблазняя довольно скучную интерпретацию:
greet() = правда → правда
Напомним, однако, что Java моделирует утверждение вывода посредством вызова метода. Таким образом, вызов методов внутри greet()подразумевает расширение антецедента для выполнения некоторого дальнейшего тяжелого подъема и включения утверждения всех вызванных им методов.
greet()по существу, вызывает showGreeting()с конкретными аргументами, первый возвращается из getHello(), второй из getSubject(). С логической точки зрения getHello(), getSubject()и showGreeting()это утверждения или предикаты, которые оценивают как истинные или ложные, как мы уже видели в неусвояемых деталях. greet()должны сделать эти утверждения и объединить их, чтобы создать свою собственную истину или ложь, комбинацию, достигнутую путем логического И трех аксиом, чтобы получить их объединенную правду. Это приводит к крайне неудачному разложению логики следующим образом.
greet()= (Правда, getHello()== имеет значение "Hello") ∧ ( 1∈ { 0, 1ни ( 0или 1)}, getSubject(1)== принимает значение x| x∈ { "Fred", "world", "everybody"}) ∧ ( getHello()∈ String, getSubject(1)∈ String, showGreeting(getHello(), getSubject())== TRUE) → верно
Чудовищная силлогистическая форма еще хуже.
greet()знак равно
-
greet()= (Правда,getHello()== имеет значение"Hello") ∧ (1∈ {0,1ни (0или1)},getSubject(1)== принимает значениеx|x∈ {"Fred","world","everybody"}) ∧ (getHello()∈ String,getSubject(1)∈ String,showGreeting(getHello(), getSubject())== TRUE) → верно -
greet()= (Правда,getHello()== имеет значение"Hello") ∧ (1∈ {0,1ни (0или1)},getSubject(1)== принимает значениеx|x∈ {"Fred","world","everybody"}) ∧ (getHello()∈ String,getSubject(1)∈ String,showGreeting(getHello(), getSubject())== верно) - ∴ правда
Естественно, ни один здравомыслящий программист не рассматривает подобные программы. Кроме того, несмотря на Хоара и Дейкстру, немногие рекомендуют это делать. Это, опять же, вряд ли имеет значение: программы можно смотреть так. Их можно рассматривать так, потому что существует эквивалентность между традиционным теоретическим и программным представлениями лежащей в основе логики. Эта эквивалентность образует подушку, на которой комфортно утверждается, что программы, обе из которых используют одну и ту же логику, являются теоремами. Не только это, но и программы воплощают некоторые из самых мощных и фантастически запутанных теорем, когда-либо задуманных человеком, с несравненными логиками истории программистов.
Теоремы в цифровом мире.
Чтобы перетащить нас обратно в реальность для разработчиков, давайте погрузимся в исходный код случайно выбранного продукта с открытым исходным кодом. В июле 2013 года Apache выпустил последнюю версию Lucene , своей популярной системы текстового поиска. На рисунке 1 представлена диаграмма спойклина основного кувшина Lucene, в котором кружок представляет метод.

Рисунок 1: Люцен
Вышеуказанный хаос Поллока в результате разбрызгивания всех 9214 методов на один холст и обводки тонкой серой линией представляет каждую из 127 000 переходных зависимостей. Эти зависимости, стекающие вниз по странице, на диаграмме показаны все методы, которые являются теоремами вверху и размазаны в довольно неинформативную горизонтальную полосу. Методы нижнего черного цвета указывают на аксиомы, зависящие от других, а белые и красные методы указывают на леммы, как зависимые, так и зависимые.
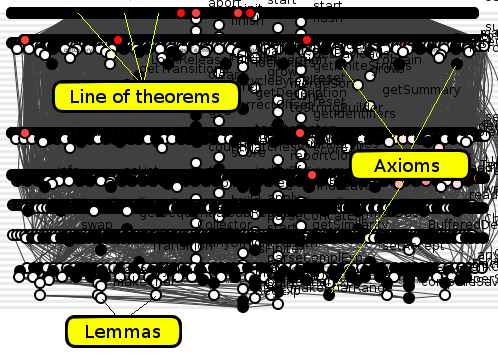
Рисунок 2: Lucene с выделенными компонентами
Так сколько же теорем составляют это реальное, критически важное для бизнеса программное обеспечение? 4289. Lucene делает 4289 заявлений о реальности, и, делая эти заявления, мир приобретает новую систему текстового поиска.
Давайте подробнее рассмотрим любой метод Lucene, скажем getTerms()ниже.
/** This method may return null if the field does not exist.*/
public static Terms getTerms(IndexReader r, String field)
throws IOException {
final Fields fields = getFields(r);
if (fields == null) {
return null;
} else {
return fields.terms(field);
}
}
С нашими очертаниями теорем мы видим, что этот метод явно вытекает из других теорем и аксиом в исходном коде Lucene. Рисунок 3 отражает этот вывод с заполненными кружками, представляющими внутренние аксиомы.
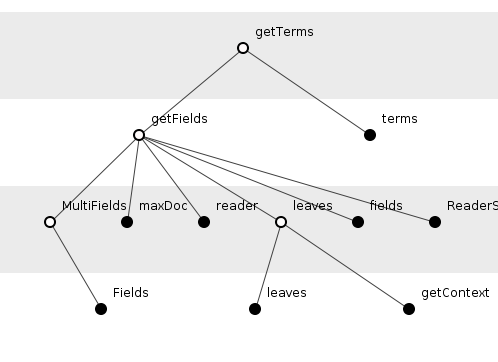
Рисунок 3: получение getTerms ()
getTerms()вытекает из восьми аксиом, трех лемм. Является ли getTerms()сама теорема или лемма? Оказывается, это лемма. Полученные из нее теоремы показаны на рисунке 4, на этот раз теоремы выделены закрашенными кружками.
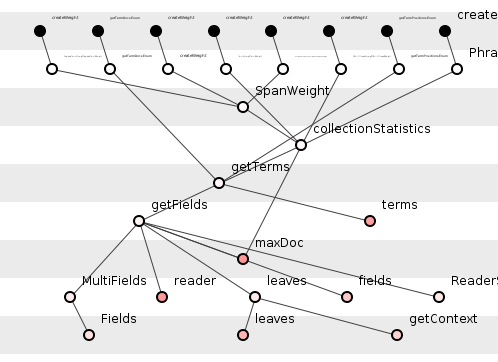
Рисунок 4: getTerms () в полном контексте
Восемь теорем проистекают из getTerms(), утверждая свои истины.
Итак, является ли программа набором теорем?
Мы снова говорим: черт, да.
Резюме.
Доктор Кто Повелитель Времени.
Он путешествует в пространстве и времени в синей коробке под названием ТАРДИС .
Би-би-си послала документальную съемочную группу с Доктором во время его визита, в далеком 1981 году, на планету Логополис , где они сообщили о цивилизации, которая создала материю из чистой математики на том основании, что, как было объявлено перед камерой, «Структура сущность материи и сущность структуры — математика «.
Точно так же структура современных программ показывает, что они являются гигантскими собаками логики, инкрустированными горгульями: тысячи и тысячи теорем делают смелые утверждения, основанные на тысячах и тысячах лемм и аксиом, порождая — волшебным образом и из одного лишь выражения логики — цифровые продукты, без которых современность была бы немыслима.
Разве это не удивительно?
Фото кредитная атрибуция.
CC image Tardis_Trans предоставлено « Смелым библиотекарем на Flickr».
CC изображение Vwooorp любезно предоставлено субкультурой на Flickr.
Изображение CC DSC_0119_2 любезно предоставлено болотным драконом на Flickr.


