Возможно, вы слышали о Graal, новом JIT-компиляторе для JVM, написанном на Java. Он доступен внутри JDK, начиная с Java10, и в будущем, вероятно, станет стандартом JDK.
Если вы заинтересованы, вы можете найти более подробную информацию здесь: https://www.infoq.com/articles/Graal-Java-JIT-Compiler
В прошлом году я в основном работал с Kotlin, и в качестве личного проекта я реализовал бота для игры в Go в Kotlin. Вы можете найти источник здесь: https://github.com/uberto/kakomu
Как вы можете себе представить, в любом Game Bot (Chess, Go и т. Д.) Возможности компьютерного игрока прямо пропорциональны его скорости. В моем случае основной движок основан на алгоритме MonteCarloSearch, который моделирует тысячи случайных игр для оценки каждой позиции.
Так почему бы не дать ему поработать с Граалем?
Начиная с Java 10, вы можете активировать Graal, просто используя VMOptions при запуске.
Сначала несколько слов о методологии тестирования:
|
1
2
3
4
5
6
7
8
9
|
All tests run on my Notebook with i7 2.0Ghz 16Gb Ubuntu 18.4 with OpenJdk 11graal VM Options: -Xms6g -Xmx6g -XX:+UseParallelOldGC -XX:+UnlockExperimentalVMOptions -XX:+UseJVMCICompilerc2 VM Options: -Xms6g -Xmx6g -XX:+UseParallelOldGCI run a test called PerformanceTest in each project which execute a end to end benchmark continuously. In this way the compiler cannot optimize the code for a specific case. Then I choose the faster result, assuming it is the one without GC and OS pauses. All tests are running mono-thread. |
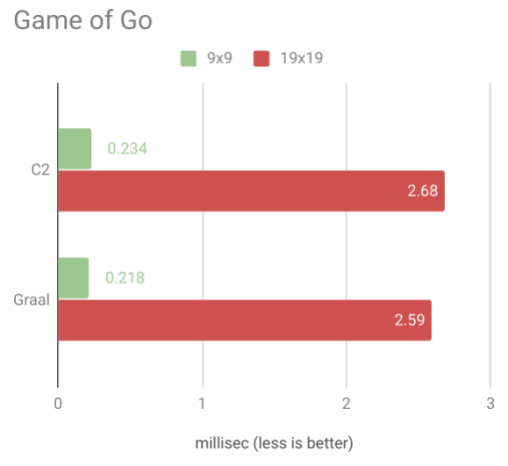
И вот результаты:
Как видите, скомпилированный Graal Kotlin заметно быстрее на малой доске и лишь незначительно быстрее при случайных играх на большой доске.
Я подозреваю, что это связано с тем, что при увеличении памяти системная плата занимает большую часть времени работы. В любом случае прирост более чем приветствуется, особенно если учесть, что я обычно играю на меньшей доске.
Чтобы проверить свою теорию, я создал новый проект с реализацией классических алгоритмов, чтобы увидеть разницу в производительности. Вы можете найти его здесь: https://github.com/uberto/kotlin-perf
На данный момент существует два таких алгоритма: генератор множеств Мандельброта и решатель ранцев.
Мандельброт
Ссылка на Википедию: https://en.wikipedia.org/wiki/Mandelbrot_set
Набор Мандельброта, вероятно, самая известная фрактальная форма, и вы, возможно, видели ее, даже если не знаете названия.
Математически определяется как набор всех точек в комплексной плоскости, где функция z <- z ^ 2 + c не будет расходиться при повторении. Довольно просто сгенерировать множество, повторяющее функции для некоторых точек на комплексной плоскости и создающее из них изображение.
Поскольку целью здесь является производительность, а не графика, я упростил задачу с помощью текстовой графики.
Давайте начнем смотреть на код для набора Мандельброта.
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
|
data class Complex(val r: Double, val i: Double){ operator fun times(other: Complex) = Complex( r = this.r * other.r - this.i * other.i, i = this.i * other.r + this.r * other.i ) operator fun plus(other: Complex) = Complex(r = this.r + other.r, i = this.i + other.i) operator fun minus(other: Complex) = Complex(r = this.r - other.r, i = this.i - other.i) fun squared() = this * this fun squaredModule() = r * r + i * i fun Double.toComplex() = Complex(r=this, i=0.0)} |
|
1
2
3
4
5
6
7
8
9
|
fun mandelSet(initZ: Complex, c:Complex, maxIter: Int): Int { var z = initZ (1..maxIter).forEach{ z = z.squared() + c if (z.squaredModule() >= 4) return it } return maxIter} |
Здесь вы можете увидеть, как использование перегрузки операторов и класса данных для представления комплексных чисел может действительно упростить код и облегчить понимание.
После того, как мы определили в классе Complex правила для выполнения операций над комплексными числами, функция mandelSet должна только проверить, «экранирует» ли операция z <- z ^ 2 + c, и в случае, если после скольких итераций она превысит порог 4.
Здесь вы можете увидеть характерную кардиоидную форму множества Мандельброта в выводе, представленном в AsciiArt:
Проблема с рюкзаком
Справочник по проблеме рюкзака в Википедии: https://en.wikipedia.org/wiki/Knapsack_problem
Задача о ранце может быть определена несколькими способами. Представьте, что вы вор, который ворвался в магазин часов. Вы можете украсть столько часов, сколько захотите, при условии, что вы не превышаете максимальный вес, который вы можете нести на своем рюкзаке.
Будучи рациональным вором, вы определенно хотите оптимизировать ценность часов, которые вы будете приносить с собой. Каждые часы имеют цену и вес. Таким образом, вам нужно найти набор часов с максимальной общей стоимостью для данного веса.
Реальные приложения включают оптимизацию разрезов и материалов для приложений с ЧПУ и маркетинговые стратегии для распределения рекламного бюджета.
Например, давайте начнем с магазина только с 3 часами, определенными так:
|
1
2
3
4
5
|
val shop = Knapsack.shop( Watch(weight = 1, price = 1), Watch(weight = 3, price = 2), Watch(weight = 1, price = 3)) |
Если у нас максимальный вес 1, нам лучше взять третьи часы, а не первые, потому что значение выше.
Если у нас максимальный вес 3, мы можем выбрать число 2 (цена 2) или число 1 и 3 (цена 1 + 3). В этом случае лучше подобрать 1 и 3, даже если их общий вес меньше максимального.
Это комплексные решения для этого магазина:
|
1
2
3
4
5
|
assertEquals(3, selectWatches(shop, maxWeight = 1))assertEquals(4, selectWatches(shop, maxWeight = 2))assertEquals(4, selectWatches(shop, maxWeight = 3))assertEquals(5, selectWatches(shop, maxWeight = 4))assertEquals(6, selectWatches(shop, maxWeight = 5)) |
Как вы видите, с увеличением количества доступных часов количество возможных вариантов выбора очень и очень быстро возрастает. Это классическая проблема NP-Hard.
Чтобы решить это в разумные сроки, нам нужно немного обмануть и использовать динамическое программирование. Мы можем построить карту с уже оптимизированным решением для каждого набора часов, чтобы избежать их пересчета каждый раз.
Общий алгоритм основан на исчерпывающем поиске на основе рекурсии. Это код Котлина для его решения, разделенный функцией запоминания и рекурсивным поиском максимального значения.
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
typealias Memoizer = MutableMap<String, Int>fun priceAddingElement(memo: Memoizer, shop: Set<Watch>, choice: Set<Watch>, maxWeight: Int, priceSum: Int): Int = shop.filter { !(it in choice) && it.weight <= maxWeight } .map { selectWatches( memo, shop, maxWeight - it.weight, choice + it, priceSum + it.price) } .filter { it > priceSum } .max() ?: priceSumfun selectWatches(memo: Memoizer, shop: Set<Watch>, maxWeight: Int, choice: Set<Watch>, priceSum: Int): Int = memoization(memo, generateKey(choice)) { priceAddingElement(memo, shop, choice, maxWeight, priceSum)}private fun memoization(memo: Memoizer, key: String, f: () -> Int): Int = when (val w = memo[key]) { null -> f().also { memo[key] = it } else -> w } |
Мне очень нравится, как Котлин позволяет четко выразить намерение, не повторяя себя. Если вы не знаете Kotlin, я надеюсь, что этот код заинтригует вас настолько, что когда-нибудь попробует.
Ориентиры
А теперь та часть, которую вы все время ждали. Давайте сравним производительность Graal и старого доброго компилятора C2.
Давайте вспомним, что Graal написан на Java и использует преимущества новых исследований в области компиляции, но он все еще относительно молод. С2 с другой стороны очень хорошо настроен и зрел.
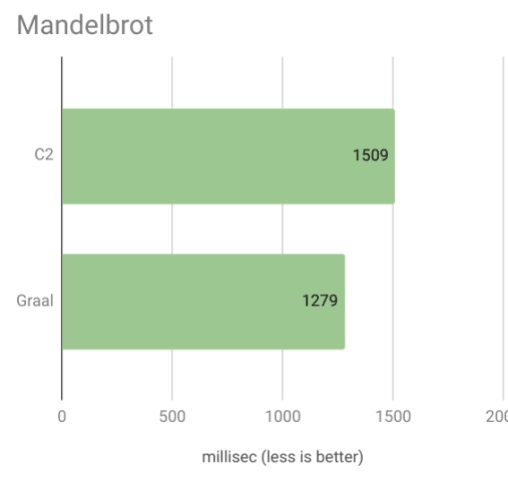
Первый сюрприз с примером Мандельброта:
Честно говоря, я не ожидал такой большой разницы в производительности. Грааль примерно на 18% быстрее, чем С2! Просто чтобы быть уверенным, что я попробовал с немного другими формулами с теми же результатами. Грааль действительно сияет при компиляции расчетов, выполненных в Котлине.
А теперь для еще большего сюрприза, тест на рюкзак: 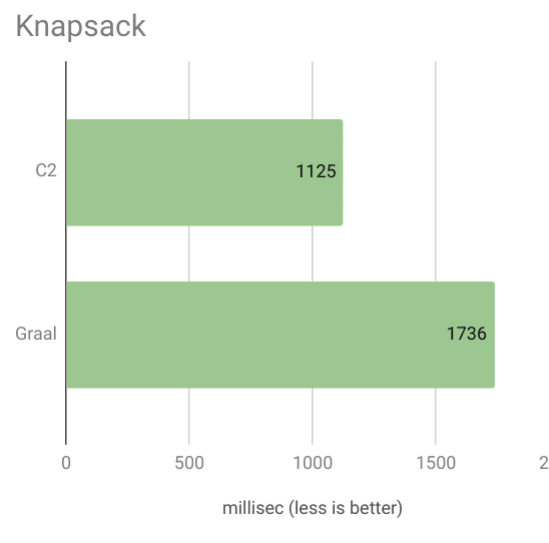
Здесь Грааль на 54% медленнее!
Выполнив некоторое профилирование, я обнаружил, что мой код большую часть времени тратит на функцию, которая генерирует ключ для запоминания.
Чтобы быть верным, я заказал набор и затем преобразовал в строку. Это много ненужной работы и зависит от реализации HashSet Java.
Поэтому я изменил метод для генерации ключа из этого:
|
1
|
private fun generateKey(choice: Set<Watch>): String = choice.sortedBy { "${it.price}-${it.weight}" }.toString() |
К этому:
|
1
2
|
private fun generateKey(choice: Set<Watch>): String = choice.map{ it.hashCode() }.sorted().joinToString("") |
Новая функция работает быстрее, потому что она сортирует хэши Watches (которые являются уникальными), а затем просто объединяет их в строку.
Обратите внимание, что мы не можем просто использовать хэш набора, потому что может быть конфликт хэшей. Я действительно попробовал это и подтвердил, что это начало давать неправильные результаты.
Можно создать более безопасный метод хеширования для Set, но цель здесь не в том, чтобы максимально оптимизировать алгоритм, а в том, чтобы написать эффективный и понятный код Котлина.
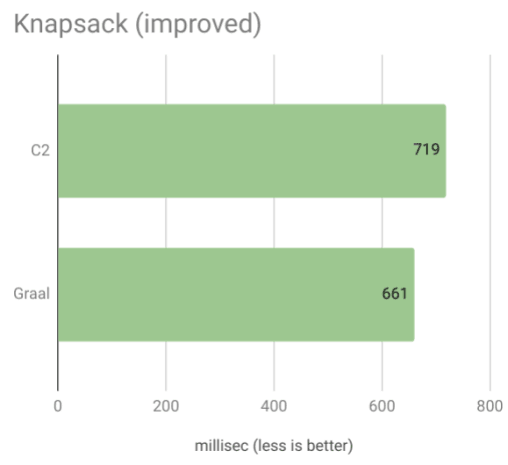
А теперь результаты для идиоматического Котлина:
Здесь Graal снова заметно быстрее, чем C2, и в целом новый генератор ключей намного быстрее, чем в предыдущей реализации.
Я полагаю, что эти результаты сильно оптимизированы (с использованием встроенных функций и т. Д.) Для типичного использования Java, в то время как Graal превосходен при компиляции небольших методов и легких объектов, которые типичны для идиоматического Kotlin.
Все это заслуживает дальнейшего изучения, но я надеюсь, что этот пост может побудить больше разработчиков Kotlin использовать Graal.
Если вас интересуют другие похожие посты, пожалуйста, следите за моей учетной записью в Twitter @ramtop или посмотрите мой блог.
| Опубликовано на Java Code Geeks с разрешения Уберто Бабрини, партнера нашей программы JCG. Смотрите оригинальную статью здесь: Сравнение производительности Kotlin с Graal и C2
Мнения, высказанные участниками Java Code Geeks, являются их собственными. |