Одна из замечательных особенностей класса java.util.Random в Java 8 заключается в том, что он был модернизирован и теперь возвращает случайный поток чисел.
Например, чтобы генерировать бесконечный поток случайных двойных чисел от 0 (включительно) до 1 (исключая):
|
1
2
|
Random random = new Random();DoubleStream doubleStream = random.doubles(); |
или генерировать бесконечный поток целых чисел от 0 (включительно) до 100 (исключая):
|
1
2
|
Random random = new Random();IntStream intStream = random.ints(0, 100); |
Итак, для чего можно использовать этот бесконечный случайный поток, я покажу несколько сценариев, но имейте в виду, что, поскольку это бесконечный поток, любые терминальные операции должны выполняться после того, как поток каким-то образом ограничен, иначе операция не прекратится!
Например, получить поток из 10 случайных целых чисел и вывести их:
|
1
|
intStream.limit(10).forEach(System.out::println); |
Или создать список из 100 случайных чисел:
|
1
2
3
4
|
List<Integer> randomBetween0And99 = intStream .limit(100) .boxed() .collect(Collectors.toList()); |
Для гауссовых псевдослучайных значений не существует потокового эквивалента random.doubles (), однако легко придумать тот, который предоставляет Java 8:
|
1
2
|
Random random = new Random();DoubleStream gaussianStream = Stream.generate(random::nextGaussian).mapToDouble(e -> e); |
Здесь я использую вызов API Stream.generate, передаваемый поставщику, который генерирует следующий гауссиан с уже доступным методом в классе Random .
Так что теперь, чтобы сделать что-то немного более интересное с потоком псевдослучайных двойных чисел и потоком гауссовых псевдослучайных двойных чисел, я хочу получить распределение двойных чисел для каждого из этих двух потоков, ожидая, что Распределение при построении должно быть равномерно распределено для псевдослучайных двойных чисел и должно быть нормальным распределением для гауссовых псевдослучайных двойных чисел.
В следующем коде я создаю такое распределение для миллиона псевдослучайных значений, в нем используется множество средств, предоставляемых новым Java 8 Streams API:
|
1
2
3
4
5
6
7
8
|
Random random = new Random();DoubleStream doubleStream = random.doubles(-1.0, 1.0);LinkedHashMap<Range, Integer> rangeCountMap = doubleStream.limit(1000000) .boxed() .map(Ranges::of) .collect(Ranges::emptyRangeCountMap, (m, e) -> m.put(e, m.get(e) + 1), Ranges::mergeRangeCountMaps);rangeCountMap.forEach((k, v) -> System.out.println(k.from() + "\t" + v)); |
и этот код выплевывает данные по этим направлениям:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
|
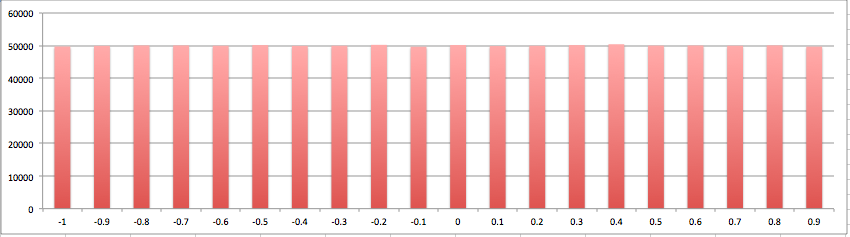
-1 49730-0.9 49931-0.8 50057-0.7 50060-0.6 49963-0.5 50159-0.4 49921-0.3 49962-0.2 50231-0.1 496580 501770.1 498610.2 499470.3 501570.4 504140.5 500060.6 500380.7 499620.8 500710.9 49695 |
и аналогичным образом генерируют распределение для миллиона гауссовских псевдослучайных значений:
|
01
02
03
04
05
06
07
08
09
10
11
|
Random random = new Random();DoubleStream gaussianStream = Stream.generate(random::nextGaussian).mapToDouble(e -> e);LinkedHashMap<Range, Integer> gaussianRangeCountMap = gaussianStream .filter(e -> (e >= -1.0 && e < 1.0)) .limit(1000000) .boxed() .map(Ranges::of) .collect(Ranges::emptyRangeCountMap, (m, e) -> m.put(e, m.get(e) + 1), Ranges::mergeRangeCountMaps);gaussianRangeCountMap.forEach((k, v) -> System.out.println(k.from() + "\t" + v)); |
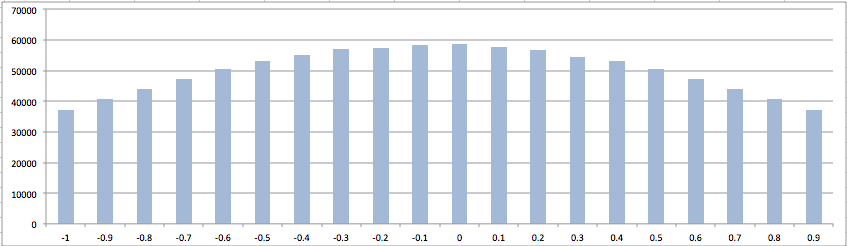
Построение данных дает ожидаемый результат:
Для псевдослучайных данных:
И для гауссовых данных:
- Полный код доступен в гисте здесь — https://gist.github.com/bijukunjummen/8129250