Реализация Word Ladder Game с использованием Neo4j

Word Ladder  — довольно популярная игра, изобретенная  Льюисом Кэрроллом , который более известен как автор книги «Алиса в стране чудес».

В загадке «Лестница слов» вы должны постепенно вносить изменения, меняя одну букву за раз. На каждом этапе вы должны преобразовать одно слово в другое слово, вам не разрешено превращать слово в неслове. Например, слово «FOOL» может быть преобразовано в слово «SAGE» как

FOOL

POOL

ОПРОС

ПОЛЮС

Бледно

ПРОДАЖА

SAGE

Есть много вариантов головоломки слова лестницы. Например, вам может быть дано определенное количество шагов для выполнения преобразования, или вам может потребоваться использовать определенное слово. В этом разделе мы заинтересованы в выяснении наименьшего числа преобразований, необходимых для превращения начального слова в конечное слово.

Однако наилучшее решение проблемы Word Ladder — это использование графиков, а с Neo4j это еще проще.

Вот схема того, куда мы идем:

• Представьте отношения между словами в виде графика.
• Используйте алгоритм графа, известный как поиск в ширину, чтобы найти эффективный путь от начального слова до конечного слова.

Построение словесного графа

Наша первая задача — выяснить, как превратить большую коллекцию слов в граф. Мы хотели бы иметь отношение от одного слова к другому, если два слова отличаются только одной буквой. Если мы сможем создать такой график, то любой путь от одного слова к другому является решением головоломки «лестница слова».

Запись слов на график — это еще одна прекрасная проблема.

Мы могли бы использовать несколько разных подходов для создания графа, который нам нужен для решения этой проблемы. Начнем с предположения, что у нас есть список слов одинаковой длины. В качестве отправной точки мы можем создать вершину в графе для каждого слова в списке. Чтобы выяснить, как соединить слова, мы могли бы сравнить каждое слово в списке друг с другом. Когда мы сравниваем, мы смотрим, сколько букв разные. Если два рассматриваемых слова отличаются только одной буквой, мы можем создать ребро между ними на графике. Для небольшого набора слов этот подход будет хорошо работать; однако давайте предположим, что у нас есть список из 5110 слов. Грубо говоря, сравнение одного слова с каждым другим словом в списке является алгоритмом O (n2). Для 5110 слов n2 — это более 26 миллионов сравнений.

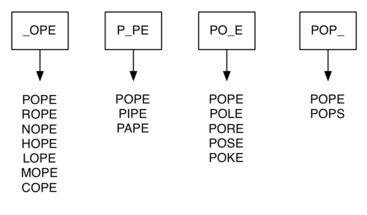
Мы можем сделать намного лучше, используя следующий подход. Предположим, что у нас есть огромное количество сегментов, каждое из которых имеет четырехбуквенное слово снаружи, за исключением того, что одна из букв в метке была заменена подчеркиванием. Например, рассмотрим изображение ниже, у нас может быть поле с надписью «pop_». Когда мы обрабатываем каждое слово в нашем списке, мы сравниваем слово с каждым сегментом, используя ‘_’ в качестве подстановочного знака, поэтому и «pope», и «pops» будут соответствовать «pop_». Каждый раз, когда мы находим соответствующее ведро, мы помещаем наше слово в это ведро. Как только у нас есть все слова в соответствующих корзинах, мы знаем, что все слова в корзине должны быть связаны.

В Java это может быть реализовано с использованием карты в качестве очевидного решения .. см. Фрагмент ниже

public class WordGraph {

Map<String, Node> nodeMap;
GraphDatabaseService graphDb;

public WordGraph(){
  graphDb = NeoDatabaseHandler.getGraphDatabase();
  nodeMap = new HashMap<String, Node>();
}

private Node getNode(String word){
  if(!nodeMap.containsKey(word)){
   Node node = graphDb.createNode(NeoHelper.WordLabel.WORD);
   node.setProperty("word", word);
   nodeMap.put(word, node);
  }
  return nodeMap.get(word);
}

public void addEdge(String parentWord, String childWord){
  Node parentNode = getNode(parentWord);
  Node childNode = getNode(childWord);
  parentNode.createRelationshipTo(childNode, NeoHelper.RelationshipTypes.MOVE);
}
}

Всякий раз, когда нам нужно создать ребро, мы просто вызываем метод addEdge, и он позаботится обо всем остальном.

Итак, мы перебираем сегменты и записываем слова и их отношения в график для (List <String> mappedWordsParent: wordMap.values ​​()) {

  for (String parentWord : mappedWordsParent) {
    for (String childWord : mappedWordsParent) {
      if(!childWord.equals(parentWord)){
        wordGraph.addEdge(parentWord, childWord);
      }
    }
  }
}

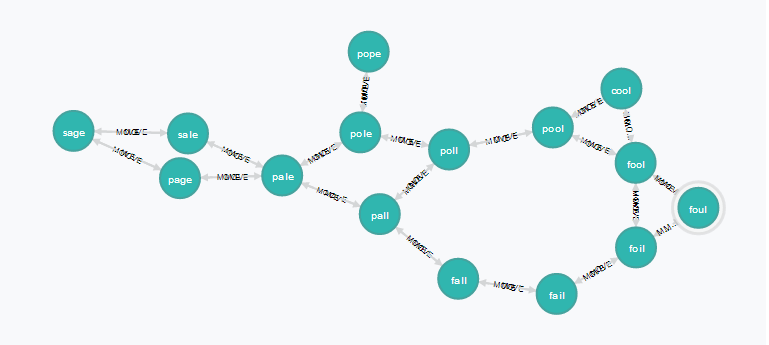
График, созданный с использованием минимального набора слов, будет выглядеть так, как показано ниже (извинения за беспорядок в именах отношений)

Как только у нас есть готовый график, мы можем сделать приличный обход, чтобы получить требуемый путь. Допустим, мы пытаемся найти путь от  дурака  к  мудрецу

Алгоритм графа, который мы собираемся использовать, называется алгоритмом поиска в ширину. Поиск в ширину  ( BFS ) — это один из самых простых алгоритмов поиска в графе.

graphDb
.traversalDescription().breadthFirst()
                       .relationships(NeoHelper.RelationshipTypes.MOVE)
                       .evaluator(Evaluators.includeWhereEndNodeIs(endNode))
                       .traverse(startNode)