Статьи

Подход на основе DSL для ввода данных графов в Java-программах на основе теории графов

Февраль 25, 2019

Большинство из нас написали несколько программ, которые имеют дело с алгоритмами теории графов, такими как нахождение кратчайшего пути между двумя вершинами, нахождение минимального остовного дерева для данного графа и так далее. В каждом из этих алгоритмов программный способ представления графа состоит в том, чтобы использовать либо матрицу смежности, либо список смежности . Оба они не очень интуитивно понятный способ определения ввода графика. Например, матрица смежности может привести к ошибкам, если записи не сделаны в правильных столбцах и строках. Более того, во время выполнения вы не очень уверены, какая строка / столбец представляет какое ребро, и все становится еще сложнее, когда дело доходит до ввода для графа с большим количеством вершин.

Во время инженерных исследований я реализовал довольно много графовых алгоритмов на Java, и во всех них у меня были вложенные циклы for для получения входных данных матрицы смежности. Недавно, когда я читал книгу DSL Мартина Фаулера, я натолкнулся на идею создания DSL для обеспечения ввода графа, то есть DSL, который позволил бы пользователю указывать вершины, ребра и их веса. Я выбрал графические алгоритмы, которые я реализовал, и просто удалил вход матрицы смежности и вместо этого использовал созданный мной DSL. Алгоритм работал как шарм.

В этой статье я покажу действительный синтаксис для DSL, взяв различные графические входы и показывая для них DSL. Затем я покажу вам созданную мной библиотеку, которая состоит из семантической модели графика, синтаксического анализатора и лексера DSL и простого API-интерфейса разработчика, который заполняет семантическую модель из сценария DSL. Парсер и лексер были сгенерированы с использованием ANTLR, и, следовательно, эта библиотека требует, чтобы ANTLR Jar был доступен в classpath. И, наконец, я покажу, как можно использовать этот DSL для нахождения минимального остовного дерева с помощью алгоритма Крускала.

Синтаксис DSL и некоторые примеры

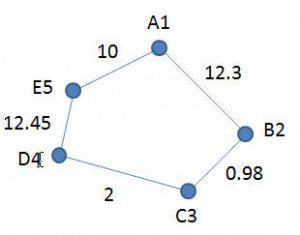
DSL для приведенного ниже графика (g1):

График G1

График G1

1
2
3
4
5
6
Graph {
  A1 -> B2 (12.3)
  B2 -> C3(0.98)
  C3->D4 (2)
  D4 ->E5 (12.45)
}

Обратите внимание, что между элементами в DSL выше есть разные пробелы. Это просто для того, чтобы показать различные способы написания DSL.

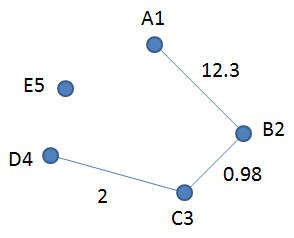
DSL для приведенного ниже графика (g2) будет:

График G2

График G2

1
2
3
4
5
6
Graph{
  A1 -> B2 (12.3)
  B2 -> C3 (0.98)
  C3 -> D4 (2)
  E5
}

Обратите внимание, что между ‘Graph’ и ‘{‘ нет пробела. Это просто для того, чтобы показать разные способы написания.

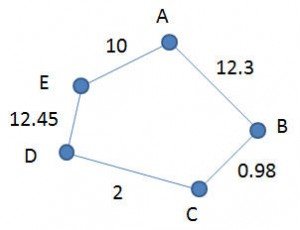
DSL для приведенного ниже графика (g3) будет:

График G3

График G3

1
2
3
4
5
6
Graph {
  A -> B (12.3)
  B -> C (0.98)
  C -> D (2)
  D -> E (12.45)
}

Теперь, чтобы показать некоторые из недопустимых сценариев DSL:

1
2
3
4
Graph {
  1A -> B (12.3)
  B -> C (0.98)
}

Выше недопустимо, потому что имя вершины начинается с цифры.

1
2
Graph {
}

Вышеуказанное недопустимо, потому что Граф ожидает, что будет определена хотя бы одна вершина. Но он может иметь ноль или более ребер.

Библиотека для ввода графиков на основе DSL

Я использовал ANTLR, который выполняет всю задачу по созданию лексера и парсера для грамматики, которую я определил для моего DSL. Таким образом, мне не нужно беспокоиться о создании парсера или беспокоиться о создании токенов из входного скрипта DSL.

Классы parser и lexer вместе с классами семантической модели упакованы в jar, и этот jar вместе с ANTLR jar необходимо включить, чтобы использовать запись DSL для ввода в граф.

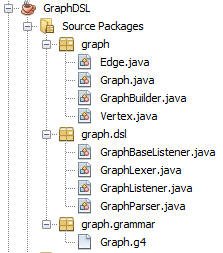
Структуру банки DSL можно увидеть на скриншоте ниже:

GraphDSL Jar

GraphDSL Jar

Классы в пакете графа соответствуют семантической модели, то есть это универсальные классы и могут использоваться независимо от того, использует ли кто-то DSL или нет. Классы в graph.dsl соответствуют сгенерированным ANTLR java-классам для лексера и анализатора.

Грамматика, используемая ANTLR для лексического анализа и анализа:

01
02
03
04
05
06
07
08
09
10
11
12
13
14
grammar Graph;
 
graph: GRAPH_START (edge|vertex)+ GRAPH_END;
edge: (vertex) TO (vertex) weight;
vertex: ID;
weight: '(' NUM ')';
GRAPH_START : 'Graph'([ ])*'{';
GRAPH_END : '}';
WEIGHT_START: '(';
WEIGHT_END: ')';
TO: '->';
ID: ^[a-zA-Z][a-zA-Z0-9]*;
NUM: [0-9]*[.]?[0-9]+;
WS: [ \t\r\n]+ -> skip;

Приведенная выше грамматика имеет возможности для улучшения, но в качестве первой попытки я постаралась удержать ее на этом уровне.

  • Загрузите банку DSL отсюда (GraphDSL.jar).
  • Загрузите банку ANTLR здесь (antlr-4.1-complete.jar).

Примечание. Этот DSL разработан с использованием ANTLR версии 4.

Рекомендуемая книга для внешних DSL, использующих ANTLR: « Шаблоны реализации языка: создайте свой собственный доменспецифический и общий языки программирования»

Алгоритм Крускала для нахождения минимального остовного дерева

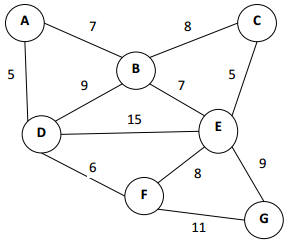
График, который используется для проверки реализации этого алгоритма:

Образец графика

Образец графика

и DSL для того же:

01
02
03
04
05
06
07
08
09
10
11
12
13
Graph  {
  A -> B (7)
  B -> C (8)
  A -> D (5)
  B -> D (9)
  D -> E (15)
  D -> F (6)
  E -> F (8)
  E -> C (5)
  B -> E (7)
  E -> G (9)
  F -> G (11)
}

Давайте посмотрим на реализацию:

001
002
003
004
005
006
007
008
009
010
011
012
013
014
015
016
017
018
019
020
021
022
023
024
025
026
027
028
029
030
031
032
033
034
035
036
037
038
039
040
041
042
043
044
045
046
047
048
049
050
051
052
053
054
055
056
057
058
059
060
061
062
063
064
065
066
067
068
069
070
071
072
073
074
075
076
077
078
079
080
081
082
083
084
085
086
087
088
089
090
091
092
093
094
095
096
097
098
099
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
package kruskalsalgo;
 
import java.util.ArrayList;
import java.util.Collections;
import java.util.Scanner;
import graph.Edge;
import graph.Graph;
import graph.Vertex;
import graph.GraphBuilder;
import java.io.IOException;
import java.util.Comparator;
 
public class KruskalsAlgorithm {
 
  public static void main(String[] args) throws IOException {
 
    //Load the graph data from the DSL
    Graph g = new GraphBuilder().buildGraph("graph.gr");
    ArrayList<Set> forest = new ArrayList<Set>();
    ArrayList<Edge> finalEdgeSet = new ArrayList<Edge>();
 
    //Creating disjoint set of vertices which represents the initial forest
    for (Vertex v : g.getVertices()) {
      Set newSet = new Set();
      newSet.getVertexList().add(v);
      forest.add(newSet); //Creating Disjoint Sets
 
    }
 
    //sort the edges in the graph based on their weight
    Collections.sort(g.getEdges(), new Comparator<Edge>(){
 
      public int compare(Edge o1, Edge o2) {
        return o1.getWeight().compareTo(o2.getWeight());
      }
 
    });
 
    for (Edge edge : g.getEdges()) {
      //Find in which set the vertices in the edges belong
      int rep1 = Set.findRep(edge.getFromVertex(), forest);
      int rep2 = Set.findRep(edge.getToVertex(), forest);
 
      //If in different sets then merge them into one set and pick the edge.
      if (rep1 != rep2) {
        finalEdgeSet.add(edge);
        Set.Union(rep1, rep2, forest);
      }
    }
 
    System.out.println("The Minimum Spanning tree is");
    for (Edge edge : finalEdgeSet) {
      System.out.println("Vertex: " + edge.getFromVertex().getLabel() +
              " to Vertex: " + edge.getToVertex().getLabel());
    }
 
    System.out.println("");
 
  }//End of Main
}
 
class Set {
 
  private ArrayList<Vertex> vertexList;
  private int representative;
  static int count;
 
  public Set() {
    vertexList = new ArrayList<Vertex>();
    this.representative = ++(Set.count);
  }
 
  //Find the set identifier in which the given vertex belongs to.
  public static int findRep(Vertex vertex, ArrayList<Set> forest) {
    int rep = 0;
    for (Set set : forest) {
      for (Vertex v : set.getVertexList()) {
        if (v.getLabel().equals(vertex.getLabel())) {
          return set.getRepresentative();
        }
      }
    }
 
    return rep;
  }
 
  //Find the set given the step identifier.
  public static Set findSet(int rep, ArrayList<Set> forest) {
    Set resultSet = null;
    for (Set set : forest) {
      if (set.getRepresentative() == rep) {
        return set;
      }
    }
    return resultSet;
  }
 
  //Merge the set into another and remove it from the main set.
  public static void Union(int rep1, int rep2, ArrayList<Set> forest) {
    Set set1 = Set.findSet(rep1, forest);
    Set set2 = Set.findSet(rep2, forest);
 
    for (Vertex v : set2.getVertexList()) {
      set1.getVertexList().add(v);
    }
    forest.remove(set2);
  }
 
  public ArrayList<Vertex> getVertexList() {
    return vertexList;
  }
 
  public int getRepresentative() {
    return representative;
  }
}

Приведенный выше код загружает данные графика из dsl-graph.gr. Сценарии DSL должны быть помещены в пакет ресурсов, чтобы библиотека DSL могла найти его.

Выход для вышеуказанного кода:

1
2
3
4
5
6
7
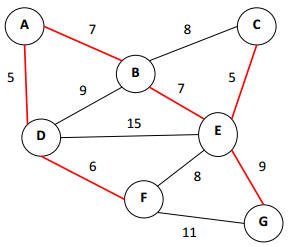
The Minimum Spanning tree is
Vertex: A to Vertex: D
Vertex: E to Vertex: C
Vertex: D to Vertex: F
Vertex: A to Vertex: B
Vertex: B to Vertex: E
Vertex: E to Vertex: G

и показывая то же самое схематично

Минимальное остовное дерево

Минимальное остовное дерево

60
Share: