Мы все были там. Глядя на плохо разработанный код, слушая объяснения автора о том, что никогда не следует жертвовать производительностью ради дизайна. И вы просто не можете убедить автора избавиться от его 500-строчных методов, потому что цепочка вызовов методов может снизить производительность.
Ну, это могло быть правдой в 1996 году или около того. Но с тех пор JVM превратилась в удивительное программное обеспечение. Один из способов узнать об этом — начать углубляться в оптимизацию, проводимую виртуальной машиной. Арсенал методов, применяемых JVM , довольно обширный, но давайте рассмотрим один из них более подробно. А именно метод встраивания . Это проще всего объяснить с помощью следующего примера:
|
1
2
3
4
5
6
7
|
int sum(int a, int b, int c, int d) { return sum(sum(a, b),sum(c, d));} int sum(int a, int b) { return a + b;} |
Когда этот код будет запущен, JVM выяснит, что он может заменить его более эффективным, так называемым «встроенным» кодом:
|
1
2
3
|
int sum(int a, int b, int c, int d) { return a + b + c + d;} |
Вы должны обратить внимание, что эта оптимизация выполняется виртуальной машиной, а не компилятором. Во-первых, непонятно, почему было принято это решение. В конце концов — если вы посмотрите на пример кода выше — зачем откладывать оптимизацию, когда компиляция может дать более эффективный байт-код? Но, учитывая и другие не столь очевидные случаи, JVM — лучшее место для оптимизации: 
- JVM оснащен данными времени выполнения помимо статического анализа. Во время выполнения JVM может принимать лучшие решения, основываясь на том, какие методы выполняются чаще всего, какие нагрузки являются избыточными, когда безопасно использовать распространение копий и т. Д.
- JVM обладает информацией о базовой архитектуре — количестве ядер, размере кучи и конфигурации и, таким образом, может сделать лучший выбор на основе этой информации.
Но давайте посмотрим на эти предположения на практике. Я создал небольшое тестовое приложение, которое использует несколько разных способов сложить 1024 целых числа.
- Относительно разумный, когда реализация просто перебирает массив, содержащий 1024 целых числа, и суммирует результат вместе. Эта реализация доступна в InlineSummarizer.java .
- Основанный на рекурсии подход «разделяй и властвуй». Я беру исходный массив из 1024 элементов и рекурсивно делю его на две половины — первая глубина рекурсии, таким образом, дает мне два массива по 512 элементов, вторая глубина имеет четыре массива по 256 элементов и так далее. Чтобы суммировать все 1024 элемента, я ввожу 1023 дополнительных вызова метода. Эта реализация прикреплена как RecursiveSummarizer.java .
- Наивный подход «разделяй и властвуй». Он также делит исходный массив из 1024 элементов, но с помощью вызова дополнительных методов экземпляра на разделенных половинах, а именно: я вкладываю вызовы sum512 (), sum256 (), sum128 (),…, sum2 (), пока я не суммирую все элементы , Как и в случае с рекурсией, я ввел 1023 дополнительных вызова методов в исходном коде .
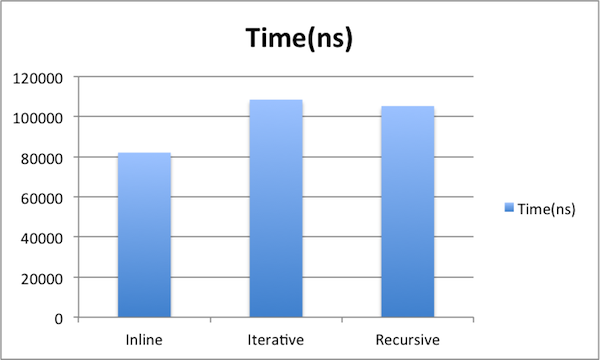
И у меня есть тестовый класс для запуска всех этих образцов. Первые результаты получены из неоптимизированного кода:
Как видно из приведенного выше, встроенный код является самым быстрым. А те, где мы ввели 1023 дополнительных вызова методов, медленнее на ~ 25 000 нс. Но это изображение нужно интерпретировать с оговоркой — это снимок с запусков, где JIT еще не полностью оптимизировал код. В моем MB Pro в середине 2010 года потребовалось от 200 до 3000 запусков в зависимости от реализации.
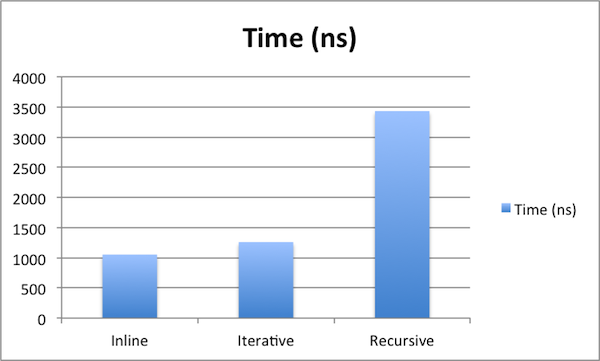
Более реалистичные результаты ниже. Я запускал все реализации сумматора более 1 000 000 раз и отбрасывал прогоны, в которых JIT еще не удалось исполнить свою магию.
Мы видим, что, хотя встроенный код по-прежнему работает лучше, итеративный подход также развивался с приличной скоростью. Но рекурсия заметно отличается — когда итеративный подход приближается всего с 20% накладных расходов, RecursiveSummarizer занимает 340% времени, которое требуется для выполнения встроенного кода. Очевидно, это то, о чем нужно знать — когда вы используете рекурсию, JVM беспомощна и не может выполнять встроенные вызовы методов. Так что помните об этом ограничении при использовании рекурсии.
За исключением рекурсии — накладные расходы метода почти не существуют. Разница всего в 205 нс между 1023 дополнительными вызовами методов в исходном коде. Помните, это были наносекунды (10 ^ -9 с), которые мы использовали для измерения. Таким образом, благодаря JIT мы можем безопасно игнорировать большую часть накладных расходов, вызванных вызовами методов. В следующий раз, когда ваш коллега скрывает свои паршивые дизайнерские решения за утверждением, что копаться в стеке вызовов неэффективно, пусть сначала пройдут небольшой курс JIT . И если вы хотите хорошо подготовиться к тому, чтобы блокировать его будущие абсурдные высказывания, подпишитесь на нашу ленту RSS или Twitter, и мы будем рады предоставить вам будущие тематические исследования.
Полное раскрытие: вдохновение для тестового примера, использованного в этой статье, было инициировано сообщением в блоге Томаша Нуркевича.
Справка: насколько дорогой вызов метода в Java от нашего партнера по JCG Никиты Сальникова Тарновски из блога Plumbr Blog .