В третьей части этой серии кинетической прокрутки JavaScript демонстрируется так называемая функция привязки к сетке . Реализация довольно проста: нужно выяснить, где прокрутка должна остановиться, а затем отрегулировать это целевое положение в соответствии с предполагаемым местоположением.
Во второй части серии обсуждалась техника замедления прокрутки с использованием концепции экспоненциального затухания . В случае пролистывающего списка это означает, что список будет замедляться и останавливаться в какой-то момент, в зависимости от скорости запуска в тот момент, когда пользователь отпускает захват. Оказывается, это также становится важным ключом для реализации привязки к сетке.
Обратите внимание, что кривая экспоненциального затухания позволяет нам знать о двух вещах (1), когда прокрутка остановится (2), где она остановится. Как только скорость запуска известна, эти два значения могут быть вычислены аналитически . Это очень мощно, в частности, поскольку конечная позиция остановки может быть скорректирована сразу. Для быстрой демонстрации перейдите по ссылке ariya.github.io/kinetic/3 (желательно с помощью браузера на смартфоне), пролистайте список и посмотрите, как он всегда останавливается, чтобы выровнять запись цвета по наложенному слоту.
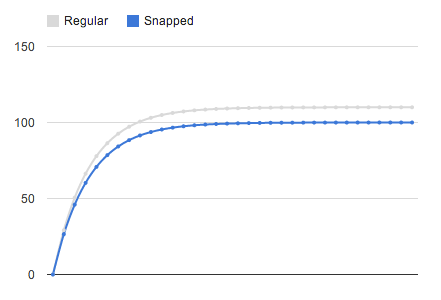
Следующая диаграмма иллюстрирует концепцию. Без привязки к сетке кривая положения прокрутки как функция времени отображается серой линией. Предположим, что окончательная позиция будет на уровне 110 пикселей. Если мы знаем, что сетка привязки — каждые 25 пикселей, то это окончательное положение должно быть откорректировано до 100 пикселей или 125 пикселей. Поскольку первое является ближайшим, это будет конечная конечная позиция, и замедление будет следовать кривой, окрашенной синим цветом.
Соответствующий код для этой функции можно увидеть в репозитории github.com/ariya/kinetic . На самом деле, он не сильно отличается от кода, показанного уже в предыдущей второй части . Новым дополнением является следующий фрагмент:
target = Math.round(target / snap) * snap; |
Здесь переменная snapхранит высоту строки каждого элемента (она вычисляется один раз во время инициализации). Если вы уже ознакомились с реализацией экспоненциального затухания, в ней targetуказана конечная позиция прокрутки после завершения замедления. Без функции привязки мы не изменяем это значение. Когда мы хотим отрегулировать конечную позицию прокрутки, чтобы она была магнитно привязана к ближайшему месту привязки, мы просто меняем это значение.
Также обратите внимание, что нет требования, snapкоторое должно быть константой. Список с неоднородной высотой строки все еще может использовать функцию привязки к сетке. Все, что нам нужно, это массив возможных значений для конечной позиции, и каждая цель замедления должна быть изменена до ближайшего значения. Если вы изучаете физику, это очень похоже на идею дискретных пакетов электромагнитной энергии в квантовой механике .
В некоторых библиотеках, в которых реализована кинетическая прокрутка, привязка к сетке осуществляется путем постоянного отслеживания положения прокрутки. Когда он собирается остановиться, то положение корректируется для перемещения в максимально близкое положение на основе расстояния сетки. Мало того, что это приводит к более сложному коду, такой подход имеет большой недостаток. В некоторых случаях список может выйти за рамки, прежде чем он отскочит назад, и, следовательно, он вообще не демонстрирует эффект плавной прокрутки. С аналитической техникой, описанной здесь, этот неловкий эффект не произойдет вообще. Как всегда, правильное решение часто приходит с самой чистой реализацией!
Что будет показано в четвертой части? Давайте держать это как сюрприз!
