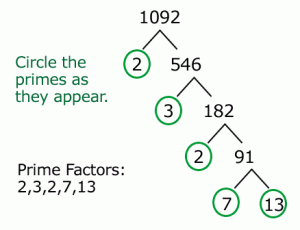
Одна из распространенных домашних заданий / заданий на курсах по программированию — это Prime Factorization. Вам предлагается написать программу для поиска простых множителей с заданным целым числом . Главными факторами числа являются все простые числа, которые будут точно делить данное число. Например, простые факторы 35 равны 7 и 5, оба являются простыми сами по себе и точно делят 35. В последний раз я делал это упражнение, когда учился в колледже, и это было что-то вроде написания программы, которая запрашивает у пользователя целочисленный ввод а затем отобразить начальную факторизацию этого числа в командной строке. Существуют также варианты этой программы, например, посмотрите на это упражнение. Напишите программу, которая предлагает пользователю ввести положительное целое число и отображает все его наименьшие коэффициенты в порядке убывания. Это более или менее похоже на ранее упомянутую версию первичной проблемы факторизации, но с уловом их отображения в порядке убывания. Отображение не является проблемой, вы можете легко отобразить его в командной строке или графическом интерфейсе, главное — написать логику для поиска основных факторов, и это то, что вы изучите в этом руководстве по программированию. Помните, мы не можем использовать метод API, который напрямую решает проблему, например, вам не разрешено использовать обратный метод StringBuffer , чтобы полностью изменить строку в Java. Вам необходимо написать основную логику простой факторизации, используя примитивные программные конструкции, например операторы управления, циклы, арифметический оператор и т. Д.
Java-программа для поиска основных факторов

Не откладывая дальше, здесь находится наша полная Java-программа для поиска основных факторов. Логика вычисления простых факторов записана внутри метода primeFactors (длинное число), это простая логика грубой силы для поиска простых факторов. Мы начинаем с 2, поскольку это первое простое число, и каждое число также делится на 1, затем мы выполняем итерацию до тех пор, пока не найдем простой множитель, увеличивая и шагая по одному. Когда мы находим простой фактор, мы храним его внутри набора, а также уменьшаем число, до которого мы зацикливаемся. Чтобы запустить эту программу, вы можете просто скопировать и вставить ее в файл PrimeFactors.java, а затем скомпилировать и запустить с помощью команд javac и java. Если вы обнаружите какие-либо трудности с запуском этой программы, вы также можете обратиться к этой статье за пошаговым руководством о том, как запустить программу на Java из командной строки .
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
|
import java.util.HashSet;import java.util.Random;import java.util.Scanner;import java.util.Set;/*** Java program to print prime factors of a number. For example if input is 15,* then it should print 3 and 5, similarly if input is 30, then it should* display 2, 3 and 5.** @author Javin Paul*/public class PrimeFactors{ public static void main(String args[]) { System.out.printf("Prime factors of number '%d' are : %s %n", 35, primeFactors(35)); System.out.printf("Prime factors of integer '%d' are : %s %n", 72, primeFactors(72)); System.out.printf("Prime factors of positive number '%d' is : %s %n", 189, primeFactors(189)); System.out.printf("Prime factors of number '%d' are as follows : %s %n", 232321, primeFactors(232321)); System.out.printf("Prime factors of number '%d' are as follows : %s %n", 67232321, primeFactors(67232321)); } /** * @return prime factors of a positive integer in Java. * @input 40 * @output 2, 5 */ public static Set primeFactors(long number) { long i; Set primefactors = new HashSet<>(); long copyOfInput = number; for (int i = 2; i <= copyOfInput; i++) { if (copyOfInput % i == 0) { primefactors.add(i); // prime factor copyOfInput /= i; i--; } } return primefactors; }}Output:Prime factors of number '35' are : [5, 7]Prime factors of integer '72' are : [2, 3]Prime factors of positive number '189' is : [3, 7]Prime factors of number '232321' are as follows : [4943, 47]Prime factors of number '67232321' are as follows : [12343, 419, 13] |
Если вам интересно, что это за угловая скобка <>, ее оператор Diamond введен в Java 7 для лучшего вывода типов. Теперь вам не нужно записывать параметры типа в обе стороны выражения, как в Java 1.6, это делает их более читабельными. Теперь возвращаясь к упражнению, если вы посмотрите на вывод, он возвращает только уникальные простые факторы, потому что мы используем интерфейс Set, который не допускает дублирования. Если ваш собеседник попросит вас написать программу для деления числа на его основные множители и распечатать все из них, то вам нужно использовать интерфейс List вместо Set. Например, уникальные простые множители ’72 ‘равны [2,3], но число в терминах его простого множителя составляет [2, 2, 2, 3, 3] . Если вам нужен такой вывод, вы можете переписать наш метод primeFactors (длинное число), чтобы вернуть List <Integer> , как показано ниже:
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
|
public static List<Integer> primeFactors(long number) { List<Integer> primefactors = new ArrayList<>(); long copyOfInput = number; for (int i = 2; i <= copyOfInput; i++) { if (copyOfInput % i == 0) { primefactors.add(i); // prime factor copyOfInput /= i; i--; } } return primefactors; } |
и вот результат запуска той же программы с этой версией метода primeFactors (длинное число) . На этот раз вы можете увидеть все основные факторы, а не только уникальные. Это также объясняет разницу между интерфейсом Set и List , очень важный урок для начинающих.
|
1
2
3
4
5
|
Prime factors of number '35' are : [5, 7] Prime factors of integer '72' are : [2, 2, 2, 3, 3] Prime factors of positive number '189' is : [3, 3, 3, 7] Prime factors of number '232321' are as follows : [47, 4943] Prime factors of number '67232321' are as follows : [13, 419, 12343] |
Теперь пришло время попрактиковаться в написании некоторых тестов JUnit. На самом деле есть два способа проверить ваш код, один из них — написать основной метод, вызвать метод и сравнить фактический результат с ожидаемым результатом самостоятельно. Другой, гораздо более продвинутый и предпочтительный подход — использовать для этого инфраструктуру модульного тестирования, например, JUnit. Если вы следите за разработкой, основанной на тестировании, вы даже можете написать тест перед написанием кода и позволить тесту управлять вашим дизайном и кодированием. Посмотрим, как поживает наша программа с тестированием JUnit.
|
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
import static org.junit.Assert.*;import java.util.ArrayList;import java.util.List;import org.junit.Test;public class PrimeFactorTest { private List<Integer> list(int... factors){ List<Integer> listOfFactors = new ArrayList<>(); for(int i : factors){ listOfFactors.add(i); } return listOfFactors; } @Test public void testOne() { assertEquals(list(), PrimeFactors.primeFactors(1)); } @Test public void testTwo() { assertEquals(list(2), PrimeFactors.primeFactors(2)); } @Test public void testThree() { assertEquals(list(3), PrimeFactors.primeFactors(3)); } @Test public void testFour() { assertEquals(list(2,2), PrimeFactors.primeFactors(4)); } @Test public void testSeventyTwo() { assertEquals(list(2,2,2,3,3), PrimeFactors.primeFactors(72)); }} |
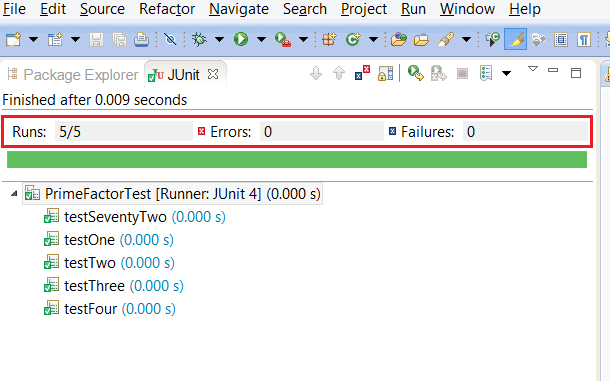
В нашем тестовом классе PrimeFactorsTest у нас есть пять тестовых случаев для тестирования угловых случаев, случаев с одним простым фактором и нескольких случаев с основным фактором. Мы также создали список служебных методов (int… ints), которые используют преимущества Java 5 для возврата списка заданных чисел. Вы можете вызывать этот метод с любым количеством аргументов, включая ноль, и в этом случае он вернет пустой список. Если хотите, вы можете расширить наш тестовый класс, добавив еще несколько тестов, например, тест производительности, или несколько тестов специального случая, чтобы протестировать наш основной алгоритм факторизации.
Вот результаты наших тестов JUnit. Если вы новичок, вы также можете посмотреть этот учебник, чтобы узнать, как создать и запустить тест JUnit .
Это все о том, как найти простые факторы целого числа в Java. Если вам нужна дополнительная практика, вы также можете проверить следующие 20 упражнений по программированию, начиная от различных тем, например, LinkdList, String, Array, Logic и Concurrency.
- Как поменять местами два числа без использования временной переменной в Java? ( Трюк )
- Как проверить, содержит ли LinkedList цикл в Java? ( Решение )
- Напишите программу для проверки, является ли число степенью двойки или нет? ( Ответ )
- Как найти средний элемент LinkedList за один проход? (Смотрите здесь для решения)
- Как проверить, является ли число премьер или нет? ( Решение )
- Написать программу, чтобы найти ряд Фибоначчи от заданного числа? ( Решение )
- Как проверить, является ли номер Армстронг номером или нет? ( Решение )
- Написать программу для предотвращения тупиков в Java? (Нажмите здесь для решения)
- Напишите программу для решения проблемы потребителей в Java. ( Решение )
- Как обратить String в Java без использования методов API? ( Решение )
- Написать программу для расчета факториала с использованием рекурсии в Java? (Нажмите здесь для решения)
- Как проверить, является ли число палиндромом или нет? ( Решение )
- Как проверить, содержит ли массив повторяющийся номер или нет? ( Решение )
- Как удалить дубликаты из ArrayList в Java? ( Решение )
- Напишите программу на Java, чтобы увидеть, являются ли две строки анаграммой друг друга? ( Решение )
- Как подсчитать вхождения персонажа в строку? ( Решение )
- Как найти первые неповторяющиеся символы из строки в Java? (Смотрите здесь для решения)
- Написать программу, чтобы проверить, является ли число двоичным в Java? ( Решение )
- Как удалить дубликаты из массива без использования Collection API? ( Решение )
- Написать программу для расчета суммы цифр числа в Java? ( Решение )
| Ссылка: | Как найти главные факторы целых чисел в Java — Факторизация от нашего партнера JCG Явина Пола в блоге Javarevisited . |