Недавно мне нужно было проверить ответы на домашние задания, связанные с использованием квадратной формулы . Поняв, что делать это вручную становится утомительно, я решил использовать свой калькулятор для их решения. Однако я понял, что могу написать простое приложение, использующее JavaFX для вычисления результатов, и этот подход кажется более интересным, чем использование калькулятора. Этот пост демонстрирует это простое приложение и предоставляет относительно простой код, необходимый для его реализации.
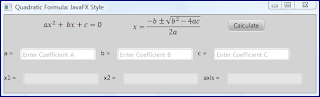
Следующая пара снимков экрана демонстрирует простое приложение на примере. Они включают в себя первоначальный вид приложения, а затем пару изображений, показывающих различные значения, рассчитанные приложением.
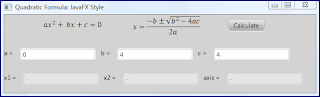
Последний снимок экрана показывает выходные данные, когда один из предоставленных коэффициентов не позволяет применить квадратную формулу. Чтобы предоставить этому приложению чуть более широкое применение, чем решение исключительно квадратного уравнения, я добавил код для определения, когда коэффициент «a» равен нулю, а коэффициент «b» не равен нулю. Это линейное уравнение, и простое приложение решает его так же, как и представленные квадратные уравнения. Следующий снимок экрана демонстрирует выходные данные, когда предоставляются коэффициенты для линейного уравнения.
Первый листинг кода не имеет ничего общего с уровнем представления JavaFX, но вместо этого представляет собой простой вызов, который обеспечивает вычисления базовой квадратной формулы. Я включил его сюда, потому что он используется примером приложения JavaFX. Это несколько интересно само по себе, потому что в Java существует множество способов вычисления квадратного корня. Наиболее известным подходом является использование Math.sqrt (double) , но варианты часто более разнообразны при использовании BigDecimal вместо double. Поскольку цель моего поста состоит в том, чтобы сосредоточиться на аспекте JavaFX и потому, что выбранный мной подход достаточно точен для своих целей, я выбрал «легкий путь» и просто использовал Math.sqrt (double).
SimplisticQuadraticFormula.java
package dustin.examples;
import java.math.BigDecimal;
import java.math.MathContext;
import java.math.RoundingMode;
import java.util.ArrayList;
import java.util.List;
/**
* Class encapsulating quadratic formula implementation.
*
* @author Dustin
*/
public class SimplisticQuadraticFormula
{
/** Default precision used for specifying scale. */
private static final int DEFAULT_PRECISION = MathContext.DECIMAL64.getPrecision();
/** Convenient representation of zero as BigDecimal. */
private static final BigDecimal ZERO = new BigDecimal("0");
/** Convenient representation of two as BigDecimal. */
private static final BigDecimal TWO = new BigDecimal("2");
/** Convenient representation of four as BigDecimal. */
private static final BigDecimal FOUR = new BigDecimal("4");
/**
* Calculate intercepts with x-axis.
*
* @param a Coefficient 'a' from a quadratic equation to be solved.
* @param b Coefficient 'b' from a quadratic equation to be solved.
* @param c Coefficient 'c' from a quadratic equation to be solved.
* @return The x-intercepts or solutions to the quadratic equation (two values)
* or a single value if solution to a linear equation. Note that two
* solutions are always provided for quadratic equations even if they are
* the same.
* @throws NumberFormatException Thrown when x-intercepts cannot be calculated.
*/
public static List<BigDecimal> calculateXIntercepts(
final BigDecimal a, final BigDecimal b, final BigDecimal c)
{
final List<BigDecimal> intercepts = new ArrayList<BigDecimal>();
if (a.compareTo(ZERO) == 0 && b.compareTo(ZERO) == 0)
{
// neither quadratic nor linear
throw new NumberFormatException("Must have coefficient for one of x terms.");
}
else if (a.compareTo(ZERO) == 0) // linear equation
{
intercepts.add(c.setScale(DEFAULT_PRECISION).negate().divide(b, RoundingMode.HALF_UP));
}
else
{
final BigDecimal intercept1 =
calculateNumeratorWithAddition(a, b, c)
.divide(calculateDenominator(a), RoundingMode.HALF_UP);
intercepts.add(intercept1);
final BigDecimal intercept2 =
calculateNumeratorWithSubtraction(a, b, c)
.divide(calculateDenominator(a), RoundingMode.HALF_DOWN);
intercepts.add(intercept2);
}
return intercepts;
}
/**
* Calculate axis of symmetry, if applicable.
*
* @param a Coefficient 'a' from a quadratic equation to be solved.
* @param b Coefficient 'b' from a quadratic equation to be solved.
* @return The "x" axis of symmetry.
* @throws NumberFormatException Thrown if the provided 'a' coefficient is
* zero because cannot divide by zero.
*/
public static BigDecimal calculateAxisOfSymmetry(final BigDecimal a, final BigDecimal b)
{
if (a.compareTo(ZERO) == 0)
{
throw new NumberFormatException(
"Cannot calculate axis of symmetry based on x-intercepts when a is zero.");
}
return b.setScale(DEFAULT_PRECISION).negate().divide(a.multiply(TWO), RoundingMode.HALF_UP);
}
/**
* Calculate numerator of quadratic formula where the terms are added.
*
* @param a Coefficient 'a' from a quadratic equation to be solved.
* @param b Coefficient 'b' from a quadratic equation to be solved.
* @param c Coefficient 'c' from a quadratic equation to be solved.
* @return Value of numerator in quadratic formula where terms are added.
* @throws NumberFormatException Thrown if no real solution is available.
*/
private static BigDecimal calculateNumeratorWithAddition(
final BigDecimal a, final BigDecimal b, final BigDecimal c)
{
return b.negate().add(calculateSquareRootPortion(a, b, c));
}
/**
* Calculate numerator of quadratic formula where the terms are subtracted.
*
* @param a Coefficient 'a' from a quadratic equation to be solved.
* @param b Coefficient 'b' from a quadratic equation to be solved.
* @param c Coefficient 'c' from a quadratic equation to be solved.
* @return Value of numerator in quadratic formula where terms are subtracted.
* @throws NumberFormatException Thrown if no real solution is available.
*/
private static BigDecimal calculateNumeratorWithSubtraction(
final BigDecimal a, final BigDecimal b, final BigDecimal c)
{
return b.negate().subtract(calculateSquareRootPortion(a, b, c));
}
/**
* Calculate denominator of quadratic formula.
*
* @param a Coefficient of 'a' from a quadratic equation to be solved.
* @return Value of denominator in quadratic formula.
* @throws NumberFormatException Thrown in 0 is provided for coefficient 'a'
* because denominator cannot be zero.
*/
private static BigDecimal calculateDenominator(final BigDecimal a)
{
if (a.compareTo(ZERO) == 0)
{
throw new NumberFormatException("Denominator cannot be zero.");
}
return a.multiply(TWO);
}
/**
* Calculates value of square root portion of quadratic formula.
*
* @param a Coefficient 'a' from a quadratic equation to be solved.
* @param b Coefficient 'b' from a quadratic equation to be solved.
* @param c Coefficient 'c' from a quadratic equation to be solved.
* @return The square root portion of the quadratic formula applied with
* the three provided co-efficients.
* @throws NumberFormatException Thrown if there is no solution (no
* intersection of the x-axis) or if a number is encountered that cannot
* be handled with BigDecmal return type.
*/
private static BigDecimal calculateSquareRootPortion(
final BigDecimal a, final BigDecimal b, final BigDecimal c)
{
BigDecimal sqrt;
final BigDecimal subtrahend = a.multiply(c).multiply(FOUR);
final BigDecimal insideSqrt = b.pow(2).subtract(subtrahend);
if (insideSqrt.compareTo(ZERO) < 0)
{
throw new NumberFormatException("Cannot be solved: no x-intercepts.");
}
else
{
final double value = insideSqrt.doubleValue();
final double sqrtDouble = Math.sqrt(value);
sqrt = new BigDecimal(sqrtDouble); // may throw NumberFormatException
}
return sqrt;
}
}
После того, как часть вычислений будет готова, пришло время перейти к этой теме (презентация через JavaFX 2). В следующем листинге кода представлен класс JavaFX 2 (написанный на чистом Java), используемый для приложения. Обратите внимание, что большая часть кода уровня представления могла быть написана с использованием FXML .
QuadraticCalculator.java
package dustin.examples;
import java.math.BigDecimal;
import java.util.List;
import javafx.application.Application;
import javafx.event.ActionEvent;
import javafx.event.EventHandler;
import javafx.geometry.Pos;
import javafx.scene.Group;
import javafx.scene.Scene;
import javafx.scene.control.Button;
import javafx.scene.control.Label;
import javafx.scene.control.TextField;
import javafx.scene.control.TextFieldBuilder;
import javafx.scene.image.Image;
import javafx.scene.image.ImageView;
import javafx.scene.layout.HBox;
import javafx.scene.layout.VBox;
import javafx.scene.paint.Color;
import javafx.stage.Stage;
/**
* JavaFX-based application for solving quadratic equations.
*
* @author Dustin
*/
public class QuadraticCalculator extends Application
{
/** Coefficient A used in quadratic formula. */
private TextField coefficientA =
TextFieldBuilder.create().promptText("Enter Coefficient A").build();
/** Coeffecient B used in quadratic forumal. */
private TextField coefficientB =
TextFieldBuilder.create().promptText("Enter Coefficient B").build();
/** Coeffecient C (constant) used in quadratic formula. */
private TextField coefficientC =
TextFieldBuilder.create().promptText("Enter Coefficient C").build();
/** First x-intercept. */
private TextField xIntercept1 =
TextFieldBuilder.create().disable(true).editable(false).build();
/** Second x-intercept. */
private TextField xIntercept2 =
TextFieldBuilder.create().disable(true).editable(false).build();
/** Axis of symmetry. */
private TextField symmetryAxis =
TextFieldBuilder.create().disable(true).editable(false).build();
/**
* Extract Image with provided name.
*
* @param imageName Name of image to be provided.
* @return Loaded image.
*/
private Image getImage(final String imageName)
{
final String jarFileUrl =
this.getClass().getProtectionDomain().getCodeSource().getLocation().toString();
final String url = "jar:" + jarFileUrl + "!/" + imageName;
System.out.println(url);
return new Image(url, true);
}
/**
* Provide a read-only horizontal box with quadratic equation and quadratic
* formula and with a button that can be clicked to calculate solution to
* quadration equation with provided coefficients.
*
* @return Horizontal box with quadratic equation and quadratic formula.
*/
private HBox buildEquationsBox()
{
final HBox equationsBox = new HBox();
equationsBox.setAlignment(Pos.CENTER);
equationsBox.setSpacing(50);
final Image quadraticEquation = getImage("quadraticEquation-transparent.png");
final ImageView equationView = new ImageView(quadraticEquation);
equationsBox.getChildren().add(equationView);
final Image quadraticFormula = getImage("quadraticFormula-transparent.png");
final ImageView formulaView = new ImageView(quadraticFormula);
equationsBox.getChildren().add(formulaView);
final Button calculateButton = new Button("Calculate");
calculateButton.setOnAction(
new EventHandler<ActionEvent>()
{
public void handle(ActionEvent t)
{
final BigDecimal a = extractBigDecimal(coefficientA.getText());
final BigDecimal b = extractBigDecimal(coefficientB.getText());
final BigDecimal c = extractBigDecimal(coefficientC.getText());
try
{
final List<BigDecimal> intercepts =
SimplisticQuadraticFormula.calculateXIntercepts(a, b, c);
xIntercept1.setText(intercepts.get(0).toPlainString());
xIntercept1.setDisable(false);
if (intercepts.size() > 1)
{
xIntercept2.setText(intercepts.get(1).toEngineeringString());
xIntercept2.setDisable(false);
}
else
{
xIntercept2.setText("-");
xIntercept2.setDisable(true);
}
if (a.compareTo(new BigDecimal("0")) != 0)
{
final BigDecimal axis =
SimplisticQuadraticFormula.calculateAxisOfSymmetry(a, b);
symmetryAxis.setText(axis.toPlainString());
symmetryAxis.setDisable(false);
}
else
{
symmetryAxis.setText("-");
symmetryAxis.setDisable(true);
}
}
catch (NumberFormatException nfe)
{
xIntercept1.setText("-");
xIntercept1.setDisable(true);
xIntercept2.setText("-");
xIntercept2.setDisable(true);
symmetryAxis.setText("-");
symmetryAxis.setDisable(true);
}
}
});
equationsBox.getChildren().add(calculateButton);
return equationsBox;
}
/**
* Converts provided String to BigDecimal.
*
* @param possibleNumber String to be converted to an instance of BigDecimal.
* @return The BigDecimal corresponding to the provided String or Double.NaN
* if the conversion cannot be performed.
*/
private BigDecimal extractBigDecimal(final String possibleNumber)
{
BigDecimal extractedNumber;
try
{
extractedNumber = new BigDecimal(possibleNumber);
}
catch (NumberFormatException nfe)
{
extractedNumber = null;
}
return extractedNumber;
}
/**
* Provide horizontal box with labels of coefficients and fields to enter
* coefficient values.
*
* @return Horizontal box for entering coefficients.
*/
private HBox buildEntryBox()
{
final HBox entryBox = new HBox();
entryBox.setSpacing(10);
final Label aCoeff = new Label("a = ");
entryBox.getChildren().add(aCoeff);
entryBox.getChildren().add(this.coefficientA);
final Label bCoeff = new Label("b = ");
entryBox.getChildren().add(bCoeff);
entryBox.getChildren().add(this.coefficientB);
final Label cCoeff = new Label("c = ");
entryBox.getChildren().add(cCoeff);
entryBox.getChildren().add(this.coefficientC);
return entryBox;
}
/**
* Construct the output box with solutions based on quadratic formula.
*
* @return Output box with solutions of applying quadratic formula given
* provided input coefficients.
*/
private HBox buildOutputBox()
{
final HBox outputBox = new HBox();
outputBox.setSpacing(10);
final Label x1 = new Label("x1 = ");
outputBox.getChildren().add(x1);
outputBox.getChildren().add(this.xIntercept1);
final Label x2 = new Label("x2 = ");
outputBox.getChildren().add(x2);
outputBox.getChildren().add(this.xIntercept2);
final Label axis = new Label("axis = ");
outputBox.getChildren().add(axis);
outputBox.getChildren().add(this.symmetryAxis);
return outputBox;
}
/**
* Build overall presentation of application.
*
* @return Vertical box representing input and output of application.
*/
private VBox buildOverallVerticalLayout()
{
final VBox vbox = new VBox();
vbox.setSpacing(25);
vbox.getChildren().add(buildEquationsBox());
vbox.getChildren().add(buildEntryBox());
vbox.getChildren().add(buildOutputBox());
vbox.setAlignment(Pos.CENTER);
return vbox;
}
/**
* Start the JavaFX application for solving quadratic equations.
*
* @param stage Primary stage.
* @throws Exception JavaFX-related exception.
*/
@Override
public void start(final Stage stage) throws Exception
{
final Group groupRoot = new Group();
groupRoot.getChildren().add(buildOverallVerticalLayout());
final Scene scene = new Scene(groupRoot, 600, 150, Color.LIGHTGRAY);
stage.setTitle("Quadratic Formula: JavaFX Style");
stage.setScene(scene);
stage.show();
}
/**
* Main function for running the JavaFX-based quadratic equation solver.
*
* @param arguments
*/
public static void main(final String[] arguments)
{
Application.launch(arguments);
}
}
Приведенный выше код JavaFX 2 загружает два изображения с прозрачным фоном для отображения стандартной формы квадратного уравнения и отображения квадратной формулы. В предыдущем посте я загружал эти изображения с внешнего URL-адреса, но в этом примере я загружал их из JAR-файла приложения. Эти изображения отображаются рядом независимо от приложения.
квадратное уравнение-transparent.png
quadraticFormula-transparent.png
Есть несколько способов улучшить это упрощенное приложение. Одним из улучшений было бы сделать размеры регулируемыми и связанными друг с другом, чтобы окно можно было перетаскивать больше или меньше и при этом выглядело хорошо. Еще одним улучшением будет предоставление какого-либо сообщения о состоянии на интерфейсе, особенно в ситуациях, когда решения не могут быть рассчитаны. Третье усовершенствование заключается в представлении графика квадратного уравнения, заданного с помощью предоставленных коэффициентов, для визуального указания пересечений x и оси симметрии.
JavaFX 2 позволяет довольно просто писать простые и удобные приложения.
От http://marxsoftware.blogspot.com/2012/01/javafx-2-presents-quadratic-formula.html