Статьи

Геометрическое броуновское движение с Java

Февраль 6, 2019

Процесс Винера — это непрерывный случайный процесс, названный в честь Норберта Винера. Это обычно используется, чтобы представить шум или финансовое развитие со случайным компонентом.

Геометрическое броуновское движение может быть рассчитано для визуализации определенных границ (в квантилях) для намека на абсолютный диапазон. Для расчета необходимы следующие параметры:

  • µ (mu): средний процент
  • σ (сигма): дисперсия
  • t: период времени
  • v: начальное значение

В расширении регулярного расчета используются: m: увеличение значения за период времени (в моем случае месячное значение) разрывы: квантильные разрывы для расчета границ

Код для расчета значений:

01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
import java.time.LocalDate;
import java.util.*;
import static java.lang.Math.sqrt;
import static java.lang.Math.exp;
 
public class WienerProcess {
    /**
     * Run the Wiener process for a given period and initial amount with a monthly value that is added every month. The
     * code calculates the projection of the value, a set of quantiles and the brownian geometric motion based on a
     * random walk.
     *
     * @param mu mean value (annualized)
     * @param sigma standard deviation (annualized)
     * @param years projection duration in years
     * @param initialValue the initial value
     * @param monthlyValue the value that is added per month
     * @param breaks quantile breaks
     * @return a List of double arrays containing the values per month for the given quantile breaks
     */
    public static List<double[]> getProjection(double mu, double sigma, int years, int initialValue,
        int monthlyValue, double[] breaks) {
        double periodizedMu = mu / 12;
        double periodizedSigma = sigma / Math.sqrt(12);
        int periods = years * 12;
 
        List<double[]> result = new ArrayList<double[]>();
 
        for (int i = 0; i < periods; i++) {
            double value = initialValue + (monthlyValue * i);
            NormalDistribution normalDistribution = new NormalDistribution(periodizedMu * (i + 1),
                    periodizedSigma * sqrt(i + 1));
            double bounds[] = new double[breaks.length];
            for (int j = 0; j < breaks.length; j++) {
                double normInv = normalDistribution.inverseCumulativeProbability(breaks[j]);
                bounds[j] = value * exp(normInv);
            }
 
            result.add(bounds);
        }
        return result;
    }
}

Применение значений:

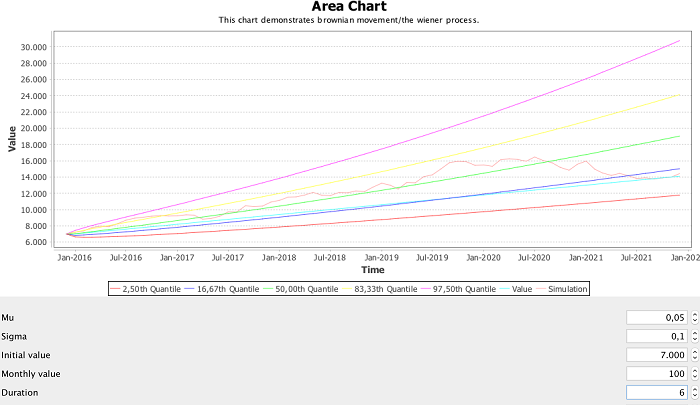
  • мю: 0,05 (или 5%)
  • сигма: 0,1 (или 10%)
  • начальное значение: 7000
  • ежемесячное увеличение: 100
  • период времени: 6 лет

результаты в следующем графике:

Fig1_50593

Связанная информация

Ссылка: Геометрическое броуновское движение с Java от нашего партнера JCG Марка Палуха в блоге paluch.biz .
40
Share: