Если Хемингуэй написал JavaScript: объяснил

Я написал книгу под названием « Если Хемингуэй написал JavaScript», в которой я представляю 25 известных писателей, поэтов и драматургов, решающих простые задачи на JavaScript. Это отчасти дань уважения моим любимым писателям и отчасти любовное письмо к JavaScript, единственному языку, который я знаю с достаточной свободой, творческим потенциалом и откровенным изворотливостью, чтобы вызвать интерес литературных великих людей.

Этот пост содержит оригинальный материал, которого нет в книге (представьте, что это одна из тех бонусов «за кадром»). Это первое из серии глубоких технических погружений в решение каждого автора. Некоторые решения требуют большего объяснения, чем другие.

Наслаждайтесь!

Часть 1: простые числа

1. Хорхе Луис Борхес
2. Льюис Кэрролл
3. Дуглас Адамс
4. Чарльз Диккенс
5. Дэвид Фостер Уоллес
6. Заключение / О книге

Назначение: напишите функцию, которая возвращает все простые числа вплоть до значения предоставленного аргумента.

1. Хорхе Луис Борхес

https://github.com/angus-c/literary.js/tree/master/book/borges/prime.js

// They speak (I know) of finials, newels and balustrades
// of hidden spandrels and eternally clambering, broad-gaited beasts...
 
var monstersAscendingAStaircase = function(numberOfSteps) {
  var stairs = []; stepsUntrodden = [];
  var largestGait = Math.sqrt(numberOfSteps);
 
  // A succession of creatures mount the stairs;
  // each creature's stride exceeds that of its predecessor
  for (var i = 2; i <= largestGait; i++) {
    if (!stairs[i]) {
      for (var j = i * i; j <= numberOfSteps; j += i) {
        stairs[j] = "stomp";
      }
    }
  }
 
  // Long-limbed monsters won't tread on prime numbered stairs.
  for (var i = 2; i <= numberOfSteps; i++) {
    if(!stairs[i]) {
      stepsUntrodden.push(i);
    }
  }
 
  // Here, then, is our answer.
  return stepsUntrodden;
};

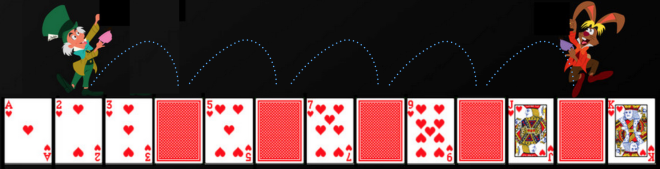
Решение Борхеса — это разновидность алгоритма Сита Эратосфена , с помощью которого кратные каждого известного простого числа помечаются как составные (не простые). В этом случае Борхес уже давно монстры на ногах займет место делителей. Каждый монстр простирается на одну ступеньку выше, чем монстр, который был раньше: 2, 3, 4, 5… до квадратного корня числа самой высокой ступени. (по неочевидным причинам Borges позволяет монстрам со сложными движениями подниматься по лестнице). Не пройденные ступени — это простые числа.

Обратите внимание на строку 12, что каждый монстр начинает свое восхождение от квадрата фактора:

for (var j = i * i; j <= numberOfSteps; j += i) {

Это потому, что композиты между n и n² уже будут протоптаны монстрами с меньшими шагами.

2. Льюис Кэрролл

https://github.com/angus-c/literary.js/tree/master/book/carroll/prime.js

function downTheRabbitHole(growThisBig) {
  var theFullDeck = Array(growThisBig);
  var theHatter = Function('return this/4').call(2*2);
  var theMarchHare = Boolean('The frumious Bandersnatch!');
 
  var theVerdict = 'the white rabbit'.split(/the march hare/).slice(theHatter);
 
  //into the pool of tears...
  eval(theFullDeck.join('if (!theFullDeck[++theHatter]) {\
      theMarchHare = 1;\
      theVerdict.push(theHatter);\
      ' + theFullDeck.join('theFullDeck[++theMarchHare * theHatter]=true;') + '}')
  );
 
  return theVerdict;
}

Как и в его письме, большая часть решения Кэрролла — либо загадка, либо бессмыслица. Давайте расшифруем его построчно, начиная с объявления переменных.

Строка 2 на самом деле довольно условна (если мы пропускаем использование конструктора Array). Кэрролл создает пустой массив, длина которого соответствует указанному аргументу. Он называется theFullDeck, потому что его решение представляет собой колоду игральных карт, для которой в конце останутся только простые числа.

Строка 3 создает функцию (используя малоиспользуемый конструктор Function), а затем вызывает ее с помощью вызова, передавая 2 * 2 (т.е. 4) в качестве аргумента this. Таким образом, Шляпник инициализируется 1.

Строка 4 устанавливает theMarchHare в значение true. Когда булев конструктор вызывается как функция, он преобразует свой аргумент в true или false. В этом случае непустая строка ‘Frumious Bandersnatch!’ преобразуется в истину. (Заметьте, кстати, что это назначение совершенно не нужно, потому что новое значение назначено theMarchHare в строке 10).

Наконец, и, возможно, самый нелепый, в строке 6 Кэрролл назначает пустой вердикт совершенно определенным образом:

var theVerdict = 'the white rabbit'.split(/the march hare/).slice(theHatter);

Здесь на самом деле меньше, чем кажется на первый взгляд. Аргумент для разделения — это регулярное выражение, которое не соответствует «белому кролику», поэтому при вызове этого разбиения получается массив, содержащий только «белого кролика». Последующая операция среза заполняет копию массива всеми элементами исходного массива, начиная с предоставленного индекса. Поскольку наш одноэлементный массив не имеет индекса 1 (значение theHatter), из него не копируются никакие члены, и в результате получается пустой массив.

Упрощенно, мы могли бы переписать объявления переменных следующим образом:

function downTheRabbitHole(growThisBig) {
  var theFullDeck = Array(growThisBig);
  var theHatter = 1;
  var theMarchHare = true;
  var theVerdict = [];

Теперь к действительно дурацкой части:

//into the pool of tears...
eval(theFullDeck.join('if (!theFullDeck[++theHatter]) {\
    theMarchHare = 1;\
    theVerdict.push(theHatter);\
    ' + theFullDeck.join('theFullDeck[++theMarchHare * theHatter]=true;') + '}')
);

Прежде чем мы перейдем к сильно искаженной функции eval, давайте сосредоточимся на вложенных операторах соединения. Функция join превращает массив в строку, используя ее аргумент в качестве клея между каждым членом массива. Вызов соединения через пустой массив приводит к строке, состоящей полностью из клея (повторяется n — 1 раз, где n — длина массива):

Array(4).join('hi'); //'hihihi'

Если мы вложим два соединения, то будут вложены соответствующие клеи:

Array(4).join('A' + Array(4).join('a')); //'AaaaAaaaAaaa'

Включив переменные в клей, мы можем начать умничать:

var arr = [], count = 0;
Array(4).join('arr.push(' + Array(4).join('count++,') + '-1);');
//"arr.push(count++,count++,count++,-1);arr.push(count++,count++,count++,-1);arr.push(count++,count++,count++,-1)"

Теперь, когда мы научили JavaScript, как генерировать JavaScript, нам просто нужен способ его запустить. Введите подлого Eval …

var arr = [], count = 0;
eval(Array(4).join('arr.push(' + Array(4).join('count++,') + '-1);'));
arr; //[0, 1, 2, -1, 3, 4, 5, -1, 6, 7, 8, -1]

… И это стратегия, которую Кэрролл использует для автоматической генерации программы простых чисел. Давайте еще раз посмотрим на его код:

//into the pool of tears...
eval(theFullDeck.join('if (!theFullDeck[++theHatter]) {\
    theMarchHare = 1;\
    theVerdict.push(theHatter);\
    ' + theFullDeck.join('theFullDeck[++theMarchHare * theHatter]=true;') + '}')
);

Аргумент для eval разрешается (после форматирования):

if (!theFullDeck[++theHatter]) {
  theMarchHare = 1;
  theVerdict.push(theHatter);
  theFullDeck[++theMarchHare * theHatter] = true;
  theFullDeck[++theMarchHare * theHatter] = true;
  theFullDeck[++theMarchHare * theHatter] = true;
}
if (!theFullDeck[++theHatter]) {
  theMarchHare = 1;
  theVerdict.push(theHatter);
  theFullDeck[++theMarchHare * theHatter] = true;
  theFullDeck[++theMarchHare * theHatter] = true;
  theFullDeck[++theMarchHare * theHatter] = true;
}
if (!theFullDeck[++theHatter]) {
  theMarchHare = 1;
  theVerdict.push(theHatter);
  theFullDeck[++theMarchHare * theHatter] = true;
  theFullDeck[++theMarchHare * theHatter] = true;
  theFullDeck[++theMarchHare * theHatter] = true;
}
// etc...

…и так далее. (Этот сгенерированный код может быть очень длинным. Запрос на все простые числа до 100 генерирует более 10000 строк кода — с очевидными последствиями для производительности — но мы в Стране Чудес, так что все в порядке. Я думаю.)

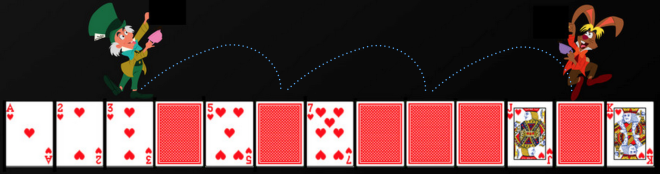
Anyway, gradually the mists are clearing. It turns out Carroll is applying a flavor of the same Sieve of Eratosthenes algorithm that was used by Borges. theFullDeck is an array representing every number to be tested, theHatter and theMarchHare are nested counters that are multiplied on every increment so as to generate every possible composite number. At the index of each composite number, the card is turned over (i.e. theFullDeck at that index is marked true). The remaining face-up cards are the primes.

3. Douglas Adams

https://github.com/angus-c/literary.js/tree/master/book/adams/prime.js

// Here I am, brain the size of a planet, and they ask me to write JavaScript...
function kevinTheNumberMentioner(_){
  l=[]
  /* mostly harmless --> */ with(l) {
 
    // sorry about all this, my babel fish has a headache today...
    for (ll=!+[]+!![];ll<_+(+!![]);ll++) {
      lll=+!![];
      while(ll%++lll);
      // I've got this terrible pain in all the semicolons down my right hand side
      (ll==lll)&&push(ll);
    }
    forEach(alert);
  }
 
  // you're really not going to like this...
  return [!+[]+!+[]+!+[]+!+[]]+[!+[]+!+[]];
}

Most of Adams’ solution is hard to read because the syntax borrows heavily from jsfuck, an ingenious yet upsetting little language that uses just 6 characters. Nevertheless it’s also valid JavaScript—if you run it in your console, it works. Let’s translate a short snippet:

for (ll=!+[]+!![];ll<_+(+!![]);ll++) {

This is a for loop and ll and _ are the names of variables. Everything else is literal and figurative brainfuck.

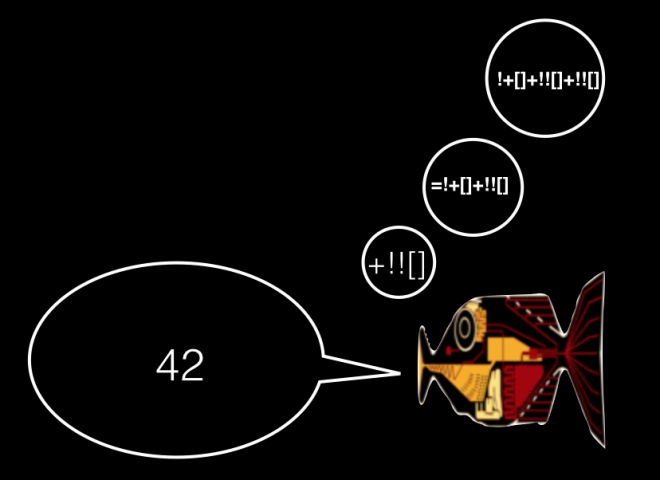
In the first clause of the statement, ll is assigned the value !+[]+!![]. Deconstructing that expression we can see there are two empty array literals. The first array literal is preceded by a + which coerces it to the number 0. Right before that there’s a ! which coerces the 0 to its boolean opposite, i.e., true. So !+[] resolves to true.

Now let’s look at the second array literal. It’s preceded by two !!s which will simply coerce it to a Boolean. Because arrays are always objects, the Boolean of an array is always true (see es5’s ToBoolean). So !![] also resolves to true.

Putting those two expressions together, !+[]+!![] is equivalent to true + true. Here the + coerces both operands to the number 1 so the expression ultimately resolves to 2.

The other two clauses of the for loop are now relatively easy to figure out. Again we see !![], this time preceded by a + which coerces true to 1. So ll<_+(+!![]) resolves to ll < _ + 1.

The final clause reads as a regular JavaScript postfix and so the entire for loop resolves to:

for (ll = 2; ll < _ + 1; ll++) {

Here’s the entire solution translated into regular earthling JavaScript. (I’ve also given the variables more meaningful names.)

// Here I am, brain the size of a planet, and they ask me to write JavaScript...
function kevinTheNumberMentioner(max){
  var result = [];
  /* mostly harmless --> */ with(result) {
 
    // sorry about all this, my babel fish has a headache today...
    for (candidate = 2; candidate < max + 1; candidate++) {
      var factor = 1;
      while (candidate % ++factor);
      // I've got this terrible pain in all the semicolons down my right hand side
      (candidate == factor) && push(candidate);
    }
    forEach(alert);
  }
 
  // you're really not going to like this...
  return '42';
}

OK, so now it’s recognizable JavaScript at least, but there are a number of lingering oddities.

The with statement is one of those language features that the JavaScript Police frown upon, and yet there’s one right there on line 3. JavaScript will attempt to scope all unreferenced properties within the with block to the given object. Thus the disturbingly orphaned array methods push and forEach will be scoped to result.

Another curious statement is the while loop on line 9. The loop has no body, so factor just keeps incrementing until it divides exactly into the candidate number. The next line checks if candidate now has the same value as factor. If it does, the number has no lesser factors so must be prime, and it’s added to result.

Line 13 loops through the result and shouts out each prime number in the form of an alert. Finally the program returns 42.

4. Charles Dickens

https://github.com/angus-c/literary.js/tree/master/book/dickens/prime.js

function MrsPrimmerwicksProgeny(MaxwellNumberby) {
  Number.prototype.isAPrimmerwick = function() {
    for (var AddableChopper = 2; AddableChopper <= this; AddableChopper++) {
      var BittyRemnant = this % AddableChopper;
      if (BittyRemnant == 0 && this != AddableChopper) {
        return console.log(
          'It is a composite. The dear, gentle, patient, noble', +this, 'is a composite'),
          false;
      }
    }
    return console.log(
      'Oh', +this, +this, +this, 'what a happy day this is for you and me!'),
      true;
  }
 
  var VenerableHeap = [];
  for (var AveryNumberby = 2; AveryNumberby <= MaxwellNumberby; AveryNumberby++) {
    if (AveryNumberby.isAPrimmerwick()) {
      VenerableHeap.push(AveryNumberby);
    }
  }
  return VenerableHeap;
}

Imagine if you could just ask a number if it’s a prime:

6..isPrime(); //false
7..isPrime(); //true

By extending Number.prototype that’s exactly what Charles Dickens does. His custom extension is called isAPrimmerwick (and in fact all his objects have quirky Dickensian names) and it’s defined on lines 2-14. Lines 17-21 simply ask each number if it’s a prime, and adds those that are to the results array which is called VenerableHeap.

The logic of the isAPrimmerwick method is mostly straightforward. The number in question is divided by each possible factor. If any division yields a zero remainder then the number is deemed composite (non-prime), else it’s a prime.

There are a couple of curiosities in each return statement (lines 6 and 11). First, since the number is calling a method on its own prototype, it can be referenced by this (but with a prefixed + to coerce it from a Number object to a primitive). Second, Dickens uses the comma operator to simultaneously invoke console.log and return a Boolean value.

5. David Foster Wallace

https://github.com/angus-c/literary.js/tree/master/book/wallace/prime.js

var yearOfTheLighteningQuickAtkinSieve = function(tops) {
  //B.P. #40 07-14
  //ELEPHANT BUTTE, NM
  var NSRS/*[1]*/ = [0,0,2,3];
  /* Two concurrent loops are mobilized such that the variables i and j (each having an
  initial value of 1) are incremented by steps of 1 (though in a nested fashion). */
  for(var i = 1; i < Math.sqrt(tops); i++){
    for(var j = 1; j < Math.sqrt(tops); j++){
      if (i*i + j*j >= tops) {
        break;
      }
      /* The two variables (i.e. i and j) are injected into the first quadratic,
      the result being assigned to the additional variable (n). */
      var n = 4*i*i + j*j;
      /* Should the additional variable (i.e. n) yield, when divided by 12, a remainder
      of 1 or 5, the value at that index (i.e. n's) is flipped [2]. */
      if(n <= tops && (n%12 == 1 || n%12 == 5)){
        NSRS[n] = NSRS[n] ? 0 : n;
      }
      /* Now, we (i.e. JavaScript) reach the second quadratic and again the result
      is assigned to the (existing) variable n. */
      n = 3*i*i + j*j;
      /* Although the variable (i.e. n) is again divided by 12, this time the remainder is
      checked against 7 to determine whether the indexed value (i.e. the value at n) needs
      flipping. */
      if(n <= tops && (n % 12 == 7)){
        NSRS[n] = NSRS[n] ? 0 : n;
      }
      /* By now you (i.e. the reader) are no doubt experiencing feelings of ambivalence and
      regret, nevertheless, we (i.e. JavaScript) haven't finished yet. Predictably, a third
      quadratic is now run and (equally predictably) it's value assigned to the (now
      world weary) variable, n. */
      n = 3*i*i - j*j;
      /* The only interesting thing about the third division (though also the depressing
      thing) is that it only happens when the first looping variable (i) is greater than
      i.e. not less than (or equal to) the second looping variable (j) [3]. */
      if (i>j) {
        if((n <= tops) && (n % 12 == 11)){
          NSRS[n] = NSRS[n] ? 0 : n;
        }
      }
    }
  }
  /* Near exhaustion (yet distrustful of the quadratic wheel factorization filter) we
  (i.e. JavaScript) now designate any and all prime factors, w/o regard for their current prime,
  or composite (i.e. non-prime) designation, as being composite (i.e non-prime) */
  for(i = 5; i < Math.sqrt(tops); i++){
    if(NSRS[i] == 1){
      for(j = i*i; j < tops; j += i*i){
        NSRS[j] = 0;
      }
    }
  }
  return NSRS.filter(Number); // [4]
}
/*
[1] Numeric Storage and Retrieval System.
[2] Meaning values representing the current index [a] are set to 0, while values of 0 are set to the
current index.
[3] Otherwise each relevant index [a] would be flipped twice.
[4] `Array.prototype.filter` being a higher order function defined by The EcmaScript-262 Standard (5th
edition) [b]. Since `Number` is a built-in function that converts any value to a number and Array.prototype.filter
rejects falsey (i.e. not truthy) values, thus values of 0, being falsey (i.e. not truthy) will
not be included in the array returned by `Array.prototype.filter`.
 
[a] i.e. an index for which the quadratic in question resolves to true.
[b] http://es5.github.io/#x15.4.4.20
*/

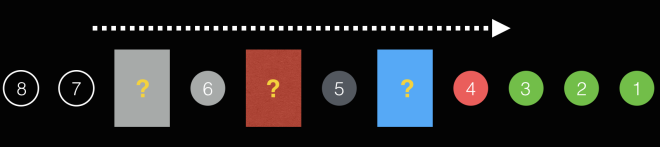
Thanks to Wallace’s famously abundant commentary, there’s not much left for me to describe here–except to say that his solution is based on the highly optimized (and too complicated to explain here) Sieve of Atkin (Wallace’s solution in particular owes a lot to this gist by Mohammad Shahrizal Prabowo).

The code is most notable for the elaborate logic and Wallace’s precise yet conversational annotation, but there’s also JavaScript interest down on line 54:

return NSRS.filter(Number); // [4]

NSRS is the result. At this point it’s a sparse array containing all the prime numbers, but interleaved with undefined values (and front-buffered with zeros):

[0, 0, 2, 3, undefined, 5, undefined, 7/*, etc.. */]

Array.prototype.filter creates a new array containing only those members of the original array for which the given function returns a truthy value. In this case the given function is Number, a built-in function that attempts to coerce its argument to a number. Number coerces undefined to NaN while leaving all genuine numbers untouched. Since both NaN and 0 are falsey values, the new array will contain only prime numbers:

[0, 0, 2, 3, undefined, 5, undefined, 7].filter(Number); //[2, 3, 5, 7]

Wrap Up / About the Book

And that’s that for Part 1. Hope you had fun and if you had any questions or notice any mistakes, feel free to add a comment, or tweet me at @angustweets

If you’ve enjoyed this or any of my previous posts on this site, consider buying a copy of If Hemingway Wrote JavScript. It’s beautifully designed and printed, and each of the twenty-five sections includes an original biography of the author, their imagined JavaScript solution, a code review and a gorgeous illustration by Miran Lipovača (of Learn Yourself a Haskell fame). Thanks!