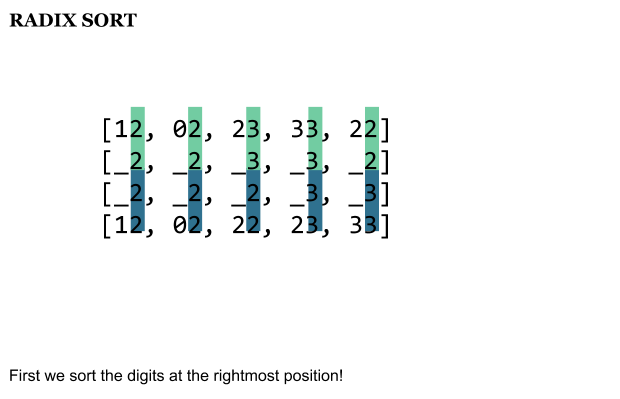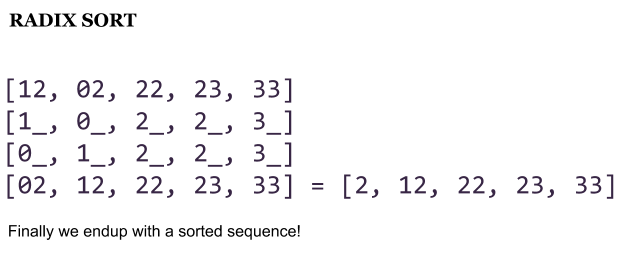Radix Sort
Первый вопрос, который мы задаем, когда видим фразу «сортировка по линейному времени», должен звучать так: «В чем подвох?» На самом деле есть подвох. Мы не можем ничего сортировать за линейное время. Большую часть времени мы можем говорить о сортировке целых чисел в линейном времени, но, как мы увидим позже, это не единственный случай.
Поскольку мы говорим о целых числах, мы можем придумать более быстрый алгоритм сортировки, чем обычно. Такой алгоритм является сортировкой счета, которая в некоторых случаях может быть очень быстрой, а в других — очень медленной, поэтому ее можно использовать осторожно. Другим линейным алгоритмом сортировки по времени является радикальная сортировка.
Вступление
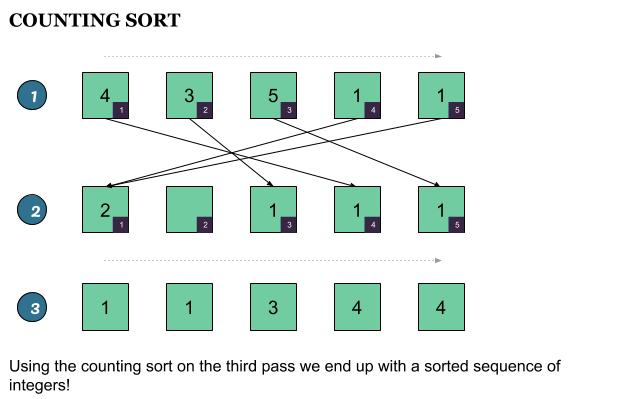
Сортировка графа абсолютно блестящая и простая в реализации. В случае, если мы сортируем целые числа в диапазоне [n, m] на первом проходе, мы просто инициализируем заполненный нулями массив с длиной mn. Чем на втором проходе мы «посчитаем» вхождение каждого целого числа. На третьем проходе мы просто с легкостью сортируем целые числа.
Однако у нас есть некоторые проблемы с этим алгоритмом. Что делать, если у нас есть только несколько предметов для сортировки, которые очень далеко друг от друга, как [2, 1, 10000000, 2]. Это приведет к очень большим неиспользованным данным. Итак, нам нужна плотная целочисленная последовательность. Это важно, потому что мы должны заранее знать природу последовательности, которая редко бывает достоверной.
Вот почему нам нужно использовать другой алгоритм линейной сортировки по времени для целых чисел, который не имеет этого недостатка. Такой алгоритм является радикальной сортировкой.
обзор
Идея, лежащая в основе сортировки radix, проста. Мы должны смотреть на нашу «целочисленную» последовательность как последовательность строк. Хорошо, чтобы прояснить ситуацию, приведу пример. Наша последовательность [12, 2, 23, 33, 22]. Сначала мы берем самую левую цифру каждого числа. Таким образом, мы должны сравнить [_2, 2, _3, _3, _2]. Ясно, что мы можем предположить, что поскольку второе число «2» представляет собой только однозначное число, мы можем заполнить его начальным «0», чтобы в нашем примере оно стало 02 или _2: [_2, _2, _3, _3, _2] , Теперь мы сортируем эту последовательность с помощью алгоритма стабильной сортировки.
Что такое алгоритм стабильной сортировки
Алгоритм стабильной сортировки — это алгоритм, который сортирует список, сохраняя позиции элементов в случае, если они равны. С точки зрения PHP это означает, что:
array(0 => 12, 1=> 13, 2 => 12); |
Будут отсортированы следующим образом:
array(0 => 12, 2 => 12, 1 => 13); |
Таким образом, третий элемент становится вторым после первого элемента. Обратите внимание, что третий и первый элемент равны, но третий появляется позже в последовательности, поэтому он остается позже в отсортированной последовательности.
В примере радикальной сортировки нам нужен стабильный алгоритм сортировки, потому что нам нужно беспокоиться только об одной позиции цифры, которую мы исследуем.
Так что же происходит в нашем примере после сортировки последовательности?
Как мы видим, мы далеки от сортированной последовательности, но что если мы перейдем к следующей «позиции» — десятичной цифре?
Чем мы закончим с этим:
Теперь у нас есть отсортированная последовательность, поэтому давайте обобщим алгоритм в коротком псевдокоде.
Псевдокод
Простой подход к алгоритму сортировки по основанию можно описать как псевдокод, предполагая, что мы сортируем десятичные целые числа.
1. Для каждой цифры в позиции от 10 ^ 0 до 10 ^ n
1.1. Сортировать числа по этой цифре, используя алгоритм стабильной сортировки;
Дело в том, что здесь мы говорим о десятичной дроби, но на самом деле этот алгоритм может применяться одинаково на любых числовых системах. Вот почему это называется «радикс».
Таким образом, мы можем сортировать двоичные числа, шестнадцатеричные числа и т. Д.
Важно отметить, что этот алгоритм может также использоваться для сортировки строк по алфавиту.
[ABC, BBC, ABA, AC] [__C, __C, __A, __C] => [ABA, ABC, BBC, AC] [_B_, _B_, _B_, _A_] => [AC, ABA, ABC, BBC] [___, A__, A__, B__] => [AC, ABA, ABC, BBC]
Это просто правильно, потому что мы можем предположить, что наш алфавит — это еще одна 27-значная цифровая система (в случае латинского алфавита).
сложность
Как я уже сказал в начале, основа сортировки — это алгоритм линейной сортировки по времени. Посмотрим почему. Сначала мы зависим от числовой системы. Давайте предположим, что у нас есть десятичная числовая система — тогда у нас есть N проходов, сортирующих 10 цифр, что просто 10 * N. В случае числовой системы K цифр наш алгоритм будет O (K * N), который является линейным.
Однако вы должны заметить, что в случае, если мы отсортируем N чисел в числовой системе из N цифр, сложность станет O (N ^ 2)!
Мы также должны помнить, что для реализации радикальной сортировки и поддерживающего алгоритма стабильной сортировки нам нужно дополнительное пространство.
заявка
Сортировка целых чисел может быть быстрее, чем сортировка чего угодно, поэтому в любое время, когда нам нужно реализовать алгоритм сортировки, мы должны тщательно исследовать входные данные. И это также большой недостаток этого алгоритма — мы должны знать входные данные заранее, что редко бывает.