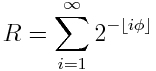Золотые строки аналогичны числам Фибоначчи, за исключением того, что используется конкатенация, а не сложение.
Начните с s 1 = «1» и s 2 = «10». Затем определите s n = s n-1 + s n-2, где «+» означает конкатенацию строк.
Первые несколько золотых струн
- «1″
- «10″
- «101″
- «10110″
- «10110101″
- …
Длина s n равна F n +1 , n + 1-е число Фибоначчи. Кроме того, s n содержит F n -1 1 и F n -2 0. (Источник: Великолепное Золотое Сечение ).
Если мы интерпретируем s n как дробную часть двоичного числа, последовательность сходится к постоянной кролика R = 0,7098034428612913…
Оказывается, что R связано с золотым сечением ф
где ⌊ i φ⌋ — наибольшее целое число, не превышающее i φ.
Вот небольшой код Python для распечатки первых нескольких золотых строк и приближение к константе кролика.
from sympy.mpmath import mp, fraction
a = "1"
b = "10"
for i in range(10):
b, a = b+a, b
print(b)
n = len(b)
mp.dps = n
denom = 2**n
num = int(b, 2)
rabbit = fraction(num, denom)
print(rabbit)
Обратите внимание, что код устанавливает количество десятичных знаков mp.dps, равное длине строки b. Это потому, что требуется ровно n знаков после запятой, чтобы точно представить рациональное число со знаменателем 2 n .