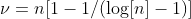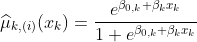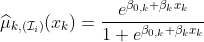Выбор переменной с использованием перекрестной проверки (и других методов)

где у нас есть наблюдения от людей, поступающих в ER, из-за (потенциального) инфаркта, и мы хотим понять, кто выжил, и построить прогностическую модель.

Что если мы используем здесь ступенчатую логистическую регрессию вперед? Я хочу использовать прямую конструкцию, поскольку она обычно уступает моделям с менее объяснительными переменными. Мы можем использовать  информационный критерий Акаике

> reg0=glm(PRONO~1,data=MYOCARDE,family=binomial)
> reg1=glm(PRONO~.,data=MYOCARDE,family=binomial)
> step(reg0,scope=formula(reg1),
+ direction="forward",k=2)                  # AIC
Start:  AIC=98.03
PRONO ~ 1

        Df Deviance    AIC
+ REPUL  1   46.884 50.884
+ INSYS  1   51.865 55.865
+ INCAR  1   53.313 57.313
+ PRDIA  1   78.503 82.503
+ PAPUL  1   82.862 86.862
+ PVENT  1   87.093 91.093
<none>       96.033 98.033
+ FRCAR  1   94.861 98.861

Step:  AIC=50.88
PRONO ~ REPUL

        Df Deviance    AIC
+ INCAR  1   44.530 50.530
+ PVENT  1   44.703 50.703
+ INSYS  1   44.857 50.857
<none>       46.884 50.884
+ PAPUL  1   45.274 51.274
+ PRDIA  1   46.322 52.322
+ FRCAR  1   46.540 52.540

Step:  AIC=50.53
PRONO ~ REPUL + INCAR

        Df Deviance    AIC
<none>       44.530 50.530
+ PVENT  1   43.134 51.134
+ PRDIA  1   43.772 51.772
+ INSYS  1   44.305 52.305
+ PAPUL  1   44.341 52.341
+ FRCAR  1   44.521 52.521

Call:  glm(formula = PRONO ~ REPUL + INCAR, family = binomial, data = MYOCARDE)

Coefficients:
(Intercept)        REPUL  
   1.633668    -0.003564  
      INCAR  
   1.618479  

Degrees of Freedom: 70 Total (i.e. Null);  68 Residual
Null Deviance:    96.03 
Residual Deviance: 44.53 AIC: 50.53

или байесовский информационный критерий Шварца ,

> step(reg0,scope=formula(reg1),
+ direction="forward",k=log(n))           # BIC
Start:  AIC=98.11
PRONO ~ 1

        Df Deviance    AIC
+ REPUL  1   46.884 51.043
+ INSYS  1   51.865 56.024
+ INCAR  1   53.313 57.472
+ PRDIA  1   78.503 82.662
+ PAPUL  1   82.862 87.021
+ PVENT  1   87.093 91.252
<none>       96.033 98.113
+ FRCAR  1   94.861 99.020

Step:  AIC=51.04
PRONO ~ REPUL

        Df Deviance    AIC
+ INCAR  1   44.530 50.768
+ PVENT  1   44.703 50.942
<none>       46.884 51.043
+ INSYS  1   44.857 51.095
+ PAPUL  1   45.274 51.512
+ PRDIA  1   46.322 52.561
+ FRCAR  1   46.540 52.778

Step:  AIC=50.77
PRONO ~ REPUL + INCAR

        Df Deviance    AIC
<none>       44.530 50.768
+ PVENT  1   43.134 51.452
+ PRDIA  1   43.772 52.089
+ INSYS  1   44.305 52.623
+ PAPUL  1   44.341 52.659
+ FRCAR  1   44.521 52.838

Call:  glm(formula = PRONO ~ REPUL + INCAR, family = binomial, data = MYOCARDE)

Coefficients:
(Intercept)        REPUL  
   1.633668    -0.003564  
      INCAR  
   1.618479  

Degrees of Freedom: 70 Total (i.e. Null);  68 Residual
Null Deviance:    96.03 
Residual Deviance: 44.53 AIC: 50.53

С этими двумя подходами, мы имеем ту же самую историю:  в наиболее важной переменной (или говорят с самой высокой прогностической ценностью) является REPUL . И мы можем улучшить модель, добавив  INCAR . Вот и все. Мы можем получить хорошую модель с этими двумя ковариатами.

Теперь, как насчет использования перекрестной проверки здесь? Мы должны помнить, что AIC асимптотически эквивалентен перекрестной проверке с одним выходом (см. Стоун (1977) ), в то время как BIC эквивалентен 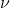перекрестной проверке с  многократной проверкой (см.  Shao (1997) ), где

Использование перекрестной проверки по принципу «один-один-выход»

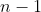
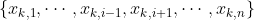
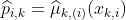
Чтобы выбрать первую переменную, рассмотрим 7 логистических регрессий, каждая на одну отдельную переменную. Каждый раз мы оцениваем модель по  наблюдениям и получаем прогноз по оставшейся,

на . Set  . Функция для получения этих значений

> name_var=names(MYOCARDE)
> pred_i=function(i,k){
+ fml = paste(name_var[8],"~",name_var[k],sep="")
+ reg=glm(fml,data=MYOCARDE[-i,],family=binomial)
+ predict(reg,newdata=MYOCARDE[i,],
+ type="response")
+ }

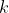
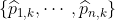
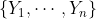
то для каждой переменной  , мы получим ROC кривую , используя  и ,

> library(AUC)
> ROC=function(k){
+  Y=MYOCARDE[,8]=="Survival"
+  S=Vectorize(function(i) pred_i(i,k))
+ (1:length(Y))
+  R=roc(S,as.factor(Y))
+  return(list(roc=cbind(R$fpr,R$tpr),
+              auc=AUC::auc(R)))
+ }

Здесь для каждой переменной мы вычисляем площадь под кривой ( критерий AUC )

> AUC=rep(NA,7)
> for(k in 1:7){
+   AUC[k]=ROC(k)$auc
+   cat("Variable ",k,"(",name_var[k],") :",
+   AUC[k],"\n") }
Variable  1 ( FRCAR ) : 0.4934319 
Variable  2 ( INCAR ) : 0.8965517 
Variable  3 ( INSYS ) : 0.909688 
Variable  4 ( PRDIA ) : 0.7487685 
Variable  5 ( PAPUL ) : 0.7134647 
Variable  6 ( PVENT ) : 0.6584565 
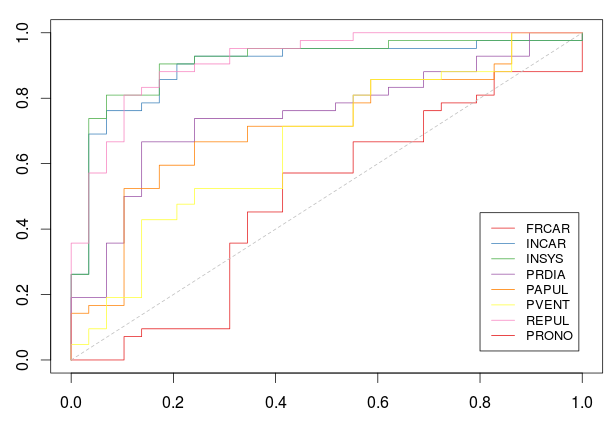
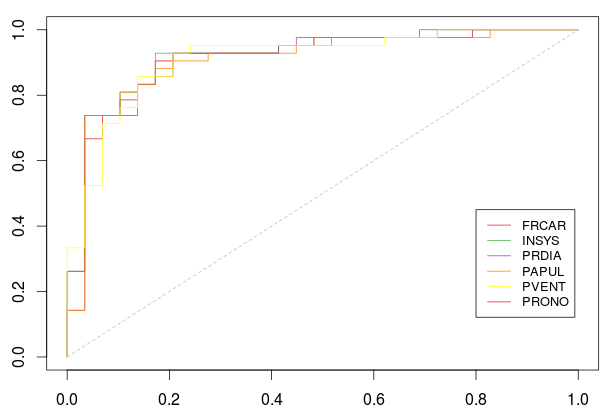
Variable  7 ( REPUL ) : 0.9154351

Но мы также можем визуализировать эти кривые,

> plot(0:1,0:1,col="white",xlab="",ylab="")
> for(k in 1:7) 
+ lines(ROC(k)$roc,type="s",col=CL[k])
> legend(.8,.45,name_var,col=CL,lty=1,cex=.8)

(здесь нет PRONO, в Легенде есть опечатка)

где здесь цвета были получены с использованием

> library(RColorBrewer)
> CL=brewer.pal(8, "Set1")[-7]

Здесь кривые ROC были получены с использованием стратегии Leave-one-Out. И лучшая переменная (если мы должны оставить один и только один)

> k0=which.max(AUC)
> name_var[k0]
[1] "REPUL"

Теперь рассмотрим пошаговую процедуру: мы сохраняем эту «лучшую» переменную в нашей модели и пытаемся добавить еще одну.

> pred_i=function(i,k){
+ vk=c(k0,k)
+ fml = paste(name_var[8],"~",paste(name_var[vk],
+ collapse="+"),sep="")
+ reg=glm(fml,data=MYOCARDE[-i,],family=binomial)
+ predict(reg,newdata=MYOCARDE[i,],
+ type="response")
+ }
> library(AUC)
> ROC=function(k){
+ Y=MYOCARDE[,8]=="Survival"
+ S=Vectorize(function(i) pred_i(i,k))
+ (1:length(Y))
+ R=roc(S,as.factor(Y))
+ return(list(roc=cbind(R$fpr,R$tpr),
+ auc=AUC::auc(R)))
+ }
> plot(0:1,0:1,col="white",xlab="",ylab="")
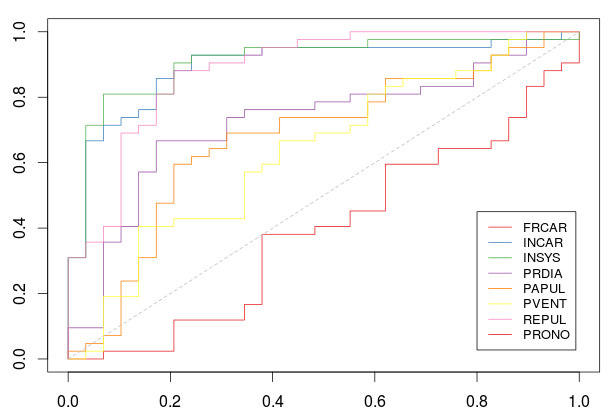
> for(k in (1:7)[-k0]) lines(ROC(k)$roc,type="s",col=CL[k])
> segments(0,0,1,1,lty=2,col="grey")
> legend(.8,.45,
+   name_var[-k0],
+   col=CL[-k0],lty=1,cex=.8)

Мы были уже довольно хорошо. И мы могли бы ожидать найти другую переменную, которая увеличит предсказательную силу нашего классификатора.

> AUC=rep(NA,7)
> for(k in (1:7)[-k0]){
+  AUC[k]=ROC(k)$auc
+  cat("Variable ",k,"(",name_var[k],") :",
+  AUC[k],"\n")
+ }
Variable  1 ( FRCAR ) : 0.9064039 
Variable  2 ( INCAR ) : 0.9195402 
Variable  3 ( INSYS ) : 0.9187192 
Variable  4 ( PRDIA ) : 0.9137931 
Variable  5 ( PAPUL ) : 0.9187192 
Variable  6 ( PVENT ) : 0.9137931

И, конечно, мы можем двигаться вперед, добавить еще одну переменную и т. Д.,

> k0=c(k0,which.max(AUC))

> pred_i=function(i,k){
+   vk=c(k0,k)
+   fml = paste(name_var[8],"~",paste(
+ name_var[vk],collapse="+"),sep="")
+ reg=glm(fml,data=MYOCARDE[-i,],family=binomial)
+ predict(reg,newdata=MYOCARDE[i,],
+ type="response")
+ }
> library(AUC)
> ROC=function(k){
+  Y=MYOCARDE[,8]=="Survival"
+  S=Vectorize(function(i) pred_i(i,k))
+  (1:length(Y))
+  R=roc(S,as.factor(Y))
+  return(list(roc=cbind(R$fpr,R$tpr),
+  auc=AUC::auc(R)))
+ }
> 
> plot(0:1,0:1,col="white",xlab="",ylab="")
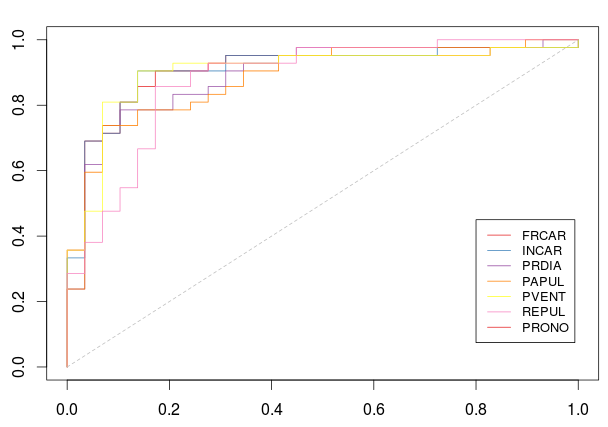
> for(k in (1:7)[-k0]) lines(ROC(k)$roc,type="s",col=CL[k])
> segments(0,0,1,1,lty=2,col="grey")
> legend(.8,.45,name_var[-k0],
+ col=CL[-k0],lty=1,cex=.8)

Но здесь выигрыш довольно небольшой (если есть)

> AUC=rep(NA,7)
> for(k in (1:7)[-k0]){
+ AUC[k]=ROC(k)$auc
+ cat("Variable ",k,"(",name_var[k],") :",
+ AUC[k],"\n")
+ }
Variable  1 ( FRCAR ) : 0.9121511 
Variable  3 ( INSYS ) : 0.9170772 
Variable  4 ( PRDIA ) : 0.910509 
Variable  5 ( PAPUL ) : 0.907225 
Variable  6 ( PVENT ) : 0.909688

С этим пошаговым алгоритмом лучшая стратегия состоит в том, чтобы сначала сохранить  REPUL , а затем добавить  INCAR . Что согласуется с пошаговой процедурой с использованием информационного критерия Акаике.

Альтернативой может быть выбор лучшей пары среди всех возможных пар. Это займет много времени, но его можно использовать, чтобы избежать пошагового недостатка.

> pred_i=function(i,k){
+ fml = paste(name_var[8],"~",paste(name_var[
+ as.integer(k)],collapse="+"),sep="")
+ reg=glm(fml,data=MYOCARDE[-i,],family=binomial)
+ predict(reg,newdata=MYOCARDE[i,],
+ type="response")
+ }
> library(AUC)
> ROC=function(k){
+   Y=MYOCARDE[,8]=="Survival"
+   L=list()
+   n=length(Y)
+   nk=trunc(n/trunc(n/10))
+   for(i in 1:(nk-1)) L[[i]]=((i-1)*
+     trunc(n/10)+1:(n/10)) 
+   L[[nk]]=((nk-1)*trunc(n/10)+1):n
+   S=unlist(Vectorize(function(i) 
+     pred_i(L[[i]],k))(1:nk))
+   R=roc(S,as.factor(Y))
+   return(AUC::auc(R))
+ }

> v=data.frame(k1=rep(1:7,each=7),k2=rep(1:7,7))
> v=v[v$k1<v$k2,]
> v$auc=NA
> for(i in 1:nrow(v)) v$auc[i]=ROC(v[i,1:2])
> v
   k1 k2       auc
2   1  2 0.9047619
3   1  3 0.9047619
4   1  4 0.6990969
5   1  5 0.6395731
6   1  6 0.6334154
7   1  7 0.8817734
10  2  3 0.9072250
11  2  4 0.9088670
12  2  5 0.8940887
13  2  6 0.8801314
14  2  7 0.8899836
18  3  4 0.8916256
19  3  5 0.8817734
20  3  6 0.9014778
21  3  7 0.8768473
26  4  5 0.6925287
27  4  6 0.7138752
28  4  7 0.8825944
34  5  6 0.6912972
35  5  7 0.8834154
42  6  7 0.8834154

Здесь лучшая пара

> v[which.max(v$auc),]
   k1 k2      auc
11  2  4 0.908867
> name_var[as.integer(v[which.max(v$auc),1:2])]
[1] "INCAR" "PRDIA"

which is different, compared with the one we got above. What is odd here is that we get a smaller AUC than the ones we got at step 2 in the stepwise procedure.

Nevertheless, even with a few observations (our dataset is rather small here), it is time consuming to look at all ROC curves, for all pairs. An alternative might be to use –Fold Cross Validation.

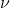Using -Fold Cross Validation

Here we consider a partition of indices, 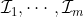, and we define

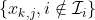
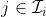
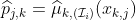
based on observations. For all, set . Then, we can use the stepwise method described above

> pred_i=function(i,k){
+ fml = paste(name_var[8],"~",name_var[k],sep="")
+ reg=glm(fml,data=MYOCARDE[-i,],family=binomial)
+ predict(reg,newdata=MYOCARDE[i,],
+ type="response")
+ }
> library(AUC)
> ROC=function(k){
+   Y=MYOCARDE[,8]=="Survival"
+   L=list()
+   n=length(Y)
+   nk=trunc(n/trunc(n/10))
+   for(i in 1:(nk-1)) L[[i]]=((i-1)*
+     trunc(n/10)+1:(n/10)) 
+   L[[nk]]=((nk-1)*trunc(n/10)+1):n
+   S=unlist(Vectorize(function(i) 
+     pred_i(L[[i]],k))(1:nk))
+   R=roc(S,as.factor(Y))
+   return(list(roc=cbind(R$fpr,R$tpr),
+               auc=AUC::auc(R)))
+ }

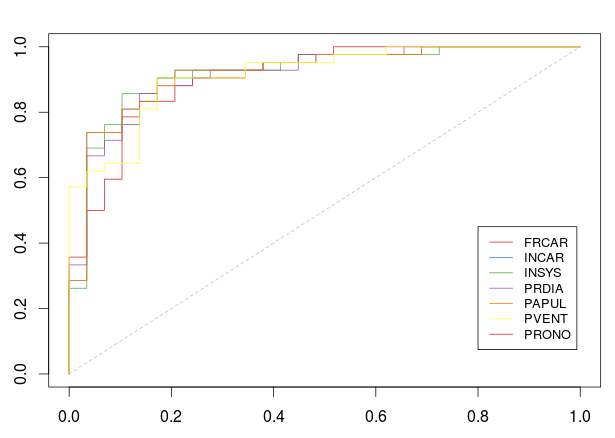
> plot(0:1,0:1,col="white",xlab="",ylab="")
> for(k in (1:7)) lines(ROC(k)$roc,col=CL[k])
> segments(0,0,1,1,lty=2,col="grey")
> legend(.8,.45,name_var,col=CL,lty=1,cex=.8)

with

> AUC=rep(NA,7)
> for(k in 1:7){
+ AUC[k]=ROC(k)$auc
+ cat("Variable ",k,"(",name_var[k],") :",
+ AUC[k],"\n")
+ }
Variable  1 ( FRCAR ) : 0.3932677 
Variable  2 ( INCAR ) : 0.8940887 
Variable  3 ( INSYS ) : 0.908046 
Variable  4 ( PRDIA ) : 0.7278325 
Variable  5 ( PAPUL ) : 0.6756979 
Variable  6 ( PVENT ) : 0.63711 
Variable  7 ( REPUL ) : 0.8834154

So, this time, INSYS is probably the best covariate to use. Now, if we keep that variable, and move forward,

> k0=which.max(AUC)

> pred_i=function(i,k){
+  vk=c(k0,k)
+ fml = paste(name_var[8],"~",paste(name_var[vk],
+ collapse="+"),sep="")
+ reg=glm(fml,data=MYOCARDE[-i,],family=binomial)
+ predict(reg,newdata=MYOCARDE[i,],
+ type="response")
+ }
> library(AUC)
> ROC=function(k){
+   Y=MYOCARDE[,8]=="Survival"
+   L=list()
+   n=length(Y)
+   nk=trunc(n/trunc(n/10))
+   for(i in 1:(nk-1)) L[[i]]=((i-1)*
+     trunc(n/10)+1:(n/10)) 
+   L[[nk]]=((nk-1)*trunc(n/10)+1):n
+   S=unlist(Vectorize(function(i) 
+      pred_i(L[[i]],k))(1:nk))
+   R=roc(S,as.factor(Y))
+   return(list(roc=cbind(R$fpr,R$tpr),
+               auc=AUC::auc(R)))
+ }

> plot(0:1,0:1,col="white",xlab="",ylab="")
> for(k in (1:7)[-k0]) 
+ lines(ROC(k)$roc,col=CL[k])
> segments(0,0,1,1,lty=2,col="grey")
> legend(.8,.45,name_var[-k0],
+        col=CL[-k0],lty=1,cex=.8)

and our best choice for the second variable would be INCAR

> AUC=rep(NA,7)
> for(k in (1:7)[-k0]){
+   AUC[k]=ROC(k)$auc
+   cat("Variable ",k,"(",name_var[k],") :",
+ AUC[k],"\n")
+ }
Variable  1 ( FRCAR ) : 0.9047619 
Variable  2 ( INCAR ) : 0.907225 
Variable  4 ( PRDIA ) : 0.8916256 
Variable  5 ( PAPUL ) : 0.8817734 
Variable  6 ( PVENT ) : 0.9014778 
Variable  7 ( REPUL ) : 0.8768473 
> which.max(AUC)
[1] 2

Here again, it is possible to look at all pairs

> pred_i=function(i,k){
+ fml = paste(name_var[8],"~",paste(name_var[
+ as.integer(k)],collapse="+"),sep="")
+ reg=glm(fml,data=MYOCARDE[-i,],family=binomial)
+ predict(reg,newdata=MYOCARDE[i,],
+ type="response")
+ }
> library(AUC)
> ROC=function(k){
+   Y=MYOCARDE[,8]=="Survival"
+   L=list()
+   n=length(Y)
+   nk=trunc(n/trunc(n/10))
+   for(i in 1:(nk-1)) L[[i]]=((i-1)*
+   trunc(n/10)+1:(n/10)) 
+   L[[nk]]=((nk-1)*trunc(n/10)+1):n
+   S=unlist(Vectorize(function(i) 
+     pred_i(L[[i]],k))(1:nk))
+   R=roc(S,as.factor(Y))
+   return(AUC::auc(R))
+ }

> v=data.frame(k1=rep(1:7,each=7),k2=rep(1:7,7))
> v=v[v$k1<v$k2,]
> v$auc=NA
> for(i in 1:nrow(v)) v$auc[i]=ROC(v[i,1:2])
> v[which.max(v$auc),]
   k1 k2      auc
11  2  4 0.908867
> name_var[as.integer(v[which.max(v$auc),1:2])]
[1] "INCAR" "PRDIA"

which is the same as what we got using an One-Leave-Out strategy: we have again the same two covariates. And again, the AUC is lower than the one we got using a stepwise procedure (I still don’t understand how this is possible).   An alternative for the code would be to store all the regression models in a list,

> L=list()
> n=nrow(MYOCARDE)
> nk=trunc(n/trunc(n/10))
> for(i in 1:(nk-1)) L[[i]]=((i-1)*trunc(n/10)+
+  1:(n/10)) 
> L[[nk]]=((nk-1)*trunc(n/10)+1):n
> REG=list()
> for(k in 1:7){
+   REG[[k]]=list()
+   fml = paste(name_var[8],"~",
+ paste(name_var[as.integer(k)],collapse="+"),
+ sep="")
+ for(i in 1:nk) REG[[k]][[i]]=reg=glm(fml,
+  data=MYOCARDE[-L[[i]],],family=binomial)
+ }

and then to call them, properly

> pred_i=function(i,k){
+  I=which(sapply(1:10,function(j) i%in%L[[j]]))
+  predict(REG[[k]][[I]],newdata=MYOCARDE[i,],
+  type="response")
+ }

One has to check about the efficiency, especially with a large dataset.

Using Trees and Random Forests

Another quick, but popular (from what I’ve seen), technique is to use trees. Important variables should appear in the output,

> library(rpart)
> tree=rpart(PRONO~.,data=MYOCARDE)
> library(rpart.plot)
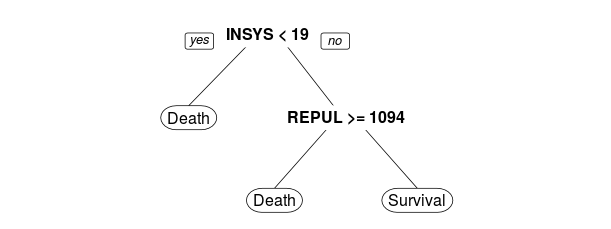
> rpart.plot(tree)

Here, the first variable that appears in the tree construction is INSYS, and the second on is REPUL. Which is rather different with what we got above. But using one tree is maybe not sufficient. One can use the variable importance function (described in a previous post) obtained using random forests.

> library(randomForest)
> rf=randomForest(PRONO~.,data=MYOCARDE,
+                 importance=TRUE)
> rf$importance[,4]
   FRCAR    INCAR    INSYS 
1.042006 7.363255 8.954898 
   PRDIA    PAPUL    PVENT 
3.149235 2.571267 3.152619 
   REPUL 
7.510110

Here, we have the same story as the one we got with a simple tree: the ‘most important’ variable is INSYS while the second one is REPUL. But here, we consider tree based predictors. And not a logistic regression.

Using Dedicated R functions

It is possible to use some dedicated R functions for variable selection. For instance, since we consider a logistic regression, use

> library(bestglm)
> Xy=as.data.frame(MYOCARDE)
> Xy[,8]=(Xy[,8]=="Death")*1             
> names(Xy)=names(MYOCARDE)
> B=bestglm(Xy)
> B$Subsets[,2:8]
   FRCAR INCAR INSYS PRDIA PAPUL PVENT REPUL
0  FALSE FALSE FALSE FALSE FALSE FALSE FALSE
1  FALSE FALSE FALSE FALSE FALSE FALSE  TRUE
2* FALSE  TRUE FALSE FALSE FALSE FALSE  TRUE
3  FALSE  TRUE FALSE FALSE FALSE  TRUE  TRUE
4   TRUE  TRUE FALSE FALSE FALSE  TRUE  TRUE
5   TRUE  TRUE  TRUE FALSE FALSE  TRUE  TRUE
6   TRUE  TRUE FALSE  TRUE  TRUE  TRUE  TRUE
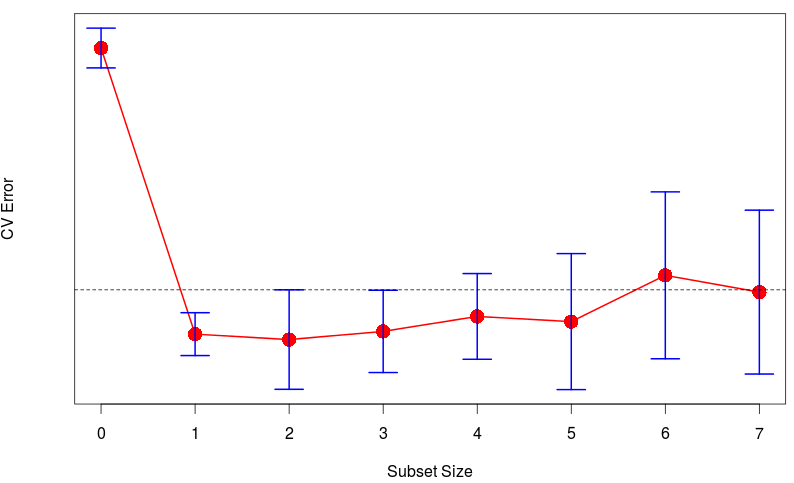
7   TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE

With only one variable, we should consider REPUL (row 1 of the matrix), while with two variables, we should consider REPUL and INCAR (and that is the best model, based on some Bayesian Information Criterion). Here, cross validation techniques can be used also,

> B=bestglm(Xy, IC = "CV", CVArgs = 
+ list(Method = "HTF", K = 10, REP = 1))
>  cverrs = B$Subsets[, "CV"]
>  sdCV = B$Subsets[, "sdCV"]
>  CVLo = cverrs - sdCV
>  CVHi = cverrs + sdCV
>  ymax = max(CVHi)
>  ymin = min(CVLo)
>  k = 0:(length(cverrs) - 1)
>  plot(k, cverrs, ylim = c(ymin,
+  ymax), type = "n", yaxt = "n")
>  points(k,cverrs,cex = 2,col="red",pch=16)
>  lines(k, cverrs, col = "red", lwd = 2)
>  axis(2, yaxp = c(0.6, 1.8, 6))
>  segments(k, CVLo, k, CVHi,col="blue", lwd = 2)
>  eps = 0.15
>  segments(k-eps, CVLo, k+eps, CVLo, 
+ col = "blue", lwd = 2)
>  segments(k-eps, CVHi, k+eps, CVHi, 
+ col = "blue", lwd = 2)
>  indMin = which.min(cverrs)
>  fmin = sdCV[indMin]
>  cutOff = fmin + cverrs[indMin]
>  abline(h = cutOff, lty = 2)
>  indMin = which.min(cverrs)
>  fmin = sdCV[indMin]
>  cutOff = fmin + cverrs[indMin]
>  min(which(cverrs < cutOff))
[1] 2

If we summarize, here,

• stepwise, AIC : REPUL + INCAR
• stepwise, BIC : REPUL + INCAR
• One-leave-Out CV stepwise : REPUL + INCAR
• One-leave-Out CV pairs : INCAR + PRDIA
• -fold CV stepwise : INSYS + INCAR
• -fold CV pairs : INCAR + PRDIA
• Tree : INSYS + REPUL
• Variable Importance (RF) : INSYS + INCAR
• Best GLM : REPUL + INCAR

That is the lovely part with statistical tools: there are usually multiple (valid) answers. And this is why machine learning is difficult: if there was a single answer, any machine could built up a model that works well. But obviously, it has to be more complicated…