Чтобы проиллюстрировать проблему выбора модели классификации, рассмотрим некоторые моделируемые данные,
> n = 500
> set.seed(1)
> X = rnorm(n)
> ma = 10-(X+1.5)^2*2
> mb = -10+(X-1.5)^2*2
> M = cbind(ma,mb)
> set.seed(1)
> Z = sample(1:2,size=n,replace=TRUE)
> Y = ma*(Z==1)+mb*(Z==2)+rnorm(n)*5
> df = data.frame(Z=as.factor(Z),X,Y)Первая стратегия состоит в том, чтобы разбить набор данных на две части: набор обучающих данных и набор тестируемых данных.
> df1 = training = df[1:300,]
> df2 = testing = df[301:500,]Метод удержания: наборы данных для обучения и тестирования
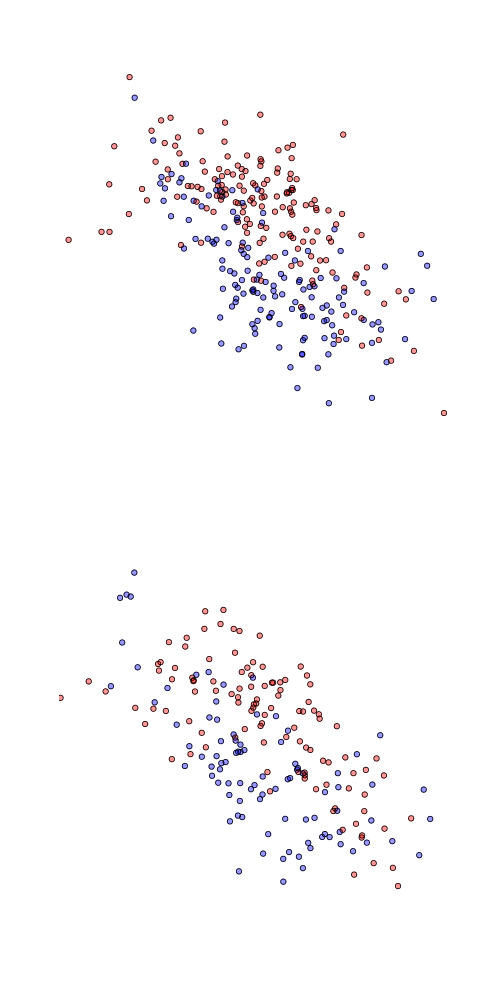
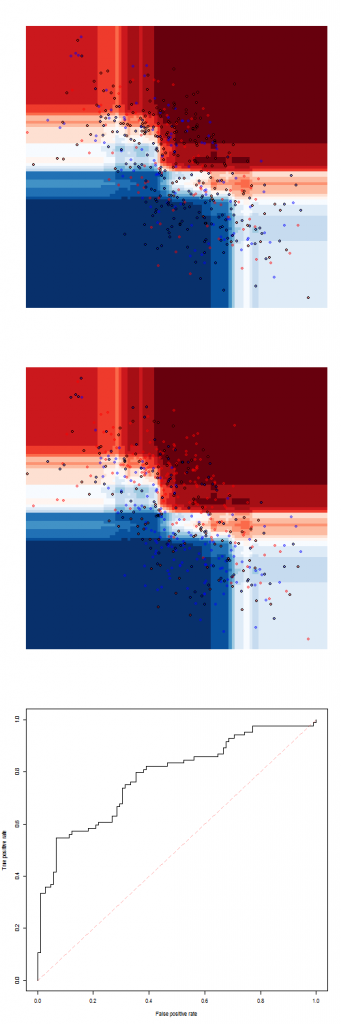
Два набора данных могут быть отображены ниже, с обучающим набором данных сверху и тестовым набором данных ниже
> plot(df1$X,df1$Y,pch=19,col=c(rgb(1,0,0,.4),
+ rgb(0,0,1,.4))[df1$Z])Мы можем рассмотреть простое дерево классификации.
> library(rpart)
> fit = rpart(Z~X+Y,data=df1)
> pred = function(x,y) predict(fit,newdata=data.frame(X=x,Y=y))[,1]
Чтобы визуализировать это, используйте
> vx=seq(-3,3,length=101)
> vy=seq(-25,25,length=101)
> z=matrix(NA,length(vx),length(vy))
> for(i in 1:length(vx)){
+ for(j in 1:length(vy))
+ {z[i,j]=pred(vx[i],vy[j])}}и
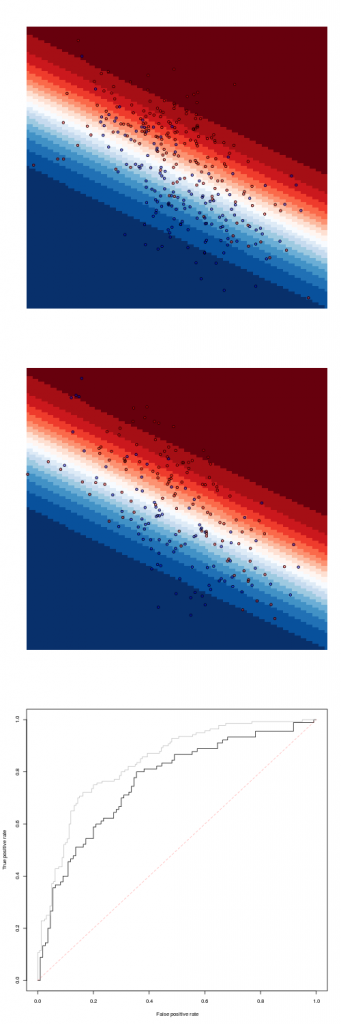
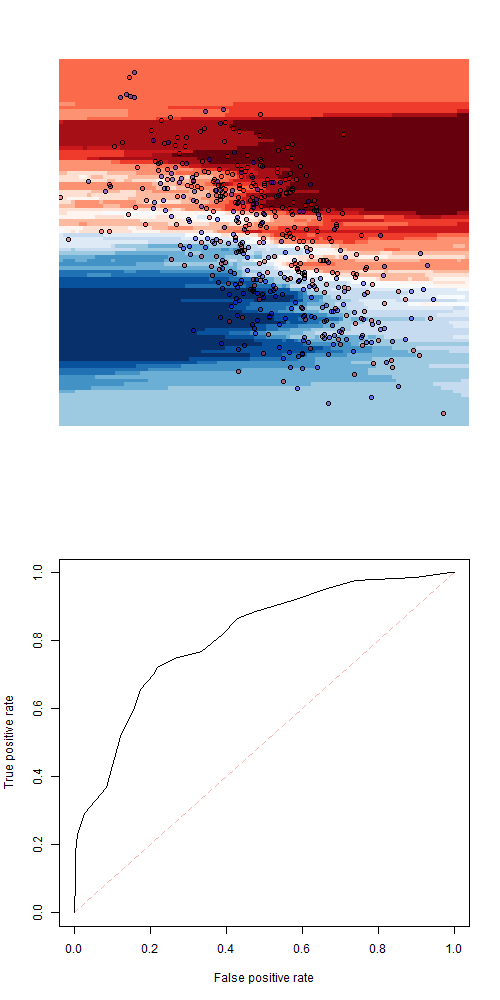
> image(vx,vy,z,axes=FALSE,xlab="",ylab="")
> points(df1$X,df1$Y,pch=19,col=c(rgb(1,0,0,.4),
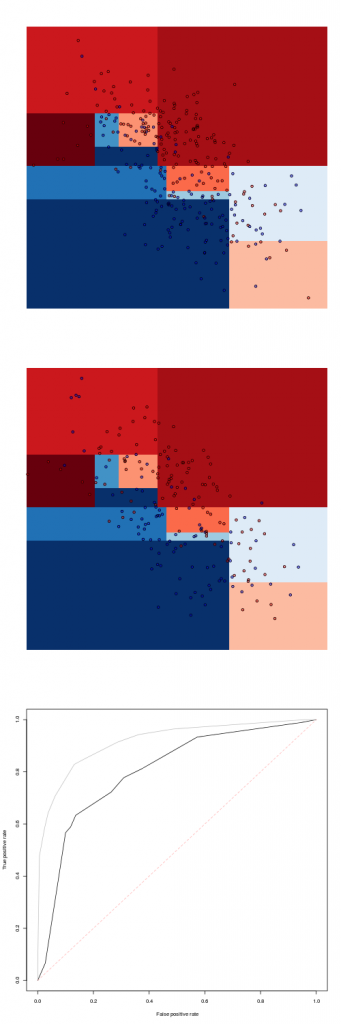
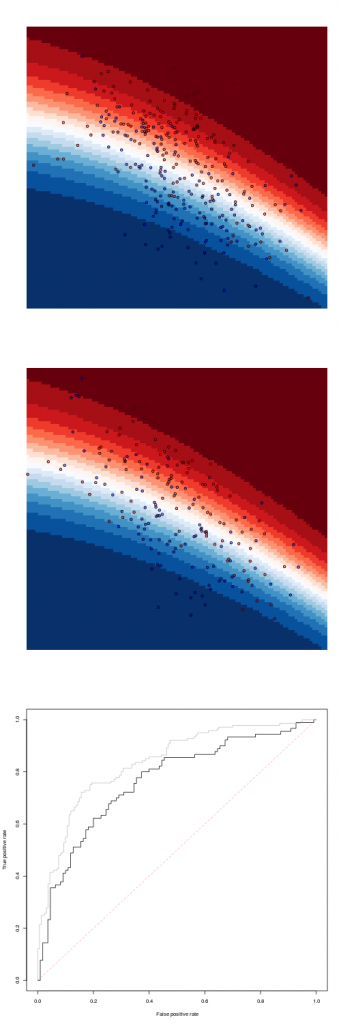
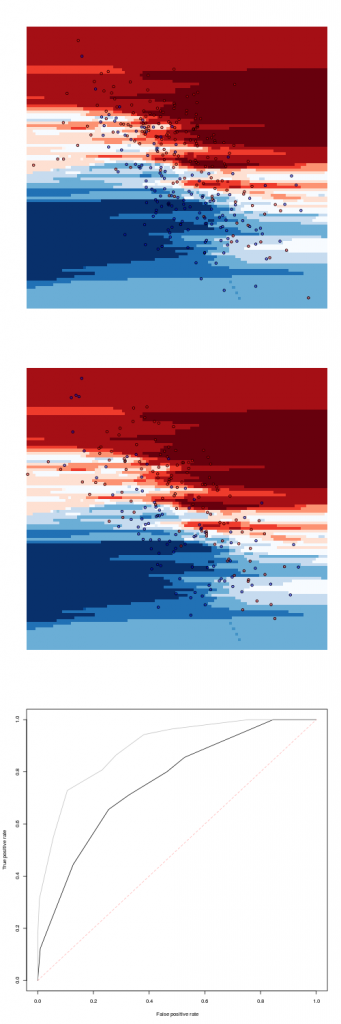
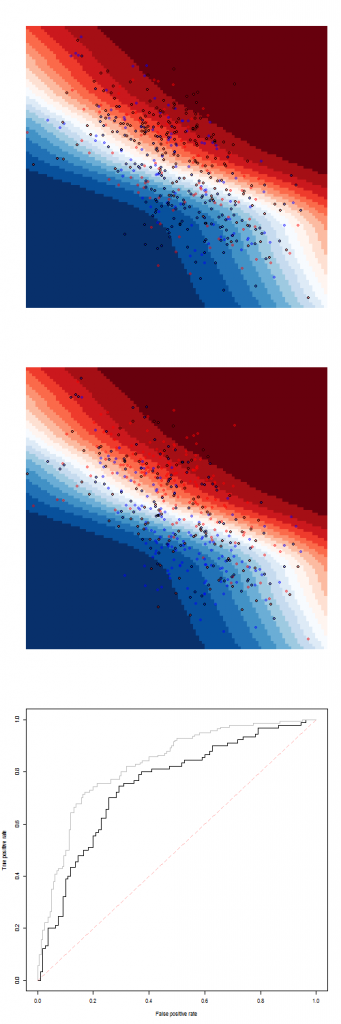
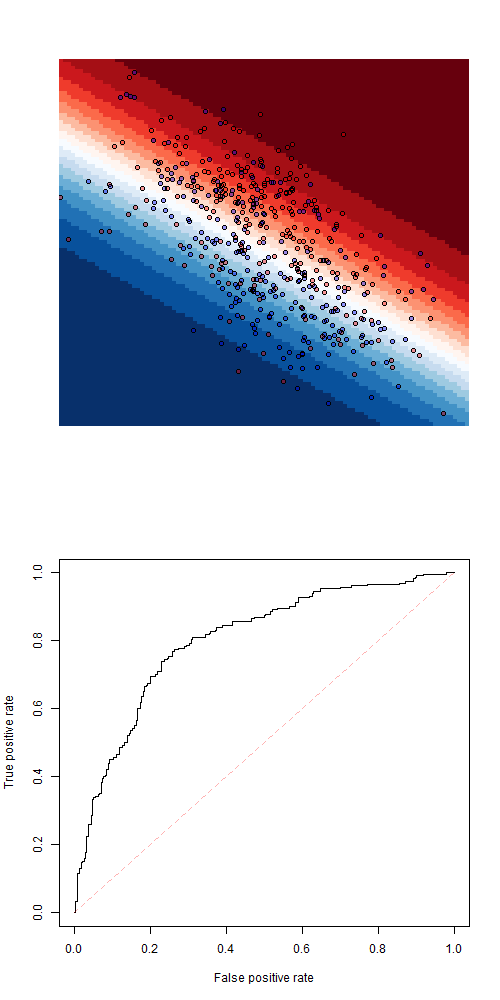
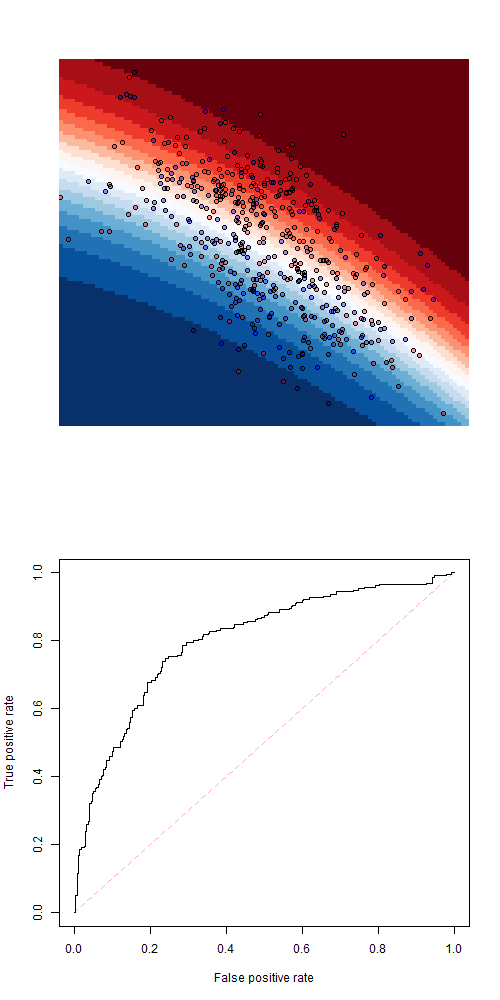
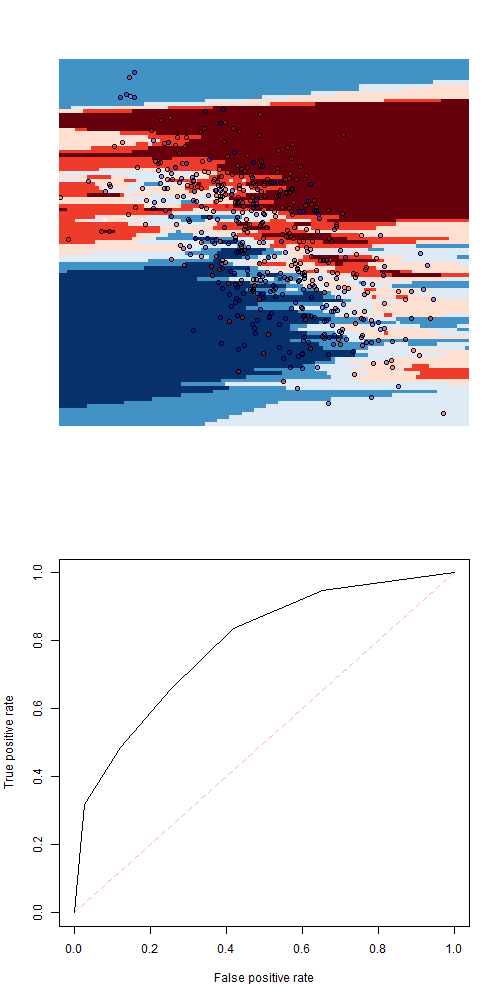
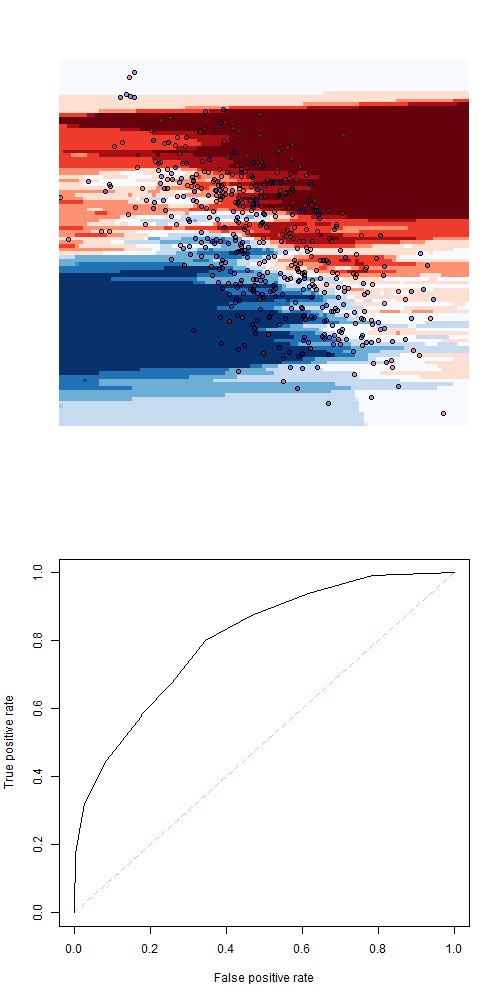
+ rgb(0,0,1,.4))[df1$Z])Мы имеем сверху прогноз на наборе обучающих данных, затем ниже прогноз на наборе тестовых данных. И, наконец, внизу кривая ROC для тестового набора данных (черная кривая), а также тренировочный набор данных (серая кривая)
> Y1=as.numeric(df1$Z)-1
> Y2=as.numeric(df2$Z)-1
> library(ROCR)
> S1 = predict(fit,newdata=df1)[,1]
> S2 = predict(fit,newdata=df2)[,1]
> pred <- prediction( S2, Y2 )
> perf <- performance( pred, "tpr", "fpr" )
> plot( perf )
> pred <- prediction( S1, Y1 )
> perf <- performance( pred, "tpr", "fpr" )
> plot( perf ,add=TRUE,col="grey")Исходя из этого дерева, естественно получить прогноз, используя случайный лес
> library(randomForest)
> fit=randomForest(Z~X+Y,data=df1)
Чтобы получить прогноз, используйте
> pred=function(x,y)
+ predict(fit,newdata=data.frame(X=x,Y=y),
+ type="prob")[,2]Не то, чтобы подгонка идеально подходила к тренировочному образцу. Другой популярной моделью может быть логистическая регрессия.
> fit=glm(Z~X+Y,data=df1,family=binomial)
> pred=function(x,y)
+ predict(fit,newdata=data.frame(X=x,Y=y),
+ type="response")Последнее очень близко к линейному дискриминантному анализу
> library(MASS)
> fit=lda(Z~X+Y,data=df1,family=binomial)
> pred=function(x,y)
+ predict(fit,newdata=
+ data.frame(X=x,Y=y))$posterior[,2]или квадратичный дискриминантный анализ
> fit=qda(Z~X+Y,data=df1,family=binomial)
> pred=function(x,y)
+ predict(fit,newdata=
+ data.frame(X=x,Y=y))$posterior[,2]Чтобы попробовать самые разные модели, рассмотрим k- ближайшего соседа
(здесь с 9 соседями)
> library(caret)
> fit=knn3(Z~X+Y,data=df1,k=9)
> pred=function(x,y)
+ predict(fit,newdata=data.frame(X=x,Y=y))[,2]некоторая логистическая регрессия с двумерными сплайнами
> library(mgcv)
> fit=gam(Z~s(X,Y),data=df1,family=binomial)
> pred=function(x,y)
+ predict(fit,newdata=data.frame(X=x,Y=y),
+ type="response")или какой-то алгоритм повышения градиента
> library(dismo)
> df1$Z01 = 1*(df1$Z=="2")
> fit=gbm.step(data=df1, gbm.x = 2:3, gbm.y = 4,
+ family = "bernoulli", tree.complexity = 5,
+ learning.rate = 0.01, bag.fraction = 0.5)
> pred = function(x,y)
+ predict(fit,newdata=data.frame(X=x,Y=y),
+ type="response",n.trees=400)Тем не менее, использование этого метода для создания некоторых обучающих и тестовых наборов данных может быть затруднено. Это можно сделать только тогда, когда у нас много наблюдений. И даже в этом случае мы все еще можем быть неудачниками при создании тестового образца (просто из-за неудачи). Альтернативой является использование перекрестной проверки.
Использование перекрестной проверки
Здесь мы рассматриваем перекрестную проверку с одним пропуском (но можно также рассмотреть перекрестную проверку с v- кратным увеличением, чтобы получить результаты быстрее).
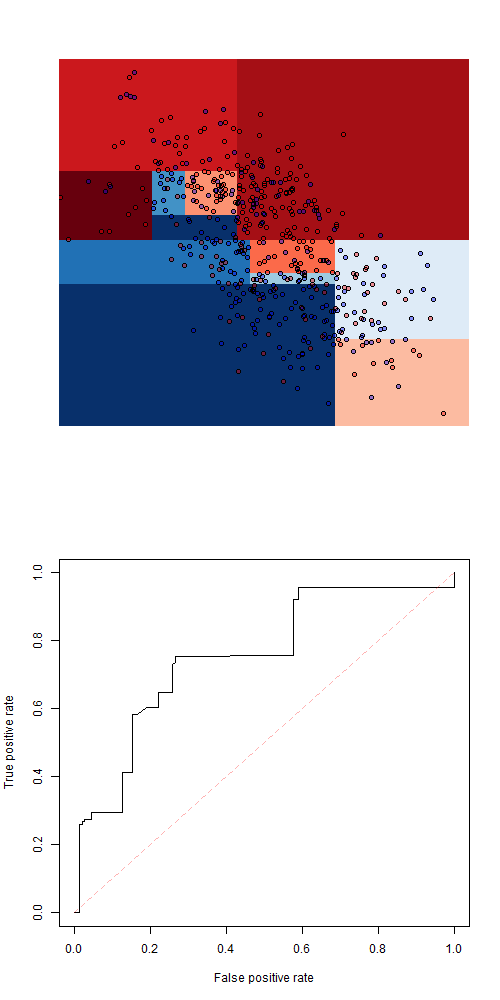
Рассмотрим здесь дерево классификации . Например, для получения кривой ROC перекрестной проверки используйте
> FIT=list()
> for(i in 1:n)
+ FIT[[i]] = rpart(Z~X+Y,data=df[-i,])
> predict_i = function(i)
+ predict(FIT[[i]],newdata=df[i,])[,2]
> S = Vectorize(predict_i)(1:n)Здесь я храню n моделей, где каждый раз удаляется одно наблюдение, а затем я получаю прогноз для удаленного наблюдения. И мы можем сгенерировать ROC-кривую
> Y = as.numeric(df$Z)-1
> library(ROCR)
> pred = prediction( S, Y )
> perf = performance( pred, "tpr", "fpr" )
> plot( perf )Конечно, можно легко получить код, который работает быстрее, но он работает с этим небольшим набором данных.
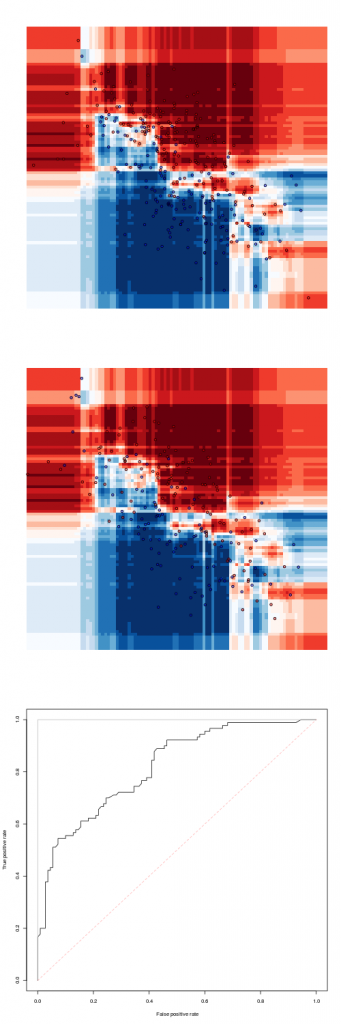
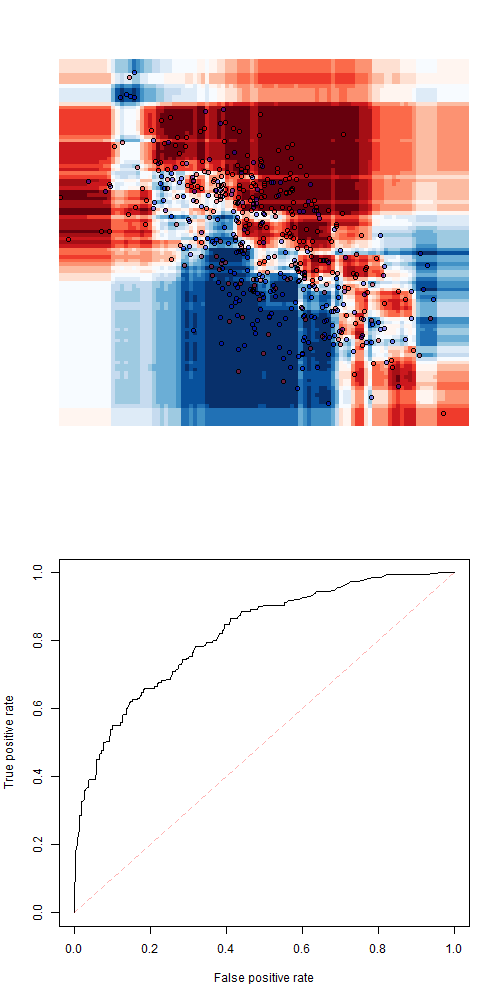
Если мы рассмотрим случайный лес , мы получим
> FIT=list()
> for(i in 1:n)
+ FIT[[i]] = randomForest(Z~X+Y,data=df[-i,])
> predict_i = function(i)
+ predict(FIT[[i]],newdata=df[i,],
+ type="prob")[,2]
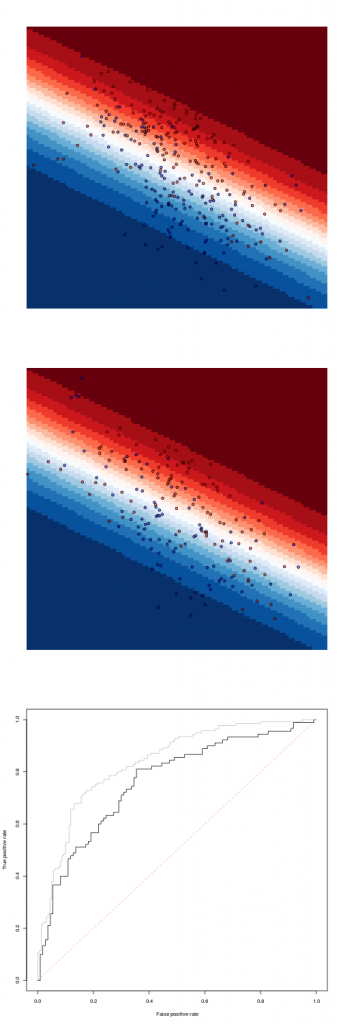
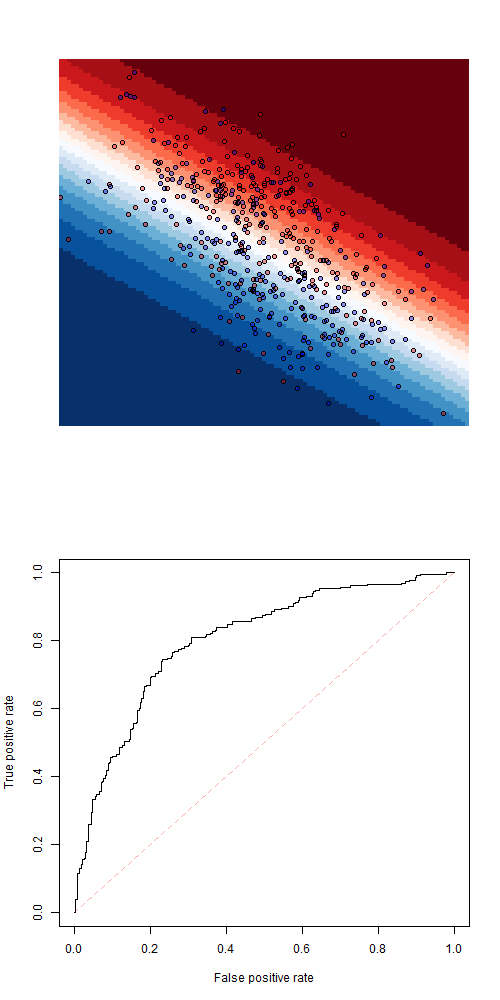
> S = Vectorize(predict_i)(1:n)Можно рассмотреть логистическую регрессию
> FIT=list()
> for(i in 1:n)
+ FIT[[i]] = glm(Z~X+Y,data=df[-i,],
+ family=binomial)
> predict_i = function(i)
+ predict(FIT[[i]],newdata=df[i,],
+ type="response")
> S = Vectorize(predict_i)(1:n)или линейный дискриминантный анализ
> FIT=list()
> for(i in 1:n)
+ FIT[[i]] = lda(Z~X+Y,data=df[-i,],
+ family=binomial)
> predict_i = function(i)
+ predict(FIT[[i]],newdata=df[i,])$posterior[,2]
> S = Vectorize(predict_i)(1:n)в то время как квадратичный дискриминантный анализ дает
> FIT=list()
> for(i in 1:n)
+ FIT[[i]] = qda(Z~X+Y,data=df[-i,],
+ family=binomial)
> predict_i = function(i)
+ predict(FIT[[i]],newdata=df[i,])$posterior[,2]
> S = Vectorize(predict_i)(1:n)Опять же, если мы рассмотрим другой тип модели, такой как k- ближайший сосед (с k = 5), мы получим
> FIT=list()
> for(i in 1:n)
+ FIT[[i]] = knn3(Z~X+Y,data=df[-i,],k=5)
> predict_i = function(i)
+ predict(FIT[[i]],newdata=df[i,])[,2]
> S = Vectorize(predict_i)(1:n)или k ближайшего соседа с k = 9
или к = 21
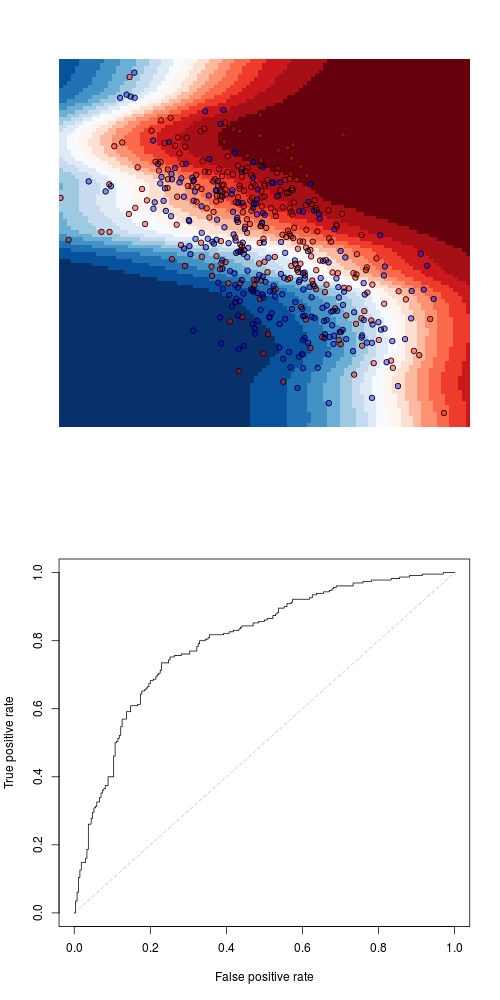
Можно также рассмотреть логистическую регрессию с двумерными сплайнами
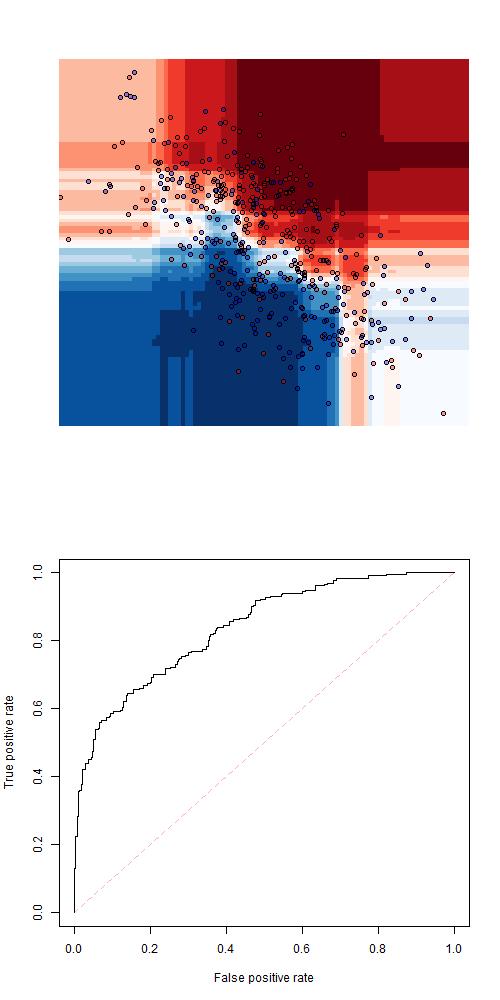
или, что не менее важно, некоторая модель повышения градиента . На этом у нас могут возникнуть проблемы с сохранением 500 выходных данных от функции повышения градиента (выходной сигнал большой). Более быстрый код может быть
> VS = rep(NA,n)
> for(i in 1:n){
+ FIT = gbm.step(data=df[-i,],
+ gbm.x = 2:3, gbm.y = 4, family = "bernoulli",
+ tree.complexity = 5, learning.rate = 0.01,
+ bag.fraction = 0.5)
+ VS[i] = predict(FIT,newdata=df[i,],
+ n.trees=400)
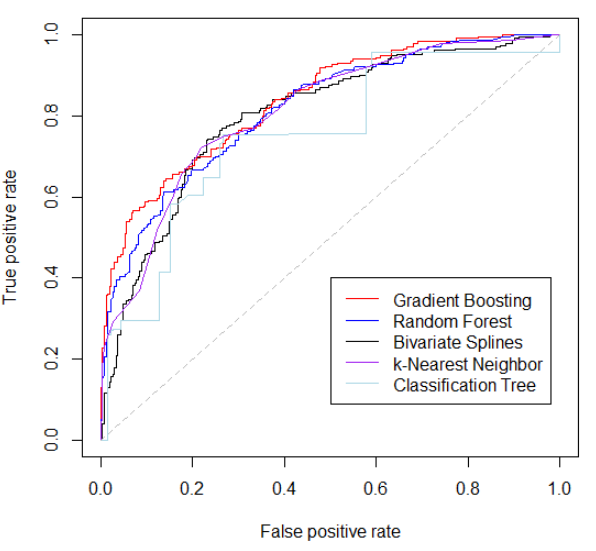
+ }Фактически, теперь можно сравнить все эти модели со всеми кривыми ROC на одном графике: