Я говорил с кем-то на днях о визуализации, которую я вспомнил, увидев несколько лет назад, которая могла бы помочь установить разумное значение для порогового значения для метрики. Как я уже писал , пороговые значения — это в основном неправильный способ мониторинга систем, но если вы собираетесь их использовать, я думаю, что есть простые вещи, которые вы можете сделать, чтобы избежать того, чтобы пороговые значения были совершенно произвольными.
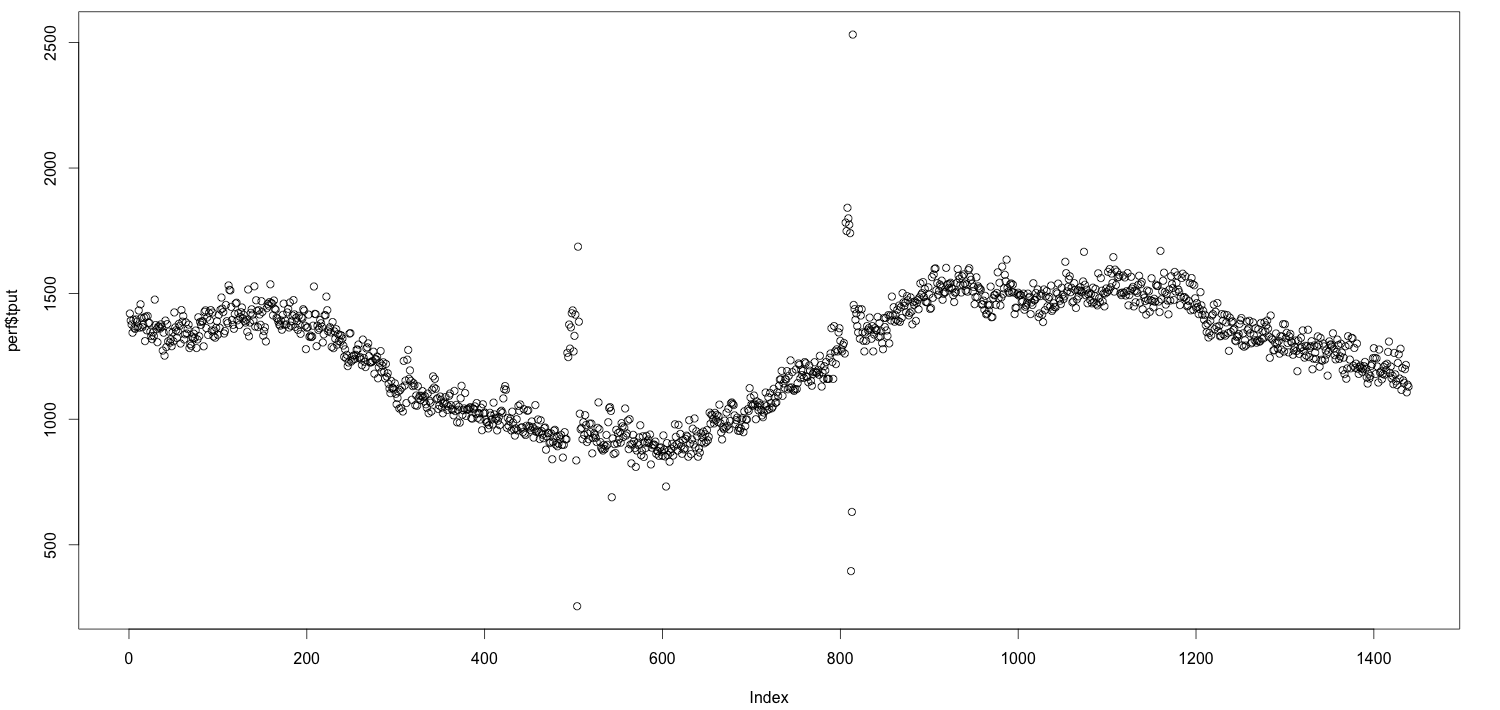
Я не смог найти место, где я видел визуализацию (если вы знаете предшествующий уровень техники ниже, пожалуйста, прокомментируйте!), Поэтому я решил просто написать об этом в блоге. Предположим, вы начинаете с временного ряда:
Идея состоит в том, что вы можете захотеть предупредить об этой метрике, нарушающей некоторый порог, но каково правильное значение? Существует множество способов сделать это: кратное среднего, некоторый квантиль, некоторое стандартное отклонение от среднего значения и т. Д. И т. Д. Например, вы можете сказать: «Я хочу предупредить, если показатель превышает его обычное значение 99,9». процентиль Но разве 99,9 тоже не произвольное число? Что делает его таким особенным? Есть ли какой — нибудь способ , чтобы выбрать номер , который не только вытащил из шляпы?
Мне нужно предварять все это оговоркой. У всех системы разные, статические пороги глупы, квантили в штате Калифорния, как известно, вызывают рак и так далее. То, что я собираюсь показать вам, лишь немного менее произвольно. Не путайте это с правилом, которое на самом деле имеет вескую причину, почему оно лучше, чем альтернативы.
Идея состоит в том, чтобы посмотреть на форму ваших данных и использовать их, чтобы решить, где вы чувствуете, является правильным порогом. «Форма» — это распределение данных — как обычно распределяются их значения.
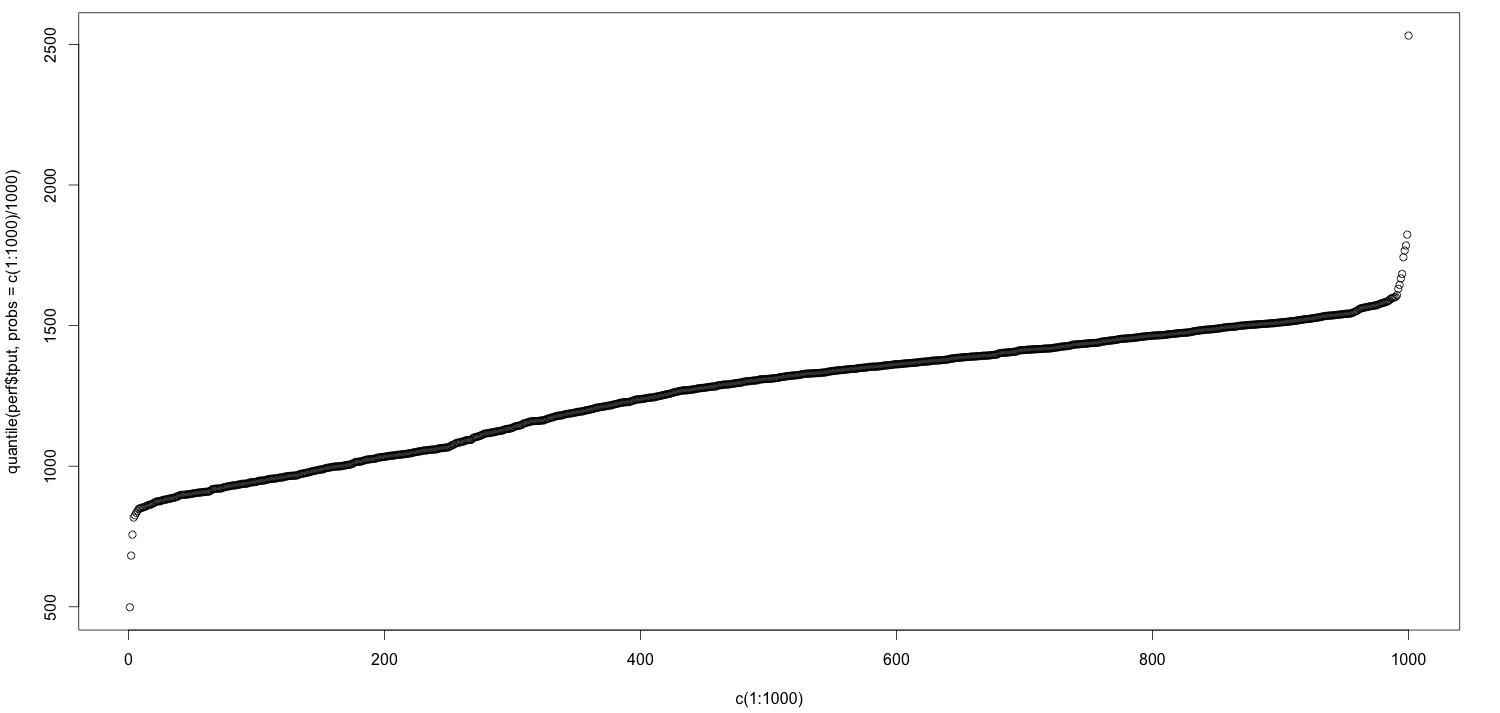
Один из лучших способов сделать это — построить квантили. На следующем графике квантили идут слева направо. В дальнем левом углу находится 0-й процентиль, а в дальнем правом — 100-й процентиль. Другой способ сказать, что слева — это минимальное значение, а справа — максимальное.
Я не пытался оттачивать этот график; вы заметите, что я сгенерировал квантили, взяв вектор из 1000 чисел и разделив его, например, на 1000.
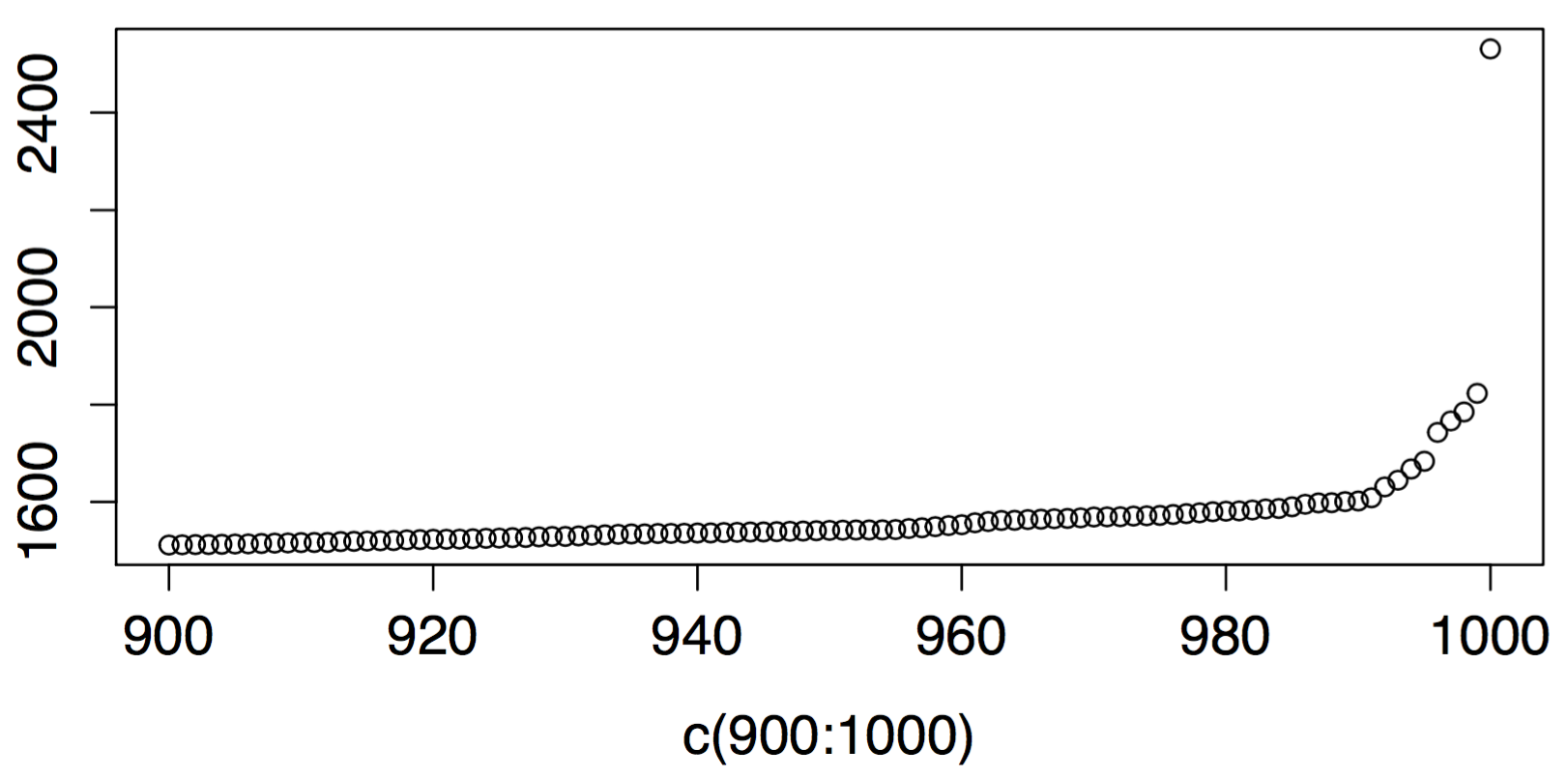
Теперь, когда вы смотрите на этот график, вы видите, что в дальнем правом углу он внезапно прыгает — у него есть локоть. Давайте увеличим последние 10% графика, т.е. 90-й процентиль и выше:
В этом локте нет ничего волшебного. В последних 10 процентах значений нет ничего волшебного. Так уж вышло, что последние несколько непропорционально больше остальных. Проще говоря, это означает, что модель системы или, возможно, параметры ее модели, очевидно, изменились. И если вы собираетесь выбрать место для предупреждения на пороге, возможно, точка, в которой поведение быстро расходится, так же хороша, как и любая, и лучше, чем некоторые.
Другими словами, вы можете поместить свой порог как раз в точку, где квантильный график становится круче, что составляет около 1600 в этом наборе данных.
Не все данные ведут себя таким образом. Некоторые метрики будут иметь красивую линию вверх и вправо, без колена. Некоторые будут прыгать раньше. У некоторых будет большой выступ, даже несколько выступов. Вы получите все виды различных форм и размеров данных. Суть в том, чтобы хотя бы знать, какие формы и размеры имеют ваши собственные данные.
Подобные визуализации имеют много объяснительной силы и могут очень легко показать вам потенциально удивительные вещи. Вот почему этот вид визуализации, а не просто стандартный скучный сюжет временного ряда, неплохо знать, как это сделать. Это не революционно, такие вещи используются многими способами и многими людьми. Графики QQ , например, являются связанной техникой.
Так что я, наверное, повторяюсь слишком много, но опять же, в этом нет ничего особенного, но это все равно что-то. При таком подходе все еще может не быть веского оправдания для выбора числа в качестве порога, но, по крайней мере, есть причина и метод, и он лучше, чем культ груза, генератор случайных чисел или копирование и вставка.
Вот код R
perf <- read.csv("/path/to/perf.csv", sep="")
plot(perf$tput)
plot(c(1:1000), quantile(perf$tput, probs=c(1:1000)/1000))
plot(c(900:1000), quantile(perf$tput, probs=c(900:1000)/1000))
Связанный: кто-то в Твиттере указал мне на этот пост в блоге от Dynatrace .