Во многих случаях при статистическом моделировании мы хотели бы проверить, относится ли базовое распределение из выборки iid к данному (параметрическому) семейству, например, к семейству Гауссов.
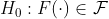
Рассмотрим образец
> library(nortest) > X=rnorm(n)
Тогда естественная идея состоит в том, чтобы использовать качественные тесты соответствия (естественные не обязательно правильные, мы вернемся к этому позже), т.е.
для некоторых 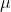
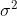
Используя тест Колмогорова-Смирнова, получим
> pn=function(x){pnorm(x,mean(X),sd(X))}; > P.KS.Norm.estimated.param= + ks.test(X,pn)$p.value
Но так как мы выбираем параметры на основе выборки, которую мы используем для запуска теста на соответствие, мы должны ожидать, что где-то возникнут проблемы. Таким образом, другая естественная идея — разделить выборку: первая половина будет использоваться для оценки параметров, а затем мы используем вторую половину для запуска теста на соответствие пригодности (например, с помощью теста Колмогорова-Смирнова)
> pn=function(x){pnorm(x,mean(X[1:(n/2)]), + sd(X[1:(n/2)]))} > P.KS.Norm.out.of.sample= + ks.test(X[(n/2+1):n],pn)$p.value>.05)
В качестве ориентира мы можем использовать тест Лиллифорса, где корректируется распределение статистики Колмогорова-Смирнова, чтобы учесть тот факт, что мы используем оценки параметров
> P.Lilliefors.Norm= + lillie.test(X)$p.value
Здесь давайте рассмотрим iid-образцы размером 200 (здесь было сгенерировано 100 000 образцов). Распределение 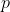
Красный — тест Лиллифорса, где мы видим, что исправление работает хорошо: 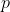
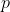
- с помощью теста Колмогорва-Смирнова для всей выборки мы всегда принимаем нормальное предположение (почти) с большим количеством чрезвычайно больших
значений
- с тестом Колмогорва-Смирнова, вне оценки выборки, мы фактически наблюдаем обратное: во многих симуляциях
-значение ниже, чем 5% (с выборкой из
выборки).
Кумулятивная функция распределения 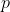
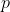
> mean(P.KS.Norm.out.of.sample>.05) [1] 0.85563 > mean(P.KS.Norm.estimated.param>.05) [1] 0.99984 > mean(P.Lilliefors.Norm>.05) [1] 0.9489
Таким образом, использование Колмогорова-Смирнова с оценочными параметрами не является хорошим, так как мы могли бы принять 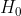
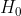
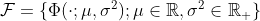
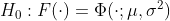
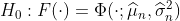

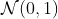 выборки).
выборки).