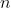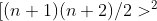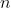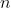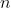Статьи

Таблетки, Полу-таблетки и вероятности

Июль 20, 2018

Вчера я загружал несколько старых постов, чтобы завершить миграцию (я возвращаюсь к своим старым постам, один за другим, чтобы проверить ссылки на картинки, переформатировать R-коды и т. Д.). И я вновь открыл пост, опубликованный почти 2 года назад, о  монахинях и Ангелах Ада в самолете .

Это напомнило мне старую вероятностную проблему (известную как проблема Феймана): Предположим, у вас есть рецепт, чтобы принимать половину таблетки в течение 6 дней. К сожалению, фармацевт был немного ленив (или просто хотел помочь мне написать математическую задачу), и он дает 3 (полные) таблетки в маленькой коробке. В первый день вы принимаете таблетку, разбиваете ее на две части, едите одну и возвращаете другую половину в коробку. На второй день вы случайным образом вытягиваете «что-то» из коробки, то есть либо половину таблетки, либо таблетку. Если это половина первого, то ты ешь это. Если он заполнен, вы разбиваете его на две части, съедаете одну половину и возвращаете другую половину в коробку. И т.д. В День 6, если моя история была хорошо объяснена, вы должны знать, что там может быть только одна половина таблетки. Все идет нормально. Но как насчет 5-го дня? Были либо две половины таблетки, либо одна полная таблетка. Но какова вероятность того, что в день 5 в коробке находилась таблетка для заполнения?

Хорошая проблема, не правда ли?

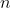
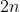
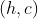
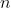
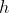
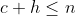
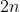
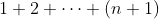
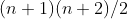
Хорошо, что его можно смоделировать как марковскую модель. Предположим, у нас есть   таблетки. Через   несколько дней коробка будет пуста. Рассмотрим пару,   обозначающую количество половинных таблеток и полных таблеток.  может принимать все значения от 0 до  , и   будет положительным, с  . Таким образом, число государств — возможные пары из 1 -я дня до дня   — будет  , то есть  . Точнее, определить эти состояния в кадре данных,

> n=3
> COMPLETE=HALF=NULL
> for(i in n:0){
+ HALF=c(0:(n-i),HALF)
+ COMPLETE=c(rep(i,length(0:(n-i))),COMPLETE)
+ }
> k=length(COMPLETE)
> state=data.frame(s=1:k,nc=rev(COMPLETE),nh=rev(HALF))
> state
s nc nh
1   1  3  0
2   2  2  1
3   3  2  0
4   4  1  2
5   5  1  1
6   6  1  0
7   7  0  3
8   8  0  2
9   9  0  1
10 10  0  0

Теперь мы можем играть, чтобы вывести матрицу переходов цепи Маркова.

> attach(state)
> P=matrix(0,k,k)
> for(i in 1:k){
+ C=state$nc[i]
+ H=state$nh[i]
+ if((C>0)&(H>0)){
+ P[i,state[(nc==C-1)&(nh==H+1),"s"]]= C/(C+H)
+ P[i,state[(nc==C)&(nh==H-1),"s"]]= H/(C+H)}
+ if((C>0)&(H==0)){
+ P[i,state[(nc==C-1)&(nh==H+1),"s"]]=1}
+ if((C==0)&(H>0)){
+ P[i,state[(nc==C)&(nh==H-1),"s"]]=1}
+ if((C==0)&(H==0)){
+ P[i,state[(nc==C)&(nh==H),"s"]]=1}
+ }

У нас есть матрица переходов (или матрица вероятностей), поскольку все элементы положительны, а сумма на строку равна 1,

> apply(P,1,sum)
[1] 1 1 1 1 1 1 1 1 1 1

Здесь матрица перехода выглядит следующим образом

> P
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,]    0    1 0.00 0.00 0.00  0.0 0.00  0.0    0     0
[2,]    0    0 0.33 0.66 0.00  0.0 0.00  0.0    0     0
[3,]    0    0 0.00 0.00 1.00  0.0 0.00  0.0    0     0
[4,]    0    0 0.00 0.00 0.66  0.0 0.33  0.0    0     0
[5,]    0    0 0.00 0.00 0.00  0.5 0.00  0.5    0     0
[6,]    0    0 0.00 0.00 0.00  0.0 0.00  0.0    1     0
[7,]    0    0 0.00 0.00 0.00  0.0 0.00  1.0    0     0
[8,]    0    0 0.00 0.00 0.00  0.0 0.00  0.0    1     0
[9,]    0    0 0.00 0.00 0.00  0.0 0.00  0.0    0     1
[10,]   0    0 0.00 0.00 0.00  0.0 0.00  0.0    0     1

Чтобы получить нашу вероятность, давайте начнем с состояния 1 — или 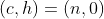  — с вероятностью 1, и давайте посмотрим на распределение в разные периоды,

> dist=c(1,rep(0,k-1))
> MatDist=matrix(NA,2*n+1,k)
> MatDist[1,]=dist
> for(i in 1:(2*n)){dist=as.vector(t(dist)%*%P)
+ MatDist[i+1,]=dist
+ }

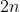
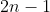
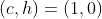
(можно проверить, что через   несколько дней коробка пуста). Вероятность указана в строке  , и мы просто должны проверить, какой столбец соответствует паре  ,

> vs=state[which(MatDist[2*n-1,]>0),]
> proba=MatDist[2*n-1,vs[vs$nc==1,"s"]]
> proba
[1] 0.3888889

Здесь вероятность наличия полной пары в День 5 составляет 38,89%.

На самом деле, можно изучать эволюцию этой вероятности как функция  ,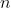

> computeproba=function(n=3){
+ COMPLETE=HALF=NULL
+ for(i in n:0){
+ HALF=c(0:(n-i),HALF)
+ COMPLETE=c(rep(i,length(0:(n-i))),COMPLETE)
+ }
+ k=length(COMPLETE)
+ state=data.frame(s=1:k,nc=rev(COMPLETE),nh=rev(HALF))
+ P=matrix(0,k,k)
+ for(i in 1:k){
+ C=state$nc[i]
+ H=state$nh[i]
+ if((C>0)&(H>0)){
+ P[i,state[(state$nc==C-1)&(state$nh==H+1),"s"]]= C/(C+H)
+ P[i,state[(state$nc==C)&(state$nh==H-1),"s"]]= H/(C+H)}
+ if((C>0)&(H==0)){
+ P[i,state[(state$nc==C-1)&(state$nh==H+1),"s"]]=1}
+ if((C==0)&(H>0)){
+ P[i,state[(state$nc==C)&(state$nh==H-1),"s"]]=1}
+ if((C==0)&(H==0)){
+ P[i,state[(state$nc==C)&(state$nh==H),"s"]]=1}
+ }
+ dist=c(1,rep(0,k-1))
+ MatDist=matrix(NA,2*n+1,k)
+ MatDist[1,]=dist
+ for(i in 1:(2*n)){dist=as.vector(t(dist)%*%P)
+ MatDist[i+1,]=dist
+ }
+ vs=state[which(MatDist[2*n-1,]>0),]
+ proba=MatDist[2*n-1,vs[vs$nc==1,"s"]]
+ return(proba)
+ }

Если мы построим график вероятности как функцию 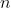 , мы получим

> P=Vectorize(computeproba)(2:40)
> plot(2:40,P,ylim=c(0,.5))

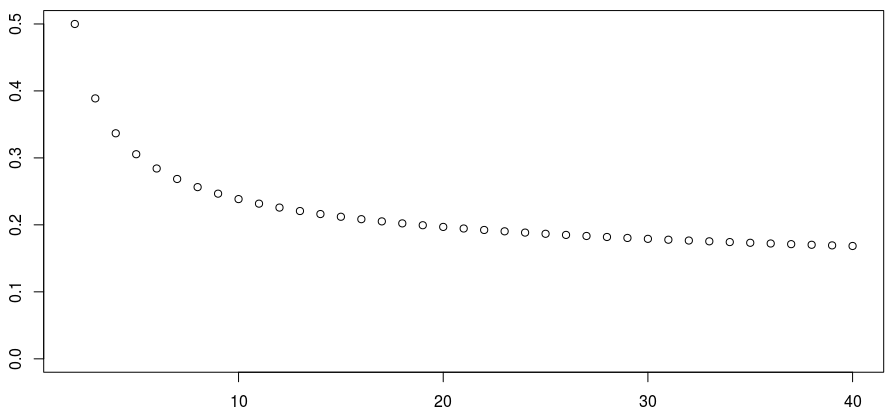
Можно заметить, что вероятность уменьшается. Но медленно, очень медленно. С логарифмической шкалой на оси у мы имеем

> plot(2:40,P,ylim=c(0,.5),log="y")

Если мы посмотрим на «высокие» значения, мы можем получить

> computeproba(100)
[1] 0.14218

Я не знаю, переходит ли этот предел к 0, как   к бесконечности. На самом деле, поскольку нам нужно вычислить матрицу ,   не может быть такой большой … Очень плохо. Если кто-нибудь знает, как эта вероятность ведет себя как функция  , когда   велика, я был бы рад узнать …

35
Share: