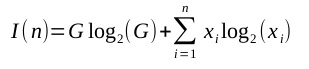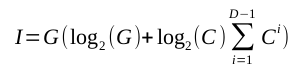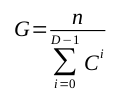Основы
Сколько информации в монетах?
Или в слове «суп»?
Или в броске двух кубиков?
Над такими вопросами размышляли великие умы, среди них блестящий швед Гарри Найквист , за ним следуют американцы Ральф Хартли и — гигант среди гигантов — Клод Шеннон . Их ответы произвели революцию в человеческом мышлении и породили саму информационную теорию .
Теория информации, конечно же, представляет собой огромный интеллектуальный ландшафт, в котором пост в блоге мало что дает. Тем не менее, требуется некоторое введение (благодаря великолепному десятиминутному видео ArtOfTheProblem « Как мы измеряем информацию?» ).
По сути, мы можем оценить информацию о неизвестном количестве, задав ряд вопросов, которые допускают только ответы «да» или «нет». Если кто-то тайно подбрасывает монету, и мы хотим выяснить, приземлилась ли монета на голову или хвост, мы можем задать вопрос: «Это голова?» Каким бы ни был ответ, мы можем выяснить результат, так как даже ответ «нет» подразумевает, что монета должна была упасть на хвосты. Оказывается , что, учитывая количество возможных символов, X , мы можем найти число бит информации в выборе одного символа, взяв базовые два журнал X . Имея два результата, бросок монеты содержит (потому что log 2 (2) = 1 ) один бит информации.
Слово «суп» состоит из четырех букв, каждая из которых выловлена из алфавита из двадцати шести символов. Первый мудрый вопрос, который нужно задать при угадывании какой-либо конкретной буквы — вопрос, который максимизирует эффективность поиска, отбрасывая половину возможных решений, — это «эта буква перед буквой N в алфавите?» Каждый последующий вопрос должен снова половину пространства возможных ответов , так что, в среднем, догадываясь любое письмо будет требовать бревно 2 (26) вопросы. Таким образом, слово «суп» с четырьмя буквами содержит 4 x log 2 (26) = 18,8 бит информации.
Отчаянный игрок, бросающий нормальный шестигранный кубик, делает выбор из шести символов, бросок, содержащий таким образом log 2 (6) битов информации, и бросок двух кубиков, следовательно, содержит 2 x log 2 (6) = 5,2 битов.
Теория информации давно предлагает такие идеи, но можем ли мы пролить свой проницательный луч на исходный код Java? Можем ли мы рассчитать количество информации в структуре программы Java?
Структурная информация.
Рассмотрим следующий элементарный код Java, в котором метод a()имеет зависимости от методов b(), c()и d().
class Test {
void a() {
b();
c();
d();
}
void b() {
System.out.println("Hi from b()");
}
void c() {
System.out.println("Hi from c()");
}
void d() {
System.out.println("Hi from d()");
}
}
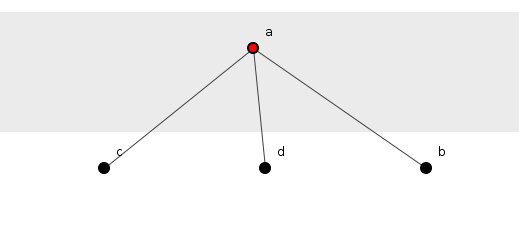
На рисунке 1 этот код изображен как диаграмма спойклина, показывающая зависимости метода, спускающиеся по странице.
Рисунок 1: Метод, вызывающий три других.
Есть ли у этих методов структурная информация? Каков, например, структурный информационный контент метода a()?
Мы могли бы сказать, что структурная информация о методе — это информация, предоставляемая ему в результате его внедрения в структуру в положении, установленном его отношением к другим методам. Структурная информация затем отражает средства, с помощью которых метод относится к другим, в частности альтернативы зависимости, доступные для данного метода при переходе к тем, от которых он зависит.
a()Положение метода в его структуре полностью определяется тем, что он является самым верхним элементом, от которого зависят зависимости от трех других методов системы. Переход от a()следующего метода в структуре включает в себя выбор одной из трех альтернатив, информация, необходимая для этого выбора — с использованием логики, представленной выше — составляет log 2 (3) = 1,58 бит. Поскольку три таких альтернативы открыты a(), то она содержит 3 x 1,58 = 4,75 бит информации.
Ни один из других методов — b(), c()или d()— не допускает навигацию к любой другой, и , следовательно , каждый не содержит никакой информации. Если информация о структуре является суммой информации всех элементов, то вся структура содержит 4,75 бит информации.
Таким образом, в общем случае мы можем вычислить информацию в элементе, умножив количество зависимостей от этого элемента на все остальные на логарифм с двумя основными значениями этого числа зависимостей. Общая информация о n элементах, где i- й элемент имеет зависимости x i от других элементов, определяется как:
(Этот нечетный G log 2 (G) -термин в том, что в противном случае могло бы быть неопределенно- энтропийным уравнением, будет объяснено через мгновение.)
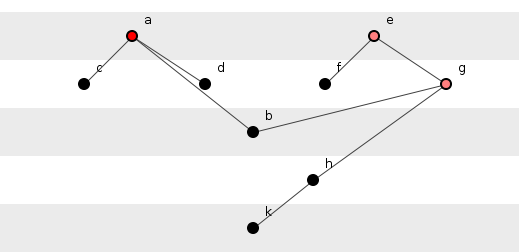
На рисунке 2 показана слегка расширенная версия этой системы, в которой методы, показанные на рисунке 1, оказываются в более благородной борьбе.
Рисунок 2: Две подгруппы методов.
Вычисление информации на фиг.2 происходит непосредственно из анализа на фиг.1, где каждый метод имеет информацию, количественно определенную по количеству его зависимостей, умноженную на лог-число двух оснований этого числа, и с методами, у которых нет зависимостей, не имеющих информации. Действительно, на рисунках приведено цветовое кодирование информационного контента, причем черный цвет обозначает методы без информации, а увеличивающаяся глубина красного цвета обозначает методы увеличения объема информации.
Заслуживают внимания два момента:
Во-первых, метод h()не имеет информации, несмотря на его зависимость от k(). Информационность не ограничивается бездетностью. Целый ряд методов может содержать ровно ноль информации, если он растянут по линии и натянут как струна гитары.
Во-вторых, информация об этой грандиозной системе не может содержаться только в ее методах, потому что, в отличие от рисунка 1, есть два самых верхних метода, то есть два метода, от которых нет никаких зависимостей. Таким образом, информация a()зависит от того, будет ли она выбрана вместо e(): выбор должен быть сделан для выбора между этими двумя методами. Этот выбор генерирует информацию, равную количеству самых лучших методов, умноженному на log-два. Следовательно, G log 2 (G) -термус вышеприведенного уравнения — G — это число самых популярных методов — термин, который обычно доминирует в общем информационном содержании системы.
Эта новая система содержит 10,8 бит информации, что меньше слова «суп».
Информация как Design Cue.
Может ли структурная информация служить основой для разработки лучших программ?
Этот вопрос поднимает понятие эффективности. Инженеры промышленной революции часто объединяли лучшие паровые двигатели, просто повышая эффективность, с которой эти двигатели преобразовывали тепло от сжигания угля в механическую работу. Такая мера может также служить здесь, позволяя программистам оценивать ценность программы по эффективности, с которой программа преобразовала (в некотором смысле) свою информацию в структуру.
Однако есть проблема.
Для обеспечения эффективности система должна учитывать три значения: теоретический минимум, теоретический максимум и фактический максимум, обеспечивая таким образом шкалу, по которой система может калибровать себя. Несмотря на то, что структурная информация действительно дает три таких момента, шкала страдает от непрактичности, поскольку даже небольшие программы выдают потенциально гигантские объемы информации и делают эффективность всех программ неинформативно низкой. (Смотрите здесь для деталей).
К счастью, существуют другие подходы. Одним из таких предложений является создание забавно упрощенной модели структуры исходного кода.
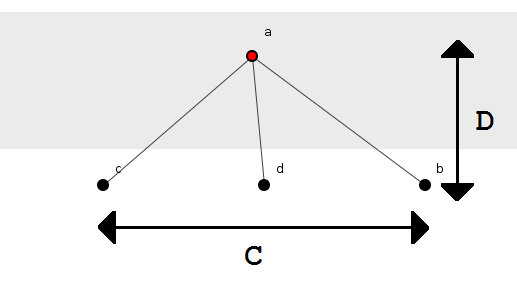
Рассмотрим рисунок 1 еще раз. Это отображает то, что мы будем называть «подгруппой» из четырех методов с методом a()во главе. Подгруппа разделяется на два слоя, определяемых отношениями родитель-потомок и изображаемых горизонтальной полосой. Таким образом, подгруппа составляет два слоя глубоко: метод a(), родитель, сидел один в один слой, методы b(), c()и d(), дети, в другом. Поэтому четыре значения параметризуют эту структуру и составляют модель для исследования: количество методов, n ; количество подгрупп, G ; глубина наслоения, D ; и число детей-методов каждого родителя, C . В случае фигуры 1: n = 4 , G = 1, D = 2 и C = 3 , см. Фиг.3.
Рисунок 3: Небольшая параметризованная система.
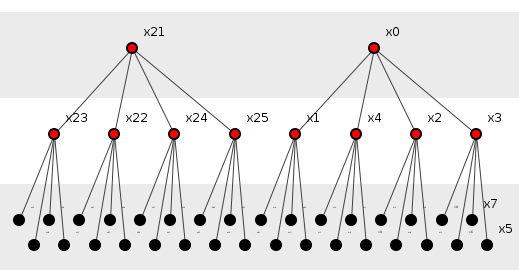
На рисунке 4 показан другой пример, на этот раз из сорока двух методов ( n = 42 ), двух подгрупп ( G = 2 ), трехслойной глубины ( D = 3 ), и каждый родитель имеет четыре дочерних метода ( C = 4). ).
Рисунок 4: Большая параметризованная система.
Эта модель является примером. Это игрушка Его смехотворная регулярность и отсутствие многоэлементных дочерних методов явно делают его нереальным. Однако, несмотря на свои недостатки, модель заключает в себе некоторые особенности реальных программ: реальные программы также объединяются в группы методов, в которых родительские методы порождают несколько дочерних методов, и эти группы часто расширяют поколения. Модель позволяет нам, кроме того, вращать ручки своих четырех параметров и смотреть, как дергающиеся иглы отображают информационное наполнение различных его конфигураций. Документирование тысяч реальных систем для сбора таких данных может занять много времени. Модель обеспечивает такую гибкость, потому что ее четыре параметра переходят в два уравнения (с закрытыми формами), которые дают информацию следующим образом.
Куда:
Эти уравнения, хотя и неаппетитные, говорят нам, что, например, на рисунке 4 описана система из 82 информационных битов.
Конфигурации, они меняются.
Давайте поэкспериментируем на такой игрушечной системе, скажем, 3000 методов. Это фиксирует наш первый параметр, n = 3000 , и оставляет три без ограничений. Три параметра все еще слишком шумные, мы также установим второй параметр и проведем три отдельных эксперимента, в которых последние два будут взаимно изменяться.
Во-первых, давайте сделаем систему поверхностной. Заметно мелко Давайте сделаем это всего три слоя глубиной. Имея эту фиксированную глубину, представим информацию в зависимости от количества детей, см. Рисунок 5.
Рисунок 5: Изменение количества дочерних методов.
На рисунке 5 показано, например, что система из 3000 методов, в которой у «старших» родителей есть трое детей и девять внуков (но не правнуков), обладает информационным содержанием примерно 6000 битов. Система из 3000 методов, в которой у лучших родителей четверо детей и шестнадцать внуков, размахивает около 6500 битов информации и так далее. Абсолютные цифры вряд ли имеют значение: важно то, что информационное содержание системы (после первоначального падения) увеличивается с увеличением числа дочерних методов на одного родителя.
Упрощенно: чем больше детей, тем больше информации .
Информация по существу измеряет количество доступных вариантов выбора при отклонении от конкретного метода. Поскольку наличие большего числа дочерних методов, казалось бы, расширяет любые такие параметры навигации, не удивительно, что наша модель обнаруживает эту первую корреляцию.
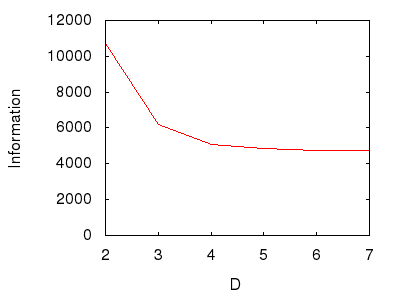
В качестве второго эксперимента, опять-таки с 3000 методов, давайте теперь установим число дочерних методов на три для каждого родителя и вместо этого изменим глубину системы. То есть мы начинаем с системы только родителей и детей (два уровня), затем системы родителей, детей и внуков (три уровня) и т. Д. См. Рисунок 6.
Рисунок 6: Изменение глубины системы.
На рисунке 6 показан противоположный эффект первого эксперимента, а именно то, что с увеличением глубины система теряет информацию. Это может показаться странным, поскольку «чем глубже» система, тем больше путаницы может помешать любой навигации. Но нет, потому что для увеличения глубины системы требуется сделать ее «более узкой» наверху, тем самым обеспечивая все меньше и меньше отправных точек, из которых могут быть получены самые глубокие методы. Эти меньшие начальные выборы перевешивают — по-видимому — увеличивающиеся выборы дальше вниз.
Опять же, упрощенно: чем глубже, тем меньше информации .
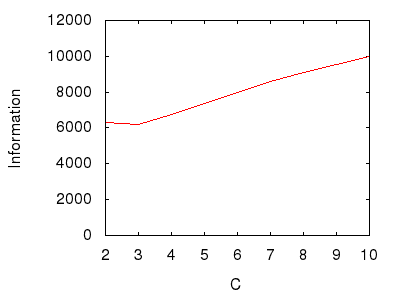
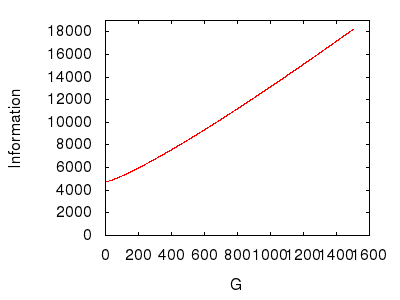
Рисунок 7 принимает другую тактику. Он исследует эффекты подгруппы. Хотя снова фиксируется число дочерних методов на одного родителя в три, вместо этого изменяется количество подгрупп, составляющих систему.
Рисунок 7: Изменение количества подгрупп в системе.
На рисунке 7 показано, что система получает информацию по мере увеличения числа подгрупп. Это наводит на мысль о логике, использованной в предыдущем эксперименте. На рисунке 7, начиная с нескольких подгрупп и добавляя больше, подразумевается, что система расширяется, «Расширяется», и, следовательно, предлагает больше начальных вариантов выбора, с которых начинается навигация по зависимостям. Учитывая фиксированное количество методов, это расширение должно обязательно уменьшить ширину системы, что, в отличие от предыдущего эксперимента, заставляет систему получать информацию.
Итоговая оценка: чем шире, тем больше информации .
Принцип Глубины.
Возникают ли какие-либо закономерности или объединяющие принципы из этих разрозненных результатов?
Ну, может быть.
Принцип глубины считает , что исходный код структура деградирует , как она углубляется, с волновым эффектом вызывает большее опустошение в глубоких структурах , чем в мелком. Вышеуказанные эксперименты предполагают, что глубокие структуры содержат меньше информации, чем мелкие. Следовательно, кажется, что информация коррелирует с поверхностностью, и, следовательно, чем больше информации может похвастать система, тем лучше ее структура.
Это, однако, идет наперекосяк, когда доводится до крайности, поскольку полностью связанные системы (в которых методы зависят от огромного количества других методов) демонстрируют большую часть информации, однако программисты вряд ли будут продвигать идею о том, что системы должны быть полностью связаны.
Возможно, «слишком рано говорить» — это единственный вывод, к которому мы можем прийти на данный момент.
Резюме
Структурная информация пытается измерить степень возможности выбора при переходе от одного метода к другому (или от одного класса к другому, или от одного пакета к другому).
В некоторых других хорошо структурированных системах может существовать корреляция между увеличением информационного содержания и улучшением дизайна.
Но в настоящее время это соотношение остается … незначительным.
Атрибуция фото кредит
CC изображение Без названия любезно предоставлено Gilles k. на Flickr.