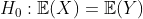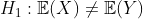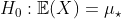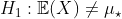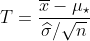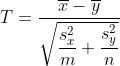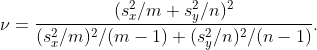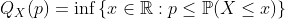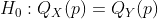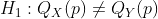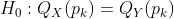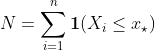Недавно для исследовательской работы у меня было несколько образцов, и я хотел сравнить их. Не для сравнения средств (по построению, все они были в центре), но дисперсия. И не их дисперсия, а скорее их квантили. Рассмотрим следующую boxplot функцию типа, где все квантиль , связанный (что не относится к стандартной boxplot см http://freakonometrics.hypotheses.org/4138 , на французском языке)
> boxplotqbased=function(x){
+ q=quantile(x[is.na(x)==FALSE],c(.05,.25,.5,.75,.95))
+ plot(1,1,col="white",axes=FALSE,xlab="",ylab="",
+ xlim=range(X),ylim=c(1-.6,1+.6))
+ polygon(c(q[2],q[2],q[4],q[4]),1+c(-.4,.4,.4,-.4))
+ segments(q[1],1-.4,q[1],1+.4)
+ segments(q[5],1,q[4],1)
+ segments(q[5],1-.4,q[5],1+.4)
+ segments(q[1],1,q[2],1)
+ segments(q[3],1-.4,q[3],1+.4,lwd=2)
+ xt=x[(x<q[1])|(x>q[5])]
+ points(xt,rep(1,length(xt)))
+ axis(1)
+ }
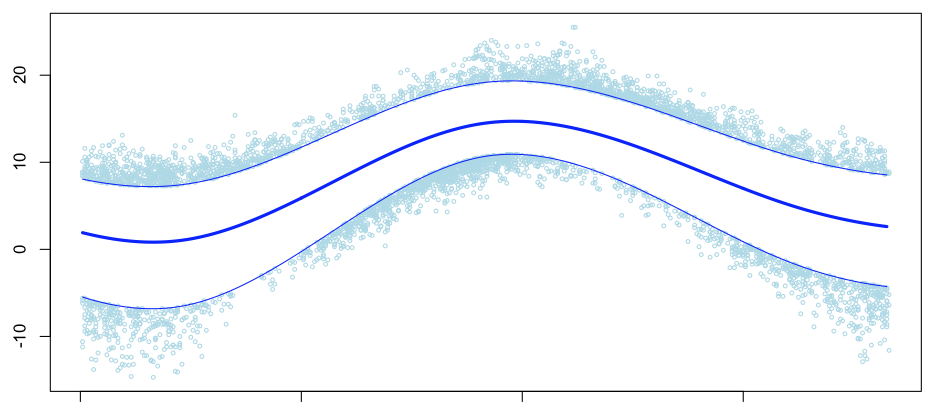
(например, можно легко адаптировать код для списков). Рассмотрим, например, температуру, когда (линейный) тренд удаляется ( обсуждение этой серии в Париже см. Http://freakonometrics.hypotheses.org/1016 ),
с 1 января по 31 декабря. Давайте теперь уберем сезонный цикл, то есть мы имеем здесь разницу со средней сезонной температурой (здесь верхний и нижний квантили),
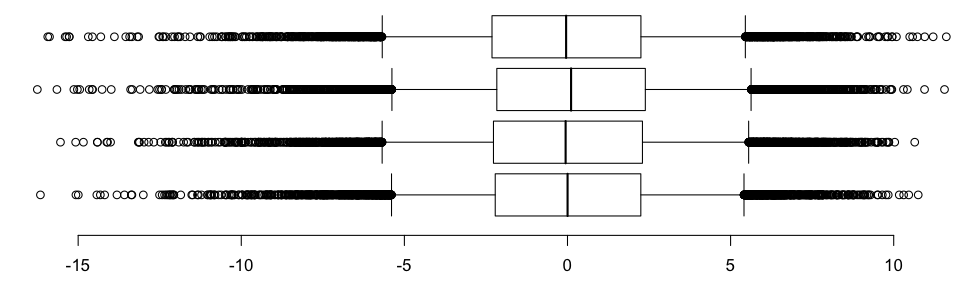
Здесь есть сезонные боксы (осень сверху, лето, весна и зима внизу),
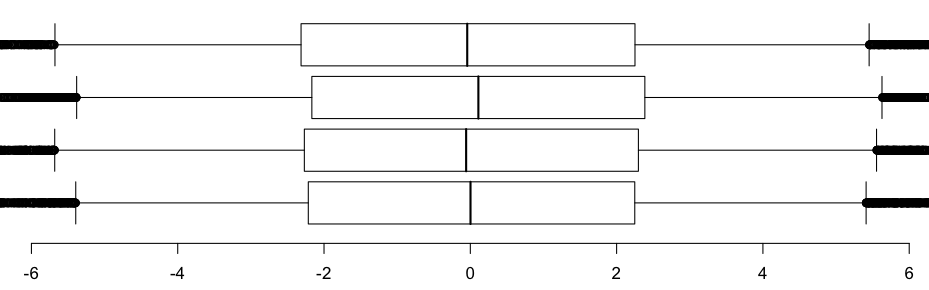
Если мы увеличим масштаб, то получим (где верхний и нижний сегменты представляют собой квантили 95% и 5%, в то время как классически квадраты связаны с квантилями 75% и 25%)
Существует ли (стандартный) тест для сравнения квантилей — возможно, некоторые из них? Можем ли мы легко сравнить квантили, когда есть два (или более) образца?
Обратите внимание, что этот пример по температуре может быть связан с другими старыми сообщениями (см., Например, http://freakonometrics.hypotheses.org/2190 ), но исследовательская работа была посвящена совсем другой теме.
Рассмотрим две (iid) выборки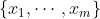 
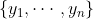
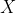
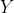
и 
, рассматриваемые как реализации случайных величин 
и 
. Во всех статистических курсах всегда учитываются тесты в среднем, т.е.
против
Обычно идея в курсах состоит в том, чтобы начать с одного образца теста, и проверить что-то вроде
против
Идея состоит в том, чтобы предположить, что выборки из гауссовых переменных,
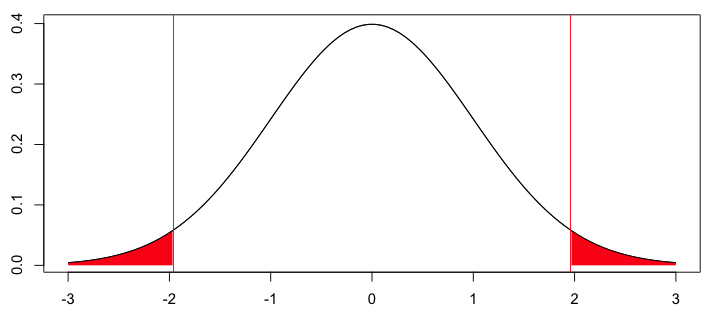
Под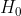 
, 
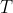
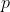
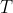
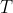
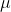
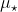
имеет Студенческую т распределение. Все это можно найти в любом курсе «Статистика 101». Мы можем получить 
— значение, вычисление вероятности того, что превышает наблюдаемые значения (для двух односторонних испытаний, вероятности того, что абсолютное значение превышает абсолютное значение наблюдаемой статистики). Этот тест тесно связан с построением доверительных интервалов для 
. Если 
принадлежит доверительный интервал, то это может быть подходящим значением. Графическое представление этого теста связано со следующим графиком
Здесь наблюдаемое значение составило 1,96, то есть значение 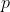— (область, выделенная красным выше) составляет ровно 5%.
Чтобы сравнить средства, стандартный тест основан на
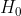
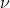
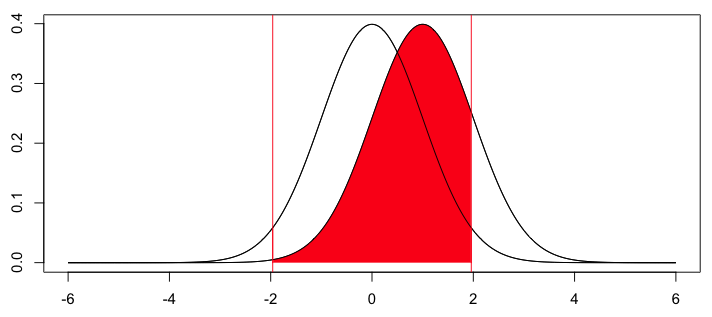
который имеет — под — студент-т распределение со 
степенями свободы, где
Здесь графическое представление следующее,
Но тесты по квантилям редко рассматриваются в статистических курсах. В общем случае определите квантили как
один может быть заинтересованы , чтобы тест 
против 
для некоторых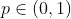 
. Обратите внимание, что нам может быть интересно также проверить,
для всех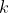 
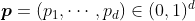
, для некоторого вектора вероятностей 
.
Можно представить, что этот многократный тест будет более сложным. Но более интересным, например, тест на коробочках (равны ли четыре квантиля?). Давайте начнем с чего-то более простого: тест на квантили для одного и того же числа и вывод доверительного интервала для квантилей.
- Квантили для одного образца
Важная идея здесь заключается в том , что она должна быть очень просто получить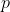 
— значения. Рассмотрим следующий пример, и давайте запустим тест, чтобы оценить, может ли медиана быть нулевой.
> set.seed(1) > X=rnorm(20) > sort(X) [1] -2.21469989 -0.83562861 -0.82046838 -0.62645381 -0.62124058 -0.30538839 [7] -0.04493361 -0.01619026 0.18364332 0.32950777 0.38984324 0.48742905 [13] 0.57578135 0.59390132 0.73832471 0.82122120 0.94383621 1.12493092 [19] 1.51178117 1.59528080 > sum(X<=0) [1] 8
Здесь 8 наблюдений (из 20, то есть 40%) были ниже нуля. Но мы знаем распределение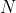 
количества наблюдений ниже цели
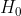
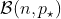
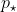
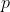
Это биномиальное распределение. В соответствии с этим , это биномиальное распределение, 
где 
находится цель вероятности (здесь 50%, поскольку тест находится на медиане ). Таким образом, можно легко вычислить -значение,
> plot(n,dbinom(n,size=20,prob=0.50),type="s",xlab="",ylab="",col="white")
> abline(v=sum(X<=0),col="red")
> for(i in 1:sum(X<=0)){
+ polygon(c(n[i],n[i],n[i+1],n[i+1]),
+ c(0,rep(dbinom(n[i],size=20,prob=0.50),2),0),col="red",border=NA)
+ polygon(21-c(n[i],n[i],n[i+1],n[i+1]),
+ c(0,rep(dbinom(n[i],size=20,prob=0.50),2),0),col="red",border=NA)
+ }
> lines(n,dbinom(n,size=20,prob=0.50),type="s")
который дает
Здесь 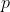-значение
> 2*pbinom(sum(X<=0),20,.5) [1] 0.5034447
Здесь вероятность легко вычислить. Но можно заметить, что здесь есть какая-то асимметрия. На самом деле, если наблюдаемое значение было не 8, а 12, некоторые незначительные изменения должны быть сделаны (чтобы сохранить некоторую симметрию),
> plot(n,dbinom(n,size=20,prob=0.50),type="s",xlab="",ylab="",col="grey")
> abline(v=20-sum(X<=0),col="red")
> for(i in 1:sum(X<=0)){
+ polygon(c(n[i],n[i],n[i+1],n[i+1])-1,
+ c(0,rep(dbinom(n[i],size=20,prob=0.50),2),0),col="red",border=NA)
+ polygon(21-c(n[i],n[i],n[i+1],n[i+1])-1,
+ c(0,rep(dbinom(n[i],size=20,prob=0.50),2),0),col="red",border=NA)
+ }
> lines(n-1,dbinom(n,size=20,prob=0.50),type="s")
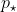
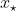
Основываясь на этих наблюдениях, можно легко написать код для проверки, является ли квантиль выборки 
. Или нет. Для двустороннего теста рассмотрим
> quantile.test=function(x,xstar=0,pstar=.5){
+ n=length(x)
+ T1=sum(x<=xstar)
+ T2=sum(x< xstar)
+ p.value=2*min(1-pbinom(T2-1,n,pstar),pbinom(T1,n,pstar))
+ return(p.value)}
Здесь мы имеем
> quantile.test(X) [1] 0.5034447
Теперь, основываясь на этой идее, благодаря двойственности между доверительными интервалами и тестами, можно легко написать функцию, которая вычисляет доверительный интервал для квантилей,
> quantile.interval=function(x,pstar=.5,conf.level=.95){
+ n=length(x)
+ alpha=1-conf.level
+ r=qbinom(alpha/2,n,pstar)
+ alpha1=pbinom(r-1,n,pstar)
+ s=qbinom(1-alpha/2,n,pstar)+1
+ alpha2=1-pbinom(s-1,n,pstar)
+ c.lower=sort(x)[r]
+ c.upper=sort(x)[s]
+ conf.level=1-alpha1-alpha2
+ return(list(interval=c(c.lower,c.upper),confidence=conf.level))}
> quantile.interval(X,.50,.95)
$interval
[1] -0.3053884 0.7383247
$confidence
[1] 0.9586105
Из-за использования неасимптотических распределений мы не можем получить точно 95% доверительный интервал. Но здесь все не так плохо.
- Сравнение квантилей для двух образцов
Теперь сравнить квантили для двух образцов … это сложнее. Точные тесты обсуждаются в Kosorok (1999) (см http://bios.unc.edu/~kosorok/… ) или Li, Тивари и Уэллса (1996) (см http://jstor.org/… ). Что касается вычислительных аспектов, как упоминалось в публикации, опубликованной почти год назад на http://nicebread.de/…, есть функция для сравнения квантилей для двух выборок.
> install.packages("WRS")
> library("WRS")
Здесь можно выполнить несколько тестов на квантилях. Например, по температуре, если мы сравним квантили для зимы и лета (только на 1000 наблюдений, поскольку выполнение этой функции может занять много времени), то есть 5%, 25%, 75% и 95%,
> qcomhd(Z1[1:1000],Z2[1:1000],q=c(.05,.25,.75,.95)) q n1 n2 est.1 est.2 est.1_minus_est.2 ci.low ci.up p_crit p.value signif 1 0.05 1000 1000 -6.9414084 -6.3312131 -0.61019530 -1.6061097 0.3599339 0.01250000 0.220 NO 2 0.25 1000 1000 -3.3893867 -3.1629541 -0.22643261 -0.6123292 0.2085305 0.01666667 0.322 NO 3 0.75 1000 1000 0.5832394 0.7324498 -0.14921041 -0.4606231 0.1689775 0.02500000 0.338 NO 4 0.95 1000 1000 3.7026388 3.6669997 0.03563914 -0.5078507 0.6067754 0.05000000 0.881 NO
или если мы сравним квантили для зимы и лета
> qcomhd(Z1[1:1000],Z3[1:1000],q=c(.05,.25,.75,.95)) q n1 n2 est.1 est.2 est.1_minus_est.2 ci.low ci.up p_crit p.value signif 1 0.05 1000 984 -6.9414084 -6.438318 -0.5030906 -1.3748624 0.39391035 0.02500000 0.278 NO 2 0.25 1000 984 -3.3893867 -3.073818 -0.3155683 -0.7359727 0.06766466 0.01666667 0.103 NO 3 0.75 1000 984 0.5832394 1.010454 -0.4272150 -0.7222362 -0.11997409 0.01250000 0.012 YES 4 0.95 1000 984 3.7026388 3.873347 -0.1707078 -0.7726564 0.37160846 0.05000000 0.539 NO
(затем строятся следующие графики)
 |
 |
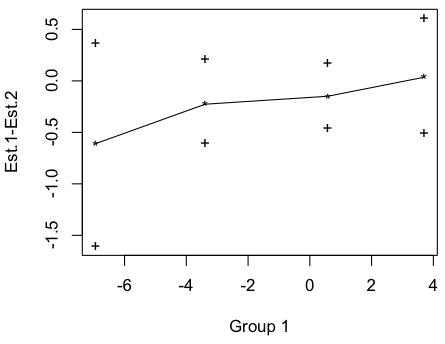Эти тесты основаны на процедуре, предложенной в Wilcox, Erceg-Hurn, Clark and Carlson (2013), онлайн на http://tandfonline.com/… . Они полагаются на использование образцов начальной загрузки. Идея довольно проста на самом деле (даже если в статье они используют оценку Харрелла-Дэвиса для оценки квантилей, то есть взвешенной суммы упорядоченных статистических данных — как описано в http://freakonometrics.hypotheses.org/1755 — но идея может быть понято любым оценщиком): мы генерируем несколько образцов начальной загрузки и вычисляем медиану для всех них (поскольку наш интерес изначально был на медиане)
> Q=rep(NA,10000)
> for(b in 1:10000){
+ Q[b]=quantile(sample(X,size=20,replace=TRUE),.50)
+ }
Затем, чтобы получить доверительный интервал (скажем, с доверительной вероятностью 95%), мы вычисляем квантили этих медианных оценок,
> quantile(Q,c(.025,.975))
2.5% 97.5%
-0.175161 0.666113
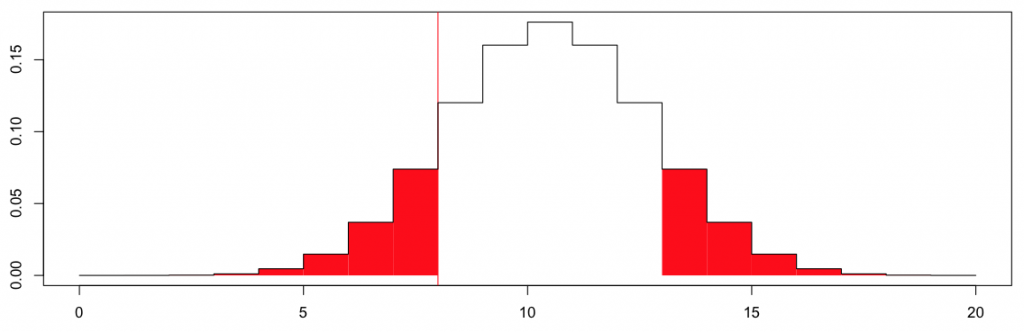
На самом деле мы можем визуализировать распределение этой начальной загрузки,
> hist(Q)
Теперь, если мы хотим сравнить медианы из двух независимых выборок, стратегия довольно схожа: мы загружаем две выборки — независимо — затем вычисляем медиану и учитываем разницу . Тогда посмотрим, будет ли разница существенно отличаться от 0. Например
> set.seed(2)
> Y=rnorm(50,.6)
> QX=QY=D=rep(NA,10000)
> for(b in 1:10000){
+ QX[b]=quantile(sample(X,size=length(X),replace=TRUE),.50)
+ QY[b]=quantile(sample(Y,size=length(Y),replace=TRUE),.50)
+ D[b]=QY[b]-QX[b]
+ }
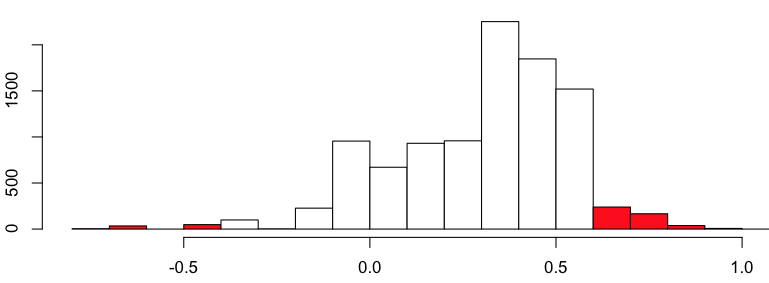
95% доверительный интервал, полученный из разницы начальной загрузки, равен
> quantile(D,c(.025,.975))
2.5% 97.5%
-0.2248471 0.9204888
что довольно близко к, можно получить с помощью функции R
> qcomhd(X,Y,q=.5)
q n1 n2 est.1 est.2 est.1_minus_est.2 ci.low ci.up p_crit p.value signif
1 0.5 20 50 0.318022 0.5958735 -0.2778515 -0.923871 0.1843839 0.05 0.27 NO
(где разница здесь моя противоположность). А при тестировании на 2 (или более) квантилей можно использовать метод Бонферрони, чтобы учесть, что эти тесты нельзя считать независимыми.