Этим утром я работал над некоторым документом о мерах неравенства, и по вычислительным соображениям мне пришлось сортировать элементы в матрице. Чтобы сделать это просто, у меня была прямоугольная матрица, как показано ниже,
> set.seed(1) > u=sample(1:(nc*nl)) > (M1=matrix(u,nl,nc)) [,1] [,2] [,3] [,4] [,5] [,6] [1,] 7 5 11 23 6 17 [2,] 9 18 1 21 24 15 [3,] 13 19 3 8 22 2 [4,] 20 12 14 16 4 10
Пришлось сортировать элементы в этой матрице по строкам.
> (M2=t(apply(M1,1,sort))) [,1] [,2] [,3] [,4] [,5] [,6] [1,] 5 6 7 11 17 23 [2,] 1 9 15 18 21 24 [3,] 2 3 8 13 19 22 [4,] 4 10 12 14 16 20
Приятно, элементы отсортированы по ряду. Но по симметричным причинам я также хотел отсортировать их по столбцам. Итак, из этой отсортированной матрицы я решил отсортировать элементы по столбцам,
> (M3=apply(M2,2,sort)) [,1] [,2] [,3] [,4] [,5] [,6] [1,] 1 3 7 11 16 20 [2,] 2 6 8 13 17 22 [3,] 4 9 12 14 19 23 [4,] 5 10 15 18 21 24
Хорошо, теперь элементы отсортированы по столбцам. Подождите … элементы также отсортированы по строке. Как идет ? Это какое-то совпадение? На самом деле, нет, вы можете попробовать …
> library(scatterplot3d) > nc=6; nl=5 > set.seed(1) > u=sample(1:(nc*nl)) > (M1=matrix(u,nl,nc)) [,1] [,2] [,3] [,4] [,5] [,6] [1,] 8 23 5 30 10 15 [2,] 11 27 4 29 21 28 [3,] 17 16 13 24 26 12 [4,] 25 14 7 20 1 3 [5,] 6 2 18 9 22 19 > M2=t(apply(M1,1,sort)) > M3=apply(M2,2,sort)
> M3
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 1 3 7 14 19 22
[2,] 2 6 9 15 20 25
[3,] 4 8 10 17 23 26
[4,] 5 11 16 18 24 29
[5,] 12 13 21 27 28 30
или используйте следующую функцию, если двух случайных матриц недостаточно,
> doublesort=function(seed=2,nl=4,nc=6){ + set.seed(seed) + u=sample(1:(nc*nl)) + (M1=matrix(u,nl,nc)) + (M2=t(apply(M1,1,sort))) + return(apply(M2,2,sort)) + }
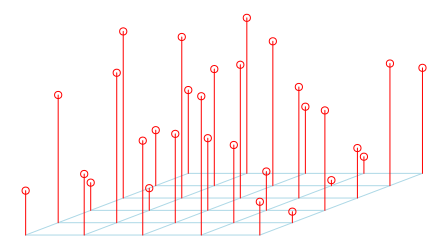
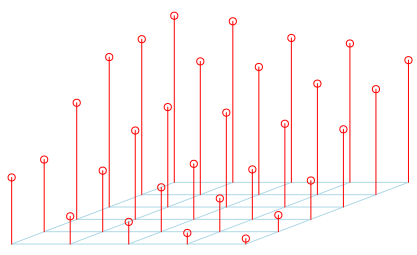
Пожалуйста, не стесняйтесь играть с этой функцией. Потому что так будет всегда. Конечно, это не новый результат. На самом деле, это упоминается в « Больше математических кусочков » Росса Хонсбергера, в связи с какой-то историей о оркестре. Идея проста: возьмем оркестр прямоугольной формы. Вот мои игроки
> library(scatterplot3d) > scatterplot3d(rep(1:nl,nc),rep(1:nc,each=nl), as.vector(M1), + col.axis="blue",angle=40, + col.grid="lightblue", main="", xlab="", ylab="", zlab="", + pch=21, box=FALSE, cex.symbols=1,type="h",color="red",axis=FALSE)
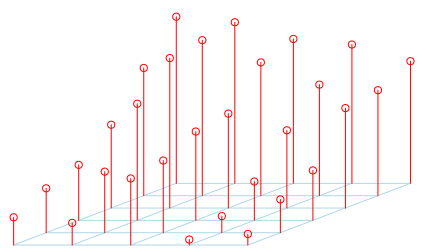
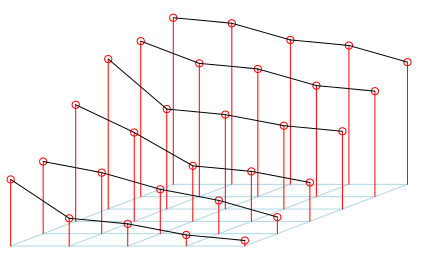
Довольно грязно, не правда ли? По крайней мере, это то, что лидер группы, хотя некоторые высокие игроки прятали более короткие. Таким образом, он вывел более короткие вперед и переместил более высокие сзади. Но все еще на той же линии,
> m=scatterplot3d(rep(1:nl,nc),rep(1:nc,each=nl), as.vector(M2), > col.axis="blue",angle=40, + col.grid="lightblue", main="", xlab="", ylab="", zlab="", + pch=21, box=FALSE, cex.symbols=1,type="h",color="red",axis=FALSE)
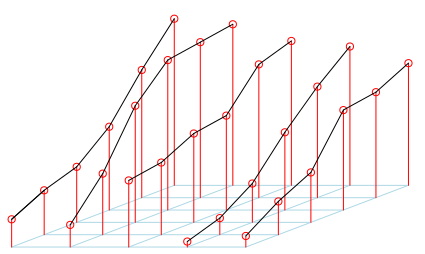
С точки зрения лидера все было хорошо,
> M=M2
> for(i in 1:nl){
+ for(j in 1:(nc-1)){
+ pts=m$xyz.convert(x=c(i,i),y=c(j,j+1),z=c(M[i,j],M[i,j+1]))
+ segments(pts$x[1],pts$y[1],pts$x[2],pts$y[2])
+ }}
Но кто-то из публики (справа от этого графика) не имел такой же точки зрения.
> for(j in 1:nc){
+ for(i in 1:(nl-1)){
+ pts=m$xyz.convert(x=c(i,i+1),y=c(j,j),z=c(M[i,j],M[i+1,j]))
+ segments(pts$x[1],pts$y[1],pts$x[2],pts$y[2])
+ }}
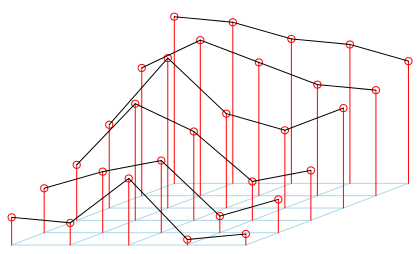
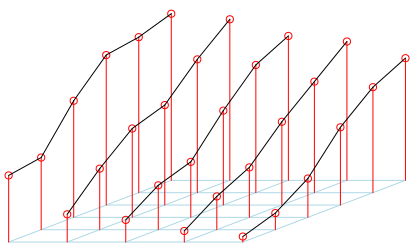
Таким образом, человек в аудитории просит — еще раз — игроков двигаться, но на этот раз, чтобы соответствовать его точке зрения. Поскольку я считаю, что кто-то справа, некоторые незначительные корректировки должны быть сделаны здесь
> sortrev=function(x) sort(x,decreasing=TRUE) > M3b=apply(M2,2,sortrev)
На этот раз намного лучше,
> m=scatterplot3d(rep(1:nl,nc),rep(1:nc,each=nl), as.vector(M3b), + col.axis="blue",angle=40, + col.grid="lightblue", main="", xlab="", ylab="", zlab="", + pch=21, box=FALSE, cex.symbols=1,type="h",color="red",axis=FALSE)
И не только с общественной точки зрения,
> M=M3b
> for(j in 1:nc){
+ for(i in 1:(nl-1)){
+ pts=m$xyz.convert(x=c(i,i+1),y=c(j,j),z=c(M[i,j],M[i+1,j]))
+ segments(pts$x[1],pts$y[1],pts$x[2],pts$y[2])
+ }}
но и для лидера оркестра
Хорошо, не правда ли? И почему это свойство всегда действует? На самом деле, это происходит из теоремы о голубях (еще раз), хорошее объяснение можно найти в книге «Сила голубей » Мартина Гарднера (PDF-версия также доступна на http://www.ualberta.ca/~sgraves. / .. ). Как уже упоминались в конце статьи, есть также интерпретация этого результата , который может быть связан с каким — то волшебным трюком, обсуждение — в картине — несколько месяцев назад на http://www.futilitycloset.com/… : обшивочные карты в любой прямоугольный массив:
Затем поместите каждую строку в числовой порядок:
Теперь поместите каждый столбец в числовой порядок:
Этот последний шаг не нарушил предыдущий: строки все еще в порядке. И это прямой результат из теоремы о голубях . Это круто, не правда ли?