Статьи

Сортировка сетей с использованием функций высшего порядка массива JavaScript

Июнь 13, 2018

Реализация алгоритма сортировки обычно использует один или несколько циклов итерации в форме оператора for / while. С помощью JavaScript и его мощного объекта Array этих циклов можно избежать, потому что функций Array более высокого порядка достаточно для итерации массива. Одним из кандидатов на эту технику является реализация сортировки сетей .

Прежде чем мы начнем, давайте сделаем быстрое обновление некоторых функций высшего порядка. В моем предыдущем посте « Поиск с использованием Array.prototype.reduce» была реализована сортировка вставки без каких-либо операторов цикла. Если мы изменим задачу на сортировку массива чисел, полный код будет:

function sort(entries) {
  return Array.apply(0, Array(entries.length)).map(function () {
    return entries.splice(entries.reduce(function (max, e, i) {
      return e > max.value ? { index: i, value: e } : max;
    }, { value: null }).index, 1).pop();
  }); 
}
 
console.log(sort([14, 3, 77])); // [ 77, 14, 3 ]

Как и типичная сортировка вставки, внешний цикл выбирает наибольшее значение по одному, в то время как внутренний цикл ищет наибольшее число в рабочем массиве. Для внешнего цикла, Array.apply(0, Array(N))это хитрость для генерации пригодного для использования пустого массива, см. Мой другой пост в блоге о Sequence с использованием массива JavaScript . Во внутреннем цикле reduceиспользуется для определения наибольшего числа, а также его индекса. Индекс нужен, чтобы вытащить это число из массива. В то же время число сохраняется в результате сортировки.

Если вы все еще в замешательстве, попробуйте разобрать и отладить приведенный выше код. При необходимости напишите императивную версию, возможно, используя классический цикл for, и сравните обе версии. Это очень полезно понять, чтобы легче было следовать следующей части.

Для сортировочной сети этот процесс состоит из двух этапов. Первым шагом является построение сети компаратора, вторым является фактический процесс сортировки посредством сравнения и обмена в соответствии с построенной сетью. На втором этапе основной операцией является следующая функция (которая действует как блок сравнения):

function compareswap(array, p, q) {
  if (array[p] < array[q]) {
    var temp = array[q];
    array[q] = array[p];
    array[p] = temp;
  }
}

В качестве иллюстрации, если сортируемый массив имеет только 3 числа, практически сортировка будет состоять из следующих шагов:

compareswap(entries, 0, 1); 
compareswap(entries, 1, 2); 
compareswap(entries, 0, 1);

Для 4-значного массива это будет выглядеть так:

compareswap(entries, 0, 1); 
compareswap(entries, 1, 2); 
compareswap(entries, 2, 3); 
compareswap(entries, 0, 1); 
compareswap(entries, 1, 2); 
compareswap(entries, 0, 1);

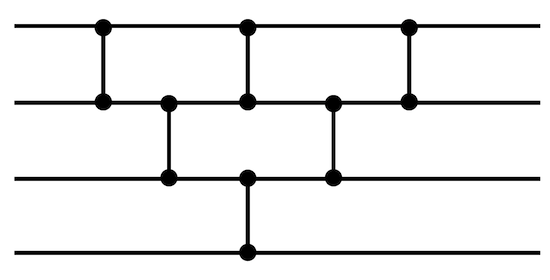
Если мы рисуем последовательность, сортировка аннотации сети выглядит следующим образом. Вы, вероятно, уже можете видеть шаблон здесь, в частности, если вы связываете его с предыдущей реализацией сортировки вставкой. Существует несколько альтернатив для этой конфигурации сетей сортировки, таких как нечетно-четная сортировка слиянием , Bitonic и многие другие.

зп

Сеть компараторов просто формализует это, так что мы можем поместить каждое действие сравнения и обмена в один цикл. Пока у нас есть подходящая сеть для данного размера массива, сортировка является вопросом запуска:

function sort(network, entries) {
  for (var i = 0; i < network.length; ++i)
    compareswap(entries, network[i], network[i] + 1)
}

Тест : что это за алгоритм сортировки?

Как создать сеть? Быстрый способ показан ниже. Обратите внимание, что сеть всегда будет одинаковой для данного размера массива (N), поэтому может иметь смысл запомнить ее в некоторых сценариях.

function createNetwork(N) {
  var network = [];
  for (var i = N - 1; i >= 0; --i)
    for (var j = 0; j < i; ++j)
      network.push(j);
  return network;
}

Очевидно, зачем использовать цикл, если мы можем использовать объект Array? Вот версия из множества других возможностей, в которой используются только функции более высокого порядка Array. Подобно тому, что я обсуждал в построении рядов Фибоначчи , reduceможно (ab) использовать для накопления элементов в массиве, и это служит внешним циклом. Внутренний цикл намного проще, ему нужно только создать последовательность чисел от 0 до текущего предела.

function createNetwork(N) {
  return Array.apply(0, Array(N)).reduce(function (network, _, y) {
    return network.concat(Array.apply(0, Array(N - y - 1)).map(function(_, x) {
      return x;
    }));
  }, []);
}

Сочетание обоих этих двух шагов дает нам окончательный код следующим образом (обратите внимание на тот же шаблон кода для сокращения). Посмотрите, узнаете ли вы конструкцию для каждого шага и сможете ли вы проанализировать, что он там делает.

function sort(input) {
  var array = input.slice(0);
  Array.apply(0, Array(array.length)).reduce(function (network, _, y) {
    return network.concat(Array.apply(0, Array(array.length - y - 1))
      .map(function(_, x) { return x; }));
  }, []).reduce(function(result, p) {
    if (array[p] < array[p + 1]) {
      var temp = array[p + 1];
      array[p + 1] = array[p];
      array[p] = temp;
    }
    return array;
  }, array);
  return array;
}

Хотя сеть сортировки, как предполагается, хорошо подходит для параллельного сравнения, она не дает нам большого преимущества в контексте выше. Однако я надеюсь, что эти два различных способа реализации сортировки в JavaScript вдохновят вас на дальнейшее изучение удивительного мира сетей сортировки.

Примечание . Отдельное спасибо Бэю Чжану за его начальную реализацию сети сортировки и за рецензирование этого поста в блоге.

35
Share: