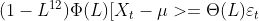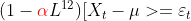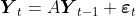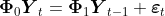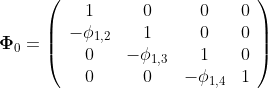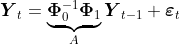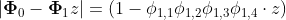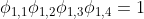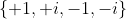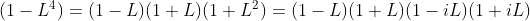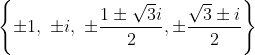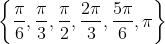Как обсуждалось в курсе MAT8181 , существует, по крайней мере, два вида нестационарных временных рядов: с трендом и с единичным корнем (они будут называться интегрированными ). Тесты единичного корня не могут использоваться для оценки того, является ли временной ряд стационарным или нет. Они могут обнаруживать только интегрированные временные ряды. И то же самое верно для сезонного единичного корня .
В предыдущем посте мы видели, что было трудно моделировать часовую температуру, так как большинство тестов не отклоняют единичные корни. Рассмотрим здесь среднюю месячную температуру, все еще в Монреале, КК.
> montreal=read.table("http://freakonometrics.free.fr/temp-montreal-monthly.txt")
> M=as.matrix(montreal[,2:13])
> X=as.numeric(t(M))
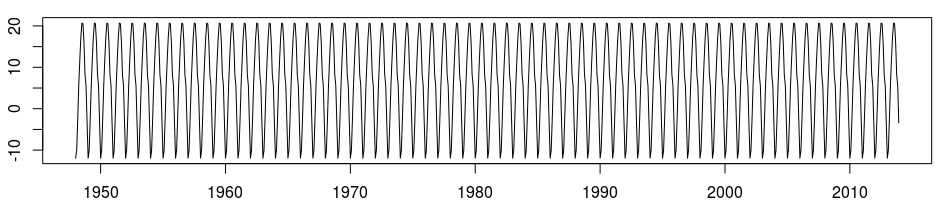
> tsm=ts(X,start=1948,freq=12)
> plot(tsm)
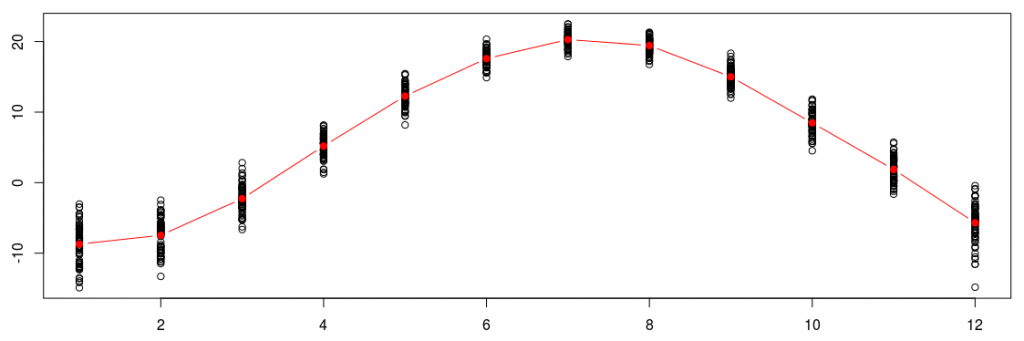
Для тех, кто не знает Монреаль , зима и лето очень разные. Мы можем визуализировать месячные различия, используя
> month=rep(1:12,length(tsm)/12) > plot(month,as.numeric(tsm)) > lines(1:12,apply(M,2,mean),col="red",type="b",pch=19)
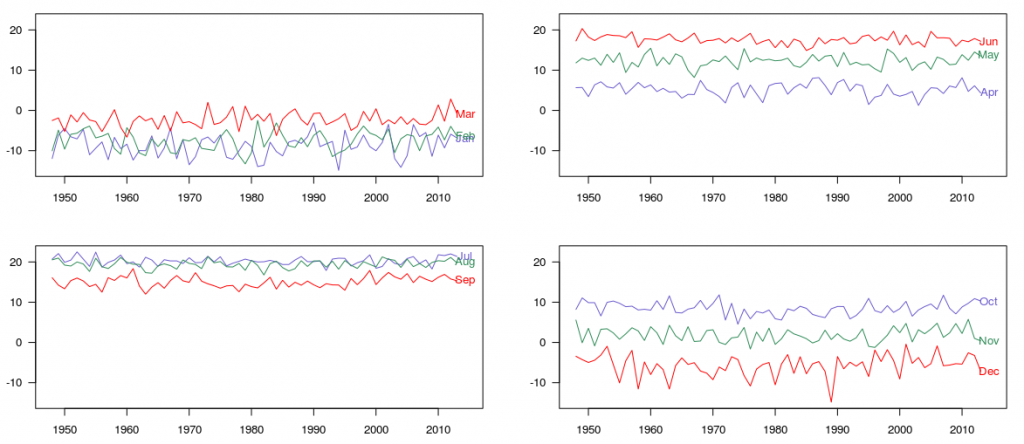
или, если установить пакет uroot , удаленный из репозитория CRAN, мы можем использовать
> library(uroot) > bbplot(tsm)
или же
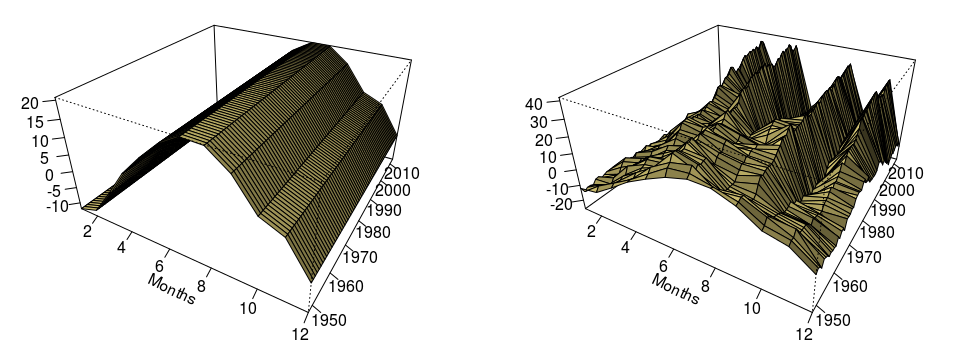
> bb3D(tsm) Loading required package: tcltk
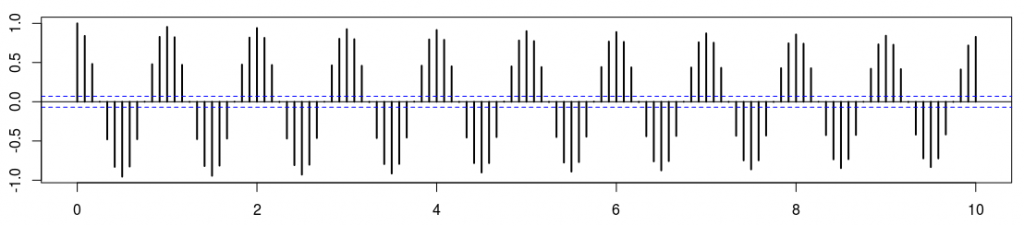
Похоже, наш временной ряд цикличен из-за годовой сезонной модели. Автокорреляционная функция здесь
> acf(tsm,lag=120)
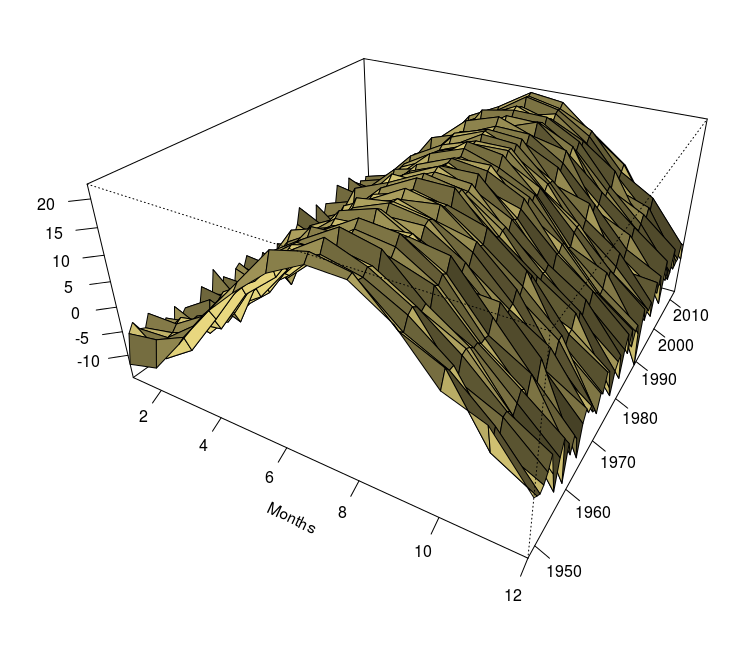
Опять же, этот цикл можно визуализировать, используя
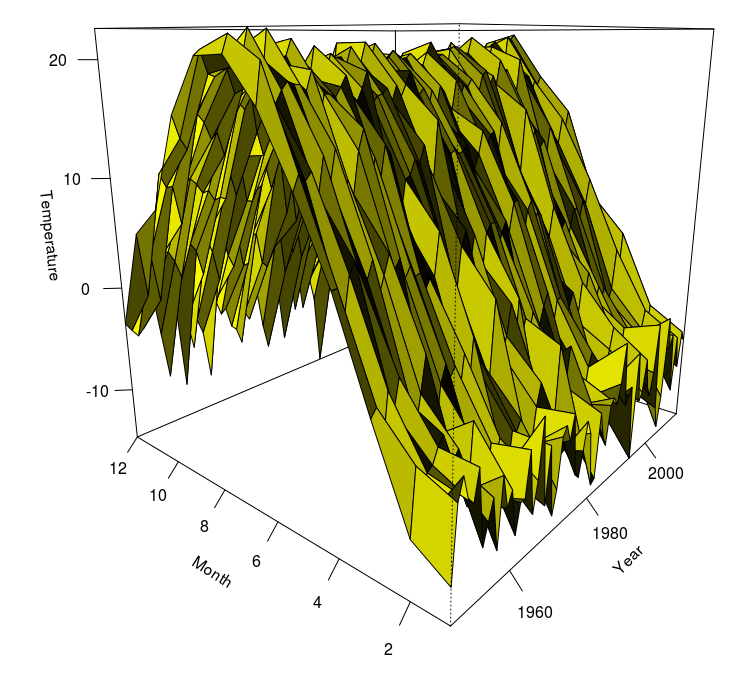
> persp(1948:2013,1:12,M,theta=-50,col="yellow",shade=TRUE, + xlab="Year",ylab="Month",zlab="Temperature",ticktype="detailed")
Теперь вопрос в том, есть ли сезонный единичный корень ? Это будет означать, что наша модель должна быть
Если мы забудем об авторегрессии и компоненте скользящего среднего, мы можем оценить
Если есть корень сезонной единицы, то 
должен быть близок к 1. Так или иначе.
> arima(tsm,order=c(0,0,0),seasonal=list(order=c(1,0,0),period=12))
Call:
arima(x = tsm, order = c(0, 0, 0), seasonal = list(order = c(1, 0, 0), period = 12))
Coefficients:
sar1 intercept
0.9702 6.4566
s.e. 0.0071 2.1515
Это не далеко от 1. На самом деле, это не может быть слишком близко к 1. Если бы это было так, то мы получили бы сообщение об ошибке …
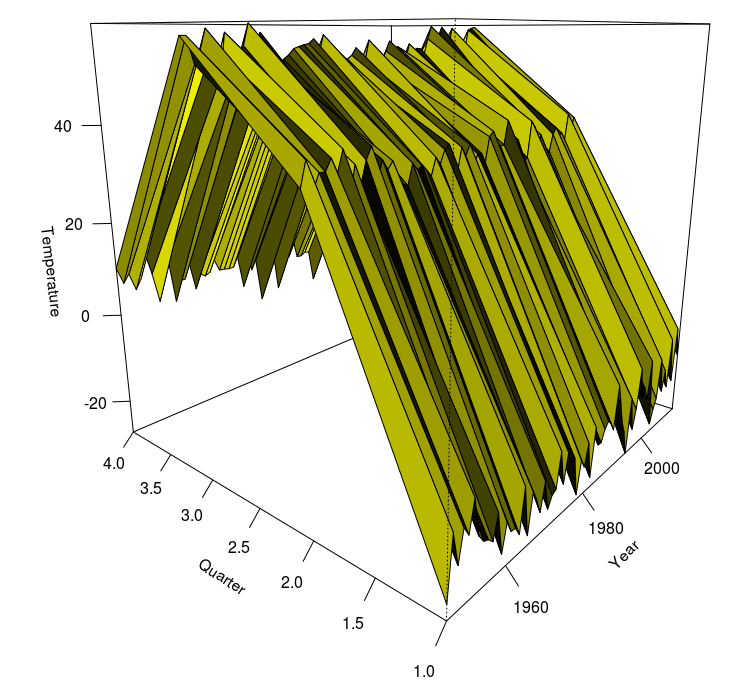
Чтобы проиллюстрировать некоторые интересные модели, давайте рассмотрим также квартальные температуры,
> N=cbind(apply(montreal[,2:4],1,sum),apply(montreal[,5:7],1,sum),apply(montreal[,8:10],1,sum),apply(montreal[,11:13],1,sum)) > X=as.numeric(t(N)) > tsq=ts(X,start=1948,freq=4) > persp(1948:2013,1:4,N,theta=-50,col="yellow",shade=TRUE, + xlab="Year",ylab="Quarter",zlab="Temperature",ticktype="detailed")
(опять же, цель — просто записать некоторые уравнения, если это необходимо)
Почему бы не рассмотреть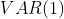 
модель по квартальной температуре? Что-то типа
т.е.
где 
некоторая матрица 
. Эту модель легко оценить,
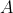
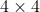
> library(vars)
> df=data.frame(N)
> names(df)=paste("y",1:4,sep="")
> model=VAR(df)
> model
VAR Estimation Results:
=======================
Estimated coefficients for equation y1:
=======================================
Call:
y1 = y1.l1 + y2.l1 + y3.l1 + y4.l1 + const
y1.l1 y2.l1 y3.l1 y4.l1 const
-0.13943065 0.21451118 0.08921237 0.30362065 -34.74793931
Estimated coefficients for equation y2:
=======================================
Call:
y2 = y1.l1 + y2.l1 + y3.l1 + y4.l1 + const
y1.l1 y2.l1 y3.l1 y4.l1 const
0.02520938 0.05288958 -0.13277377 0.05134148 40.68955266
Estimated coefficients for equation y3:
=======================================
Call:
y3 = y1.l1 + y2.l1 + y3.l1 + y4.l1 + const
y1.l1 y2.l1 y3.l1 y4.l1 const
0.07740824 -0.21142726 0.11180518 0.12963931 56.81087283
Estimated coefficients for equation y4:
=======================================
Call:
y4 = y1.l1 + y2.l1 + y3.l1 + y4.l1 + const
y1.l1 y2.l1 y3.l1 y4.l1 const
0.18842863 -0.31964579 0.25099508 -0.04452577 5.73228873
и матрица 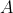здесь
> A=rbind(
+ coefficients(model$varresult$y1)[1:4],
+ coefficients(model$varresult$y2)[1:4],
+ coefficients(model$varresult$y3)[1:4],
+ coefficients(model$varresult$y4)[1:4])
> A
y1.l1 y2.l1 y3.l1 y4.l1
[1,] -0.13943065 0.21451118 0.08921237 0.30362065
[2,] 0.02520938 0.05288958 -0.13277377 0.05134148
[3,] 0.07740824 -0.21142726 0.11180518 0.12963931
[4,] 0.18842863 -0.31964579 0.25099508 -0.04452577
Поскольку стационарные значения этого множества временных рядов тесно связаны с собственными значениями этой матрицы, давайте посмотрим на них,
> eigen(A)$values [1] 0.35834830 -0.32824657 -0.14042175 0.09105836 > Mod(eigen(A)$values) [1] 0.35834830 0.32824657 0.14042175 0.09105836
Похоже, здесь нет проблемы стационарности. Ограниченная модель — это периодическая модель авторегрессии , так называемая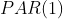 
модель, обсуждаемая Паапом и Франсес.
где
и
Имейте в виду, что это 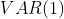модель, так как
Эта модель может быть оценена с использованием определенного пакета (можно также посмотреть на виньетку , чтобы лучше понять синтаксис)
> library(partsm)
> detcomp <- list(regular=c(0,0,0), seasonal=c(1,0), regvar=0)
> model=fit.ar.par(wts=tsq, detcomp=detcomp, type="PAR", p=1)
> PAR.MVrepr(model)
----
Multivariate representation of a PAR model.
Phi0:
1.000 0.000 0.000 0
-0.242 1.000 0.000 0
0.000 -0.261 1.000 0
0.000 0.000 -0.492 1
Phi1:
0 0 0 0.314
0 0 0 0.000
0 0 0 0.000
0 0 0 0.000
Eigen values of Gamma = Phi0^{-1} %*% Phi1:
0.01 0 0 0
Time varing accumulation of shocks:
0.010 0.040 0.155 0.314
0.002 0.010 0.037 0.076
0.001 0.003 0.010 0.020
0.000 0.001 0.005 0.010
Здесь характеристическое уравнение
так что есть (сезонный) единичный корень, если
Что явно не так, здесь. Можно выполнить тест Кановы-Хансена ,
> CH.test(tsq) ------ - ------ ---- Canova & Hansen test ------ - ------ ---- Null hypothesis: Stationarity. Alternative hypothesis: Unit root. Frequency of the tested cycles: pi/2 , pi , L-statistic: 1.122 Lag truncation parameter: 5 Critical values: 0.10 0.05 0.025 0.01 0.846 1.01 1.16 1.35
Идея заключается в том , что полином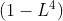 
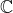
имеет четыре корня, в 
,
поскольку
Если мы вернемся к ежемесячным данным,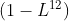 
имеет двенадцать корней,
каждый из них имеет разные интерпретации.
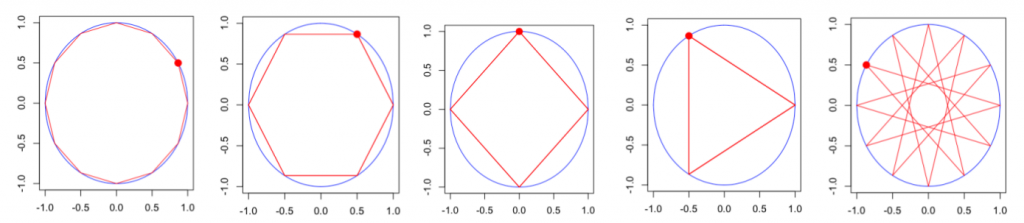
Здесь мы можем иметь 1 цикл в год (на 12 месяцев), 2 цикла в год (на 6 месяцев), 3 цикла в год (на 4 месяца), 4 цикла в год (на 3 месяца), даже 6 циклов в год ( на 2 месяца). Это будет зависеть от аргумента корня, с соответственно
Вывод теста здесь
> CH.test(tsm) ------ - ------ ---- Canova & Hansen test ------ - ------ ---- Null hypothesis: Stationarity. Alternative hypothesis: Unit root. Frequency of the tested cycles: pi/6 , pi/3 , pi/2 , 2pi/3 , 5pi/6 , pi , L-statistic: 1.964 Lag truncation parameter: 20 Critical values: 0.10 0.05 0.025 0.01 2.49 2.75 2.99 3.27
И, похоже, мы отвергаем предположение о сезонном единичном корне. Я могу даже упомянуть следующую процедуру тестирования
> library(forecast) > nsdiffs(tsm, test="ch") [1] 0
где выход: «1» означает, что есть корень сезонной единицы, а «0» — нет корня сезонной единицы. Легко читать, не так ли? Если мы рассмотрим периодическую модель авторегрессии на ежемесячных данных, то результат будет
> model=fit.ar.par(wts=tsm, detcomp=detcomp, type="PAR", p=1)
> model
----
PAR model of order 1 .
y_t = alpha_{1,s}*y_{t-1} + alpha_{2,s}*y_{t-2} + ... + alpha_{p,s}*y_{t-p} + coeffs*detcomp + epsilon_t, for s=1,2,...,12
----
Autoregressive coefficients.
s=1 s=2 s=3 s=4 s=5 s=6 s=7 s=8 s=9 s=10 s=11 s=12
alpha_1s 0.15 0.05 0.07 0.33 0.11 0 0.3 0.38 0.31 0.19 0.15 0.37
Таким образом, независимо от критерия, мы всегда отвергаем предположение о наличии сезонного единичного корня. Что не означает, что у нас не может быть сильного цикла! На самом деле, серия почти периодическая. Но нет единичного корня! Так что все это имеет смысл (я вряд ли верю, что может быть единичный корень — сезонный или нет — в температурах).
Просто чтобы убедиться, что мы правильно поняли, рассмотрим два раза серию, вдохновленную предыдущей. Первая представляет собой периодическую последовательность (с очень очень маленьким шумом, просто чтобы избежать проблемы неопределенных матриц), а вторая четко интегрирована.
> Xp1=Xp2=as.numeric(t(M))
> for(t in 13:length(M)){
+ Xp1[t]=Xp1[t-12]
+ Xp2[t]=Xp2[t-12]+rnorm(1,0,2)
+ }
> Xp1=Xp1+rnorm(length(Xp1),0,.02)
> tsp1=ts(Xp1,start=1948,freq=12)
> tsp2=ts(Xp2,start=1948,freq=12)
> par(mfrow=c(2,1))
> plot(tsp1)
> plot(tsp2)
смотрите также
> par(mfrow=c(1,2)) > bb3D(tsp1) > bb3D(tsp2)
Если мы быстро посмотрим на эти ряды, я бы сказал, что у первого нет корневого элемента — даже если он не является стационарным, но это потому, что ряд является периодическим — в то время как есть (есть?) Корневые (ие) устройства для второй. Если мы посмотрим на тест Кановы-Хансена, мы получим
> CH.test(tsp1) ------ - ------ ---- Canova & Hansen test ------ - ------ ---- Null hypothesis: Stationarity. Alternative hypothesis: Unit root. Frequency of the tested cycles: pi/6 , pi/3 , pi/2 , 2pi/3 , 5pi/6 , pi , L-statistic: 2.234 Lag truncation parameter: 20 Critical values: 0.10 0.05 0.025 0.01 2.49 2.75 2.99 3.27 > CH.test(tsp2) ------ - ------ ---- Canova & Hansen test ------ - ------ ---- Null hypothesis: Stationarity. Alternative hypothesis: Unit root. Frequency of the tested cycles: pi/6 , pi/3 , pi/2 , 2pi/3 , 5pi/6 , pi , L-statistic: 5.448 Lag truncation parameter: 20 Critical values: 0.10 0.05 0.025 0.01 2.49 2.75 2.99 3.27
Я знаю, что этот пакет был удален, поэтому, возможно, мне не следует его использовать. Рассмотрим вместо
> nsdiffs(tsp1, 12,test="ch") [1] 0 > nsdiffs(tsp2, 12,test="ch") [1] 1
Здесь у нас такой же вывод. Первый не имеет единичного корня, но второй имеет. Но будьте осторожны: с тестом Осборна-Чуи-Смита-Бирхенхолла ,
> nsdiffs(tsp1, 12,test="ocsb") [1] 1 > nsdiffs(tsp2, 12,test="ocsb") [1] 1
у нас есть ощущение, что в нашей циклической серии также есть единичный корень …
Так что здесь, на короткой частоте, мы отвергаем предположение о единичном корне — даже о сезонном — в нашем температурном ряду. Когда-нибудь у нас все еще будет проблема с высокой частотой, но, к сожалению, я не думаю, что у меня будет достаточно времени, чтобы ввести зависимость на большие расстояния на этом сеансе.