Несколько месяцев назад я опубликовал пост об отрицательных значениях в треугольниках и о том, как с ними бороться, используя регрессию Пуассона (пост был опубликован на французском языке). Идея заключалась в том, чтобы использовать технику перевода :
- Подогнать модель не на
х, а на
некоторых
,
- Используйте эту модель, чтобы делать прогнозы, а затем переводить эти прогнозы,
Это то, что было сделано, чтобы получить следующий график, где была установлена регрессия Пуассона. Черные точки — 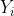
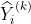
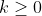
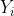
В этом примере не было отрицательных значений, но его можно использовать, чтобы лучше понять влияние этого метода. Здесь прогноз — красная линия. Очевидно, что значение 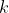
Альтернатива, упомянутая в предыдущем посте, состояла в том, чтобы использовать эту технику в нескольких 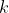
- Для данного
, подобрать модель не на
«s , но на
, что использование модели для прогнозирования, а затем перевести эти предсказания,
.
- Сделай это за несколько
секунд.
- Используйте его, чтобы экстраполировать, когда
есть
(что является интересующим нас случаем).
В контексте резервирования убытков идея предельно проста. Рассмотрим треугольник с пошаговыми выплатами
> source("http://perso.univ-rennes1.fr/arthur.charpentier/bases.R") > Y=T=PAID > n=ncol(T) > Y[,2:n]=T[,2:n]-T[,1:(n-1)] > Y [,1] [,2] [,3] [,4] [,5] [,6] [1,] 3209 1163 39 17 7 21 [2,] 3367 1292 37 24 10 NA [3,] 3871 1474 53 22 NA NA [4,] 4239 1678 103 NA NA NA [5,] 4929 1865 NA NA NA NA [6,] 5217 NA NA NA NA NA
Здесь у нас нет отрицательных значений, но мы все еще можем видеть, могут ли быть использованы методы перевода. Эталоном является регрессия Пуассона, поскольку мы можем запустить ее:
> y=as.vector(as.matrix(Y)) > base=data.frame(y,ai=rep(2000:2005,n),bj=rep(0:(n-1),each=n)) > reg=glm(y~as.factor(ai)+as.factor(bj),data=base,family=poisson)
Здесь сумма резерва представляет собой сумму прогнозируемых значений в нижней части треугольника,
> py=predict(reg,newdata=base,type="response") > sum(py[is.na(base$y)]) [1] 2426.985
что является точной оценкой цепной лестницы.
Теперь давайте воспользуемся техникой перевода для подсчета суммы резервов. Код будет
> decal=function(k){ + reg=glm(y+k~as.factor(ai)+as.factor(bj),data=base,family=poisson) + py=predict(reg,newdata=base,type="response") + return(sum(py[is.na(base$y)]-k))
Например, если мы переведем +5, мы получим
> decal(5) [1] 2454.713
в то время как перевод +10 вернется
> decal(10) [1] 2482.29
Очевидно, что переводы влияют на оценку. Здесь, просто чтобы проверить, если мы не переводим, у нас есть оценка цепной лестницы,
> decal(0) [1] 2426.985
Идея, упомянутая в предыдущем посте, состояла в том, чтобы попробовать несколько переводов, а затем экстраполировать, чтобы получить значение в 0. Здесь переводы дадут следующие оценки
> K=10:20 > (V=Vectorize(decal)(K)) [1] 2482.290 2487.788 2493.279 2498.765 2504.245 2509.719 2515.187 2520.649 [9] 2526.106 2531.557 2537.001
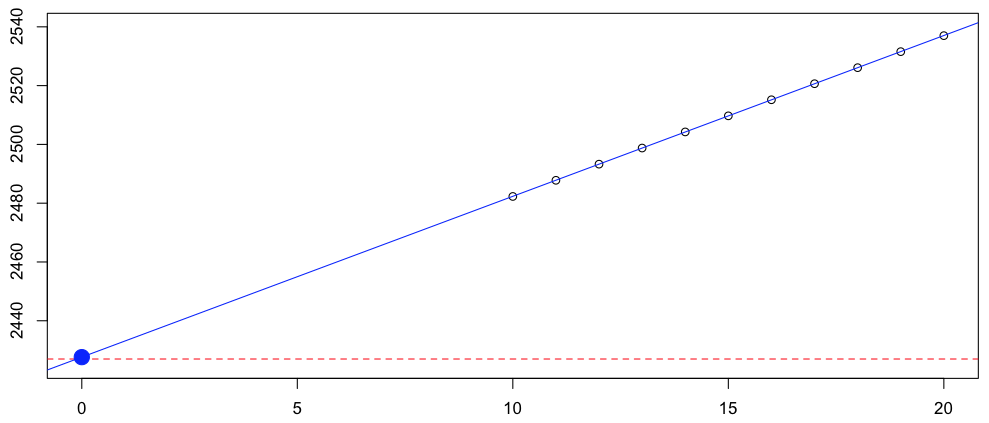
Мы можем построить эти значения и запустить регрессию
> plot(K,V,xlim=c(0,20),ylim=c(2425,2540)) > abline(h=decal(0),col="red",lty=2)
пунктирная горизонтальная линия — цепная лестница. Теперь давайте экстраполируем
> b=data.frame(K=K,D=V) > rk=lm(D~K,data=b) > predict(rk,newdata=data.frame(K=0)) 1 2427.623
Он должен признать, что это не так уж плохо. Но вчера вечером Карим спросил меня, почему я использовал линейную регрессию для моей экстраполяции. И если честно, я не знаю. Я имею в виду, единственный ответ может быть, что точки почти на прямой линии. Поэтому, когда я впервые увидел это, я был взволнован и запустил линейную регрессию.
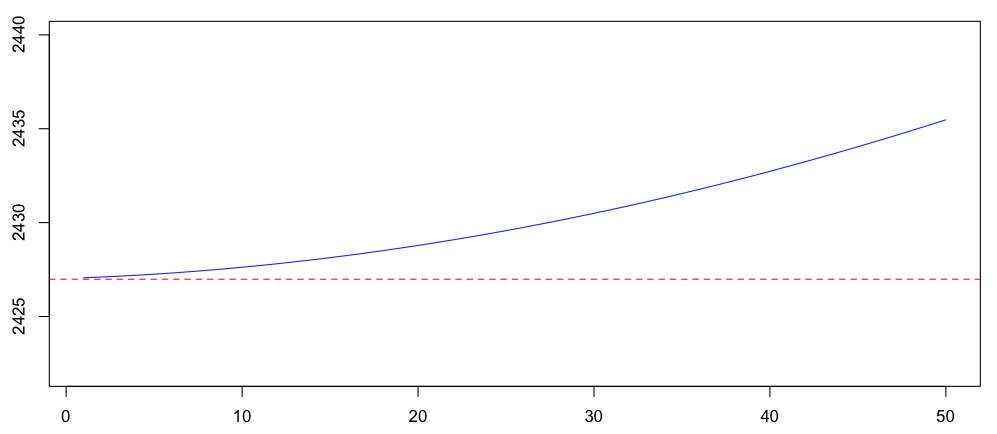
Теперь давайте посмотрим, сможем ли мы сделать лучше. Потому что здесь мы используем перевод +10 или +20 (который может быть довольно маленьким). Что если мы используем гораздо большие значения? (потому что у нас могут быть большие отрицательные инкрементные значения). С помощью следующего кода мы пытаемся каждый раз 11 последовательных значений, наименьшее из которых идет от 0 до 50,
> hausse=1:50; res=rep(NA,50) > for(k in hausse){ + VK=k:(10+k) + b=data.frame(K=VK,D=Vectorize(decal)(VK)) + rk=lm(D~K,data=b) + res[k]=predict(rk,newdata=data.frame(K=0)) + } > plot(hausse,res,type="l",col="red",ylim=c(2422,2440)) > abline(rk,col="blue")
Здесь мы вычисляем резервы, когда экстраполяции были сделаны после 11 переводов, с 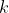
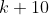
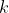
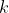
> res[hausse==10] [1] 2427.623
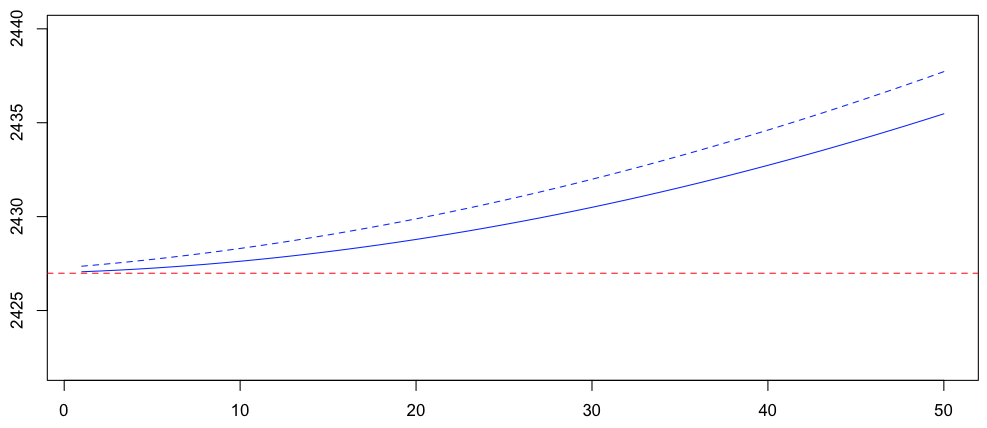
На самом деле, также возможно рассмотреть не 11 переводов, а 26, от 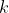
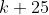
> hausse=1:50; res=rep(NA,50) > for(k in hausse){ + VK=k:(25+k) + b=data.frame(K=VK,D=Vectorize(decal)(VK)) + rk=lm(D~K,data=b) + res[k]=predict(rk,newdata=data.frame(K=0)) + } > lines(hausse,res,type="l",col="blue",lty=2)
Теперь у нас есть пунктирная линия
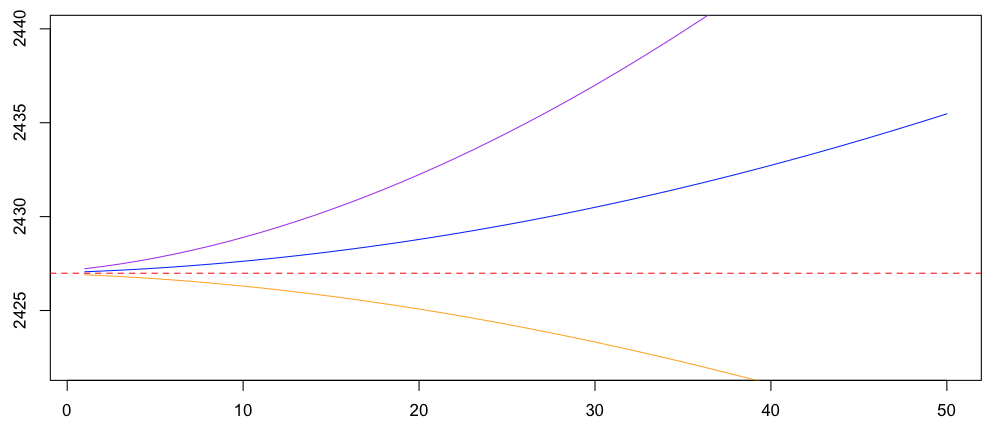
Здесь становится хуже. Итак, давайте оставим здесь 11 переводов. Возможно, мы можем попробовать что-то другое. Например, регрессия Пуассона с логарифмическим выражением (т.е. мы рассматриваем экспоненциальную экстраполяцию),
> hausse=1:50; res=rep(NA,50) > for(k in hausse){ + VK=k:(10+k) + b=data.frame(K=VK,D=Vectorize(decal)(VK)) + rk=glm(D~K,data=b,family=poisson) + res[k]=predict(rk,newdata=data.frame(K=0),type="response") + } > lines(hausse,res,type="l",col="purple")
Фиолетовая линия — это модель Пуассона со ссылкой на журнал. Возможно, мы можем попробовать другую функцию связи, например, квадратичную
> hausse=1:50; res=rep(NA,50) > for(k in hausse){ + VK=k:(10+k) + b=data.frame(K=VK,D=Vectorize(decal)(VK)) + rk=glm(D~K,data=b,family=poisson(link= + power(lambda = 2))) + res[k]=predict(rk,newdata=data.frame(K=0),type="response") + } > lines(hausse,res,type="l",col="orange")
Это была бы оранжевая линия,
Здесь нам нужна функция связи между тождеством (линейная модель, синяя линия) и квадратичной (оранжевая), например, степенной функцией 3/2,
> hausse=1:50; res=rep(NA,50) > for(k in hausse){ + VK=k:(10+k) + b=data.frame(K=VK,D=Vectorize(decal)(VK)) + rk=glm(D~K,data=b,family=poisson(link= + power(lambda = 1.5))) + res[k]=predict(rk,newdata=data.frame(K=0),type="response") + } > lines(hausse,res,type="l",col="green")
Здесь, похоже, мы можем использовать эту модель для любого вида перевода, от +10 до +50, даже +100! Но у меня нет никакой интуиции об использовании этой функции власти …
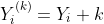 некоторых
некоторых 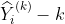

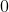 (что является интересующим нас случаем).
(что является интересующим нас случаем).